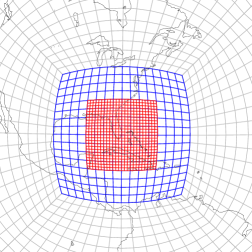
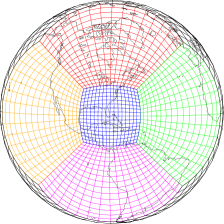
Lucas Harris is working on methods for locally increasing model resolution in the atmospheric dynamical core. The two primary methods for doing this are grid nesting and grid stretching. These techniques will allow the GFDL atmospheric model to be run at a very high resolution over a limited area for use in hurricane forecasting, long-range chemical transport, seasonal prediction, and regional climate modeling.
Grid nesting is very common in mesoscale and limited-area modeling but is not often used in global modeling. A nested grid is a model grid which covers a smaller area than its ‘parent’ or coarse grid but has a smaller grid spacing, allowing for smaller scale features to be better resolved. The boundary conditions for the nested grid are then formed from coarse-grid data, a procedure for which few satisfactory methods are known to exist. The nested-grid data can then feed back onto the coarse grid through ‘two-way’ nesting, in which the coarse-grid solution is periodically replaced with that on the nested grid. This procedure allows for nested-grid disturbances to influence their large-scale environment, which is necessary for simulating hurricanes, and may also cause smaller reflections at the boundary of the nested grid than if there were no feedback.
Grid stretching is less commonly used than grid nesting, but holds some advantages over nesting. The primary benefits of a stretched grid are the lack an abrupt change in grid resolution that can cause reflections and not requiring special procedures for boundary conditions or two-way feedback. The cubed-sphere geometry of the GFDL atmospheric dynamical core is particularly suited for grid stretching as one face can be continuously transformed to cover a given small area of the earth’s surface while retaining a regular quadrilateral grid that only gradually increases its grid spacing across a cube edge.
For either grid stretching or nesting it is important to have accurate boundary or cube-edge handling to avoid distortion of the flow and a general increase in error. Further it is necessary for long-term simulations to conserve mass, and the boundary conditions must be formulated to take this into account.