Rotating and non-rotating horizontally homogeneous convecting atmospheres
Comprehensive climate models are extremely complex dynamical systems, and there is a clear need for a variety of simpler models to help us understand nature and help us understand our comprehensive climate models. Click here for an essay on the importance of a hierarchy of models of differing levels of complexity .
One approach to idealization is to remove the complications of the Earth’s spherical geometry and its complex inhomogeneous surface, and instead consider a horizontally homogeneous planar domain. Horizontally homogeneous in this context implies that each horizontal location is physically identical to every other location. This is traditionally achieved by studying doubly-periodic domains (as one leaves one side of the domain, one enters the other side.) A rotating system can be approximated by adding the Coriolis force, still retaining horizontal homogeneity.
To study the tropical climate, one can study radiative-convective equilibrium in such a doubly periodic box. Typically, one fixes the surface temperature and assumes that the surface is water-saturated (mimicking conditions over the ocean). One then turns on the Sun, evaporates water, and allows the model fluid dynamics, radiation, and thermodynamics to redistribute energy and generate a hydrological cycle with precipitation balancing evaporation. One may be interested in how the relative humidity or cloud distributions are maintained in such an ideallized horizontally homogeneous system, or one may focus on the (related) question of the how the convection is organized. Moist convection, dominated by phase changes, has many strange and unfamiliar aspects that are usefully isolated in these idealized geometries. One of the first simulation of radiative-convective equilibrium, and (to our knowledge) the first with radiation fully interactive with the model-generated clouds (albeit with one horizontal dimension only), was produced at GFDL in 1993.
We have recently considered a special case of this kind of model in which we take our comprehensive atmospheric model, and simplify the geometry to create a homogeneous model of radiative-convective equilibrium, while still retaining all of the parameterizations in the full model, meant to represent sub-grid scale processes. The goal here is primarily to better understand the global model. We have performed simulations with non-rotating and rotating systems.
The results from the rotating case where surprising, in that the domain would fill up with closely packed tropical storms for all of the cases that we examined. The global model, which differs only in its inhomogeneous spherical geometry, produces relatively few storms, so the inhomogeneities in the global model are actively suppressing storm genesis.
The storms that live in this homogeneous environment typically survive for hundreds of days and rarely, if every merge. This is a distinctive kind of geophysical turbulence that is vortex-dominated but strongly dissipative (if one eliminates the evaporation, the storms decay in a few days). This system provides a new tool to study the tropical storm-like vortices generated in global models.
We hope to perform similar simulations at much higher resolution, without the subgrid parameterizations used here,
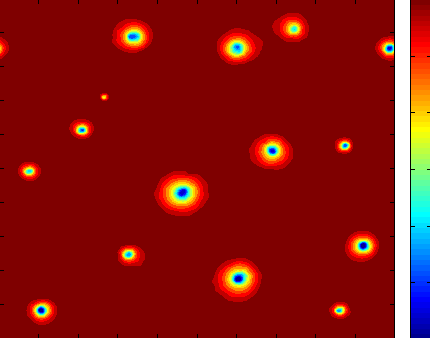
Surface pressure in a simulation of rotating radiative convective equilibrium
as described by Held and Zhao, showing how the doubly-periodic domain is filled with tropical storms.
The grid size in 50km and the domain size is 20,000 x 20,000 km.
For more information, please contact Isaac Held (Isaac.Held@noaa.gov)


