Ice-ocean interactions

Contacts, for more information:
The largest mass loss from both Greenland and Antarctic ice sheets is observed at their margins, in areas where warm ocean waters have access to outlet glaciers and ice shelves. Migration of the grounding line (the boundary between floating ice and ice grounded on bedrock), and changes in ice flux through it, result in variations of ice-sheet contributions to sea level. The ongoing changes in the Amundsen Sea Embayment (Antarctica) – increased mass loss, retreat of the grounding line, acceleration of the grounded ice streams feeding floating ice shelves and ice tongues – are attributed to either the direct or indirect effects of the oceans.
Ice shelves and surrounding oceans mutually affect each other. On the oceanographic side, ice shelves provide a surface boundary condition that is different than open ocean or sea ice, with water subject to a depth-dependent freezing point and relatively large gradients in surface hydrostatic pressure. The induced submarine melting and freezing and density-driven circulation affect nearby seawater properties. On the glaciological side, the ice shelves control ice mass flux through the grounding line. Understanding these mutual effects is paramount for reliable projections of ice discharge from the continental ice sheets into oceans and for robust attributions of the observed changes.
GFDL Research
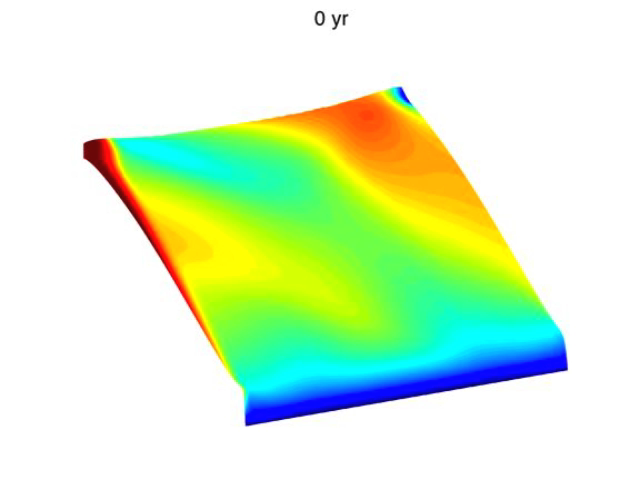
Coupled Ice-shelf/sub-ice-shelf-cavity system
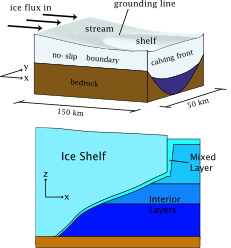
Figure 1 Geometry of the coupled ice-stream-shelf-cavity system. Top image is 3d view, bottom image is a longitudinal cross-section
Investigations of the mutual effects of ice shelves and surrounding oceans, as well as the effects of changes in oceanic environments on the grounded ice require a new breed of models – fully coupled ice-ocean models. There are a number of challenges in developing such models. Examples of these challenges include evolving geometries of sub-ice-shelf cavities and moving boundaries between different model components (migration of the grounding line), drastically different characteristic timescales of the ocean circulations (order of days to years) and ice flow (order of decades to centuries).
A three-dimensional ocean model (GOLD), coupled to a two-dimensional (top view) dynamic ice shelf- ice stream model capable of resolving grounding line migration, has been developed to assess the effects of coupling and investigate sensitivities of the coupled system. The model simulations suggest the presence of distinct patterns of adjustment, spanning multiple timescales. The ice shelf was seen to adjust on the decadal scale, initially thinning and steepening near the grounding line, then thinning further downstream due to melting in a rotationally induced ocean boundary current, as well as due to advection of upstream thinning.
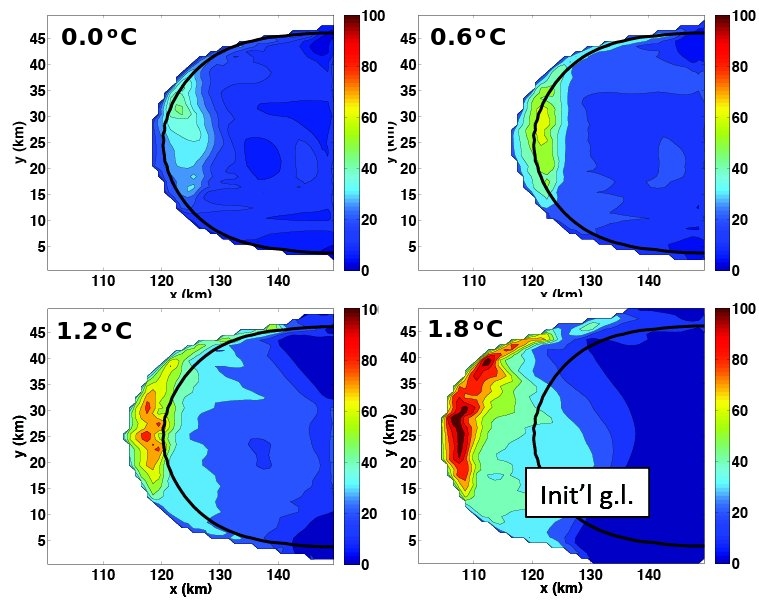
Figure 2 Sensitivities of the coupled system to the far-field ocean temperature. Color shows melt rates, black lines show initial location of the grounding line
The melt rate field, controlled strongly by ice shelf geometry as well as background stratification, changed considerably over this time. It became both more concentrated near the grounding line and developed higher melt rates within and near the outflowing boundary current. The modification of the ice shelf geometry led to grounded ice thinning and grounding line retreat through stress field modification. This stress imbalance was eventually offset, on a much longer timescale, by ice shelf lengthening (due to grounding line retreat with a fixed calving front).
Investigations of sensitivity of the coupled ice-shelf/sub-ice-shelf cavity system to different far-field oceanic temperatures ranging between 0 and 1.8oC show that ocean temperature has a strong effect on sub-ice shelf melt rates, ice shelf geometry, and grounded ice response.
Melt rates and ice shelf morphology differed in their response from that of grounded ice. As temperature increased (by constant increments), the corresponding increase in terms of maximum melt rate and ice shelf basal slope was relatively constant. In contrast, loss of grounded ice showed a much stronger increase at the highest temperature forcing. In the long term (century scale), the strong response at high temperature forcing was likely due to concentrated melting and thinning in an area of the shelf that is important to the shelf’s buttressing.
Ice-shelf/ocean-wave interactions
Ice shelves experience continuous impact of ocean waves. The waves that affect ice shelves range from short-period sea swell to very long period waves formed by large storms and cyclones in distant oceans. As the waves reach ice shelves they produce mechanical impact: they force floating ice to flex. Continuous ice flexing and bending make small fractures that evolve into crevasses that can propagate through the whole depth of ice shelves and eventually form icebergs.
Modeling studies performed at GFDL suggest that short-period sea swell affects ice-shelf areas close to the ice fronts. Meanwhile, long-period ocean waves can propagate into ice-shelf cavities reaching their grounding lines and excite ice-shelf flexural gravity waves that affect the interior of ice shelves far away from their ice fronts. The results of these studies revealed that these flexural gravity waves propagate as narrow concentrated beams, which direction is determined by the incident ocean waves and the width is determined by the period of the incident ocean waves. In some instances when frequencies of incident ocean waves are close to the ice-shelf eigenfrequencies, the ocean waves can excite normal-mode oscillations in ice shelves.
Interactions of ice shelves with cold and warm oceanic environments
Antarctic ice shelves exist in a variety of oceanographic thermal regimes: from “cold” regime exemplified by the Filchner-Ronne and Ross ice shelves, where the sub-ice shelf water is dominated by high-salinity shelf water at ~1.8oC, to “warm” regime exemplified by the Pine Island Glacier or George VI ice shelves, where the sub-ice shelf water is dominated by circumpolar deep water (~1.2oC). Interactions of ice shelves with such diverse oceanic environments result in drastic differences in ice shelves’ states. Their mass balance is controlled by different processes — ice advection and deformation in the case of cold oceans versus ice advection and melting in warm oceans. Their thermal structure is different — warmer interior in cold oceans versus colder interior in the warm oceans. They also respond differently to different mechanisms that lead to the increase of the ocean heat content (higher sensitivity to warming of the cold bottom water versus higher sensitivity shallower depth of the thermocline in the warm ocean).
A counter-intuitive difference in the thermal states of ice shelves floating in cold and warm environments is due to the fact that when an ice shelf flows into warm ocean, warm ice that resides near the bed of an ice sheet is eroded by strong melting and colder ice fills the interior of the ice shelf. In contrast, when the ice shelf flows into cold ocean, melting at its base is much weaker. Therefore it is thicker and warmer, because the warm ice near the bottom is not melted away. It is known that fractures form more easily in colder ice than in warmer ice. As a result, thinner ice shelves with colder interior have a greater chance to break up than warmer and thicker ice shelves.
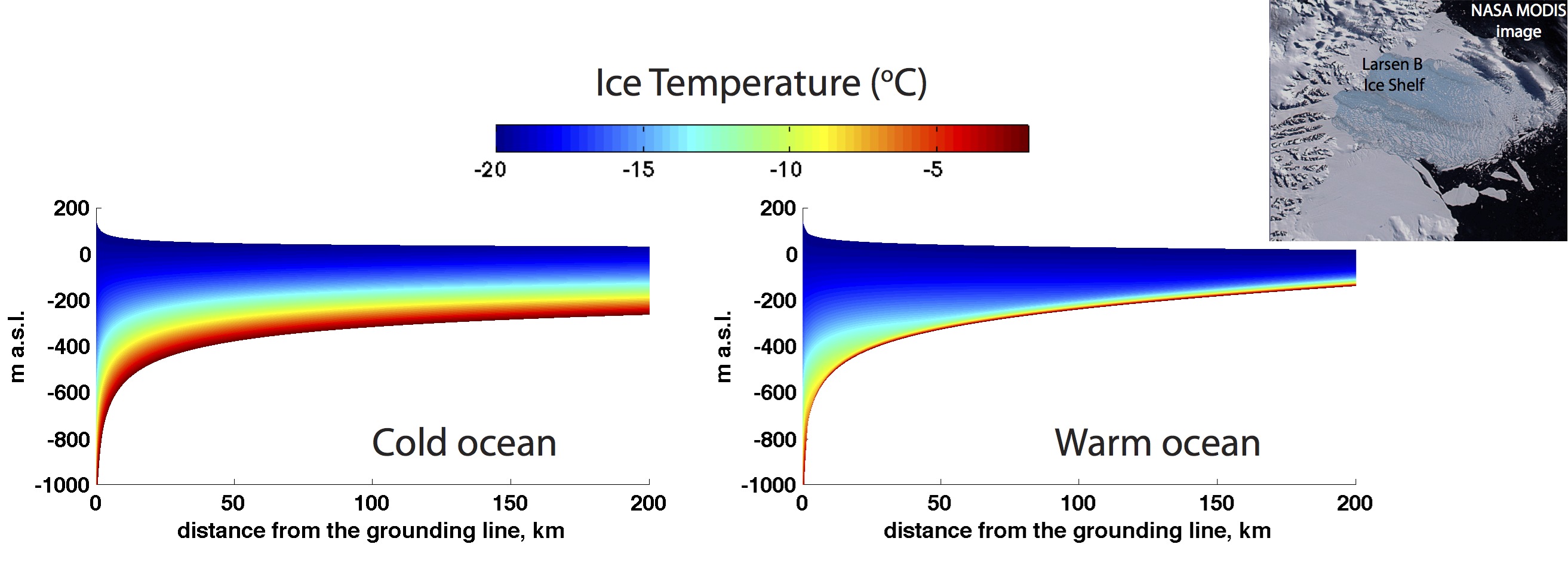
Figure 3 Internal temperature of ice shelves floating in cold and warm oceans. Inset shows MODIS image of Larsen B Ice Shelf.
Formation of melt-channels on ice shelves
Recent surveys of floating ice shelves associated with Pine Island Glacier (Antarctica) and Petermann Glacier (Greenland) indicate that there are channels incised upward into their bottoms that may serve as the conduits of meltwater outflow from the sub-ice-shelf cavity. Numerical simulations of a fully coupled ice-shelf/sub-ice-shelf cavity model show that these channels are a product of dynamical coupling of the ice-shelf flow and the sub-shelf ocean circulation. The morphology of the ice-shelf base determines how fast the buoyant plume adjacent to the ice-shelf base flows: the steeper the slope, the faster the plume flows. As the plume velocity increases, its ability to turbulently entrain underlying warm seawater increases, and thus the basal melting rate increases. This increased entrainment of warm underlying water increases melting and gives rise to even greater plume buoyancy, hence initiates a positive feedback between steep slopes, fast plume flow and enhanced melt rates.
Figure 4 Melt channels on the base of an ice shelf. Shape shows the shape of the ice-shelf base, colors show the plume flux. View from the grounding line towards ice front.
In the presence of the preexisting undulations topography upstream of the grounding line, plume flow accelerates in the locations where local basal slopes are steep, hence causes locally enhanced melting that makes preexisting undulations even deeper. The deepened channels are advected downstream with the ice-shelf flow. However, in these circumstances, melt channels do not preserve the shape and amplitudes of these topographic features. In circumstances where shear at ice-shelf lateral boundaries is non-negligible, its flow, hence flux, and as a result ice thickness are transversely nonuniform. The greater the lateral shear at the sides, the larger the difference between the horizontal velocity at the centerline and at the edge. As the magnitude of lateral shear increases, the basal draft difference also becomes larger between the centerline of the ice shelf and the edge. The transversely non-uniform ice-draft results in a speedup of plume flow where basal slopes are high. This means that there is the possibility of enabling a positive feedback between steep slopes, plume speed, and melt rates.
As a result, melt channels can form spontaneously where there is only a lateral ice thickness gradient generated by lateral shear in the ice-shelf velocity profile. In circumstances where the ice shelf has no-slip conditions at its lateral boundaries, the ice-shelf/sub-ice-shelf cavity system settles into a cyclic state, where spatial patterns of melt channels repeat themselves with a regular periodicity. The temporal evolution of these melt channels is driven by internal dynamics of the ice-shelf/sub-ice-shelf cavity system. This temporal variability happens in the absence of variations in external forcing, and so represent an internal mode of an ice-shelf/ ocean system. Dynamic interaction of the ice-shelf and the sub-ice-shelf circulation results in a highly variable spatial distribution of melting that manifests itself as self-organized melt channels.