Posted on June 26th, 2014 in Isaac Held's Blog
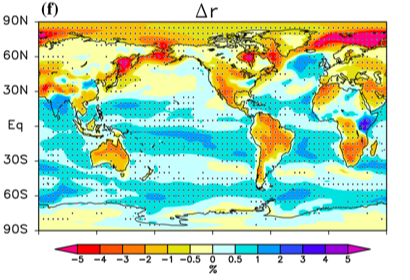
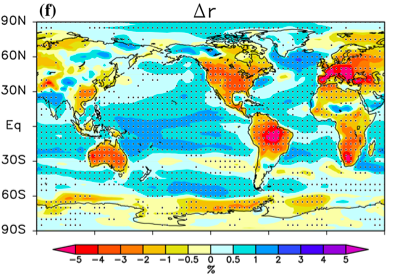
The change in near surface relative humidity averaged over CMIP5 models over the 21st century in the RCP4.5 scenario. Dec-Jan-Feb is on the left and June-July-Aug on the right. From Laine et al, 2014.
We expect the amount of water vapor in the atmosphere to increase as the atmosphere warms. The physical constraints that lead us to expect this are particularly strong in the atmospheric boundary layer over the oceans. The relative humidity (RH — the ratio of the actual vapor pressure to the saturation value) at the standard height of 2 meters is roughly 0.80 over the oceans. At typical temperatures near the surface, the fractional increase in the saturation vapor pressure per degree C warming is about 7%. So RH would decrease by about the same fraction, amounting to roughly 0.06 per degree C of warming if the water vapor near the surface did not increase at all. Why isn’t it possible for RH to decrease by this seemingly modest amount?
The figure shows what CMIP5 models predict will happen to RH near the surface by the end of the present century in the RCP4.5 scenario. In this scenario, which requires major mitigation efforts by mid-century, these models warm the tropics by about 1.6C on average, so fixed vapor concentrations would result in a decrease in RH of about 0.10. (I am avoiding expressing RH as a percentage to avoid having to talk about percentages of percentages.) The figure, from Laine et al 2014, shows RH over the oceans increasing by a modest amount, something like 0.01. (Over most land surfaces, RH is predicted to decrease — this is important, but I am going to focus on the oceans here since this is where most evaporation occurs.) So, to first order we can say that RH over the oceans does not change much in these simulations, relative to the decrease that would occur at fixed vapor concentrations. To second order RH near the surface over the oceans actually increases modestly.
To understand the first order picture, we need two pieces of information, one regarding the global energy balance of the troposphere and other regarding how the strength of the global hydrological cycle is related to near-surface RH.
The tropospheric energy balance to first order is a balance between radiative cooling and the release of latent heat when water vapor condenses. In the global mean there is roughly 80 W/m2 of latent heating. The change in this number in global climate models is typically only 1 or maybe 1.5 W/m2 increase per degree C warming in 1%/yr transient CO2 simulations (Pendergrass and Hartmann 2014), or at most 2% per degree C warming. Pendergrass and Hartmann provide a nice deconstruction of this number. Prevedi 2010 is very useful as well. There is a lot of literature on this energetic constraint on the strength of the hydrological cycle, starting, I think, with Betts and Ridgeway 1988. Aerosols — especially absorbing aerosols — can change things quantitatively quite a bit. But for our first order picture we only need to know not to expect large fractional changes in global mean evaporation or precipitation given the modest fractional changes in atmospheric radiative cooling involved.
The second point to appreciate is that the evaporation is controlled by the degree of sub-saturation of the air near the surface — roughly speaking by (1-RH) rather than RH itself. The air in contact with the ocean surface is saturated and it is the gradient in the concentration of water vapor between this surface air and the air near the surface that drives evaporation. If the relative humidity at the reference level is 0.80, the sub-saturation, 1-RH, is 0.20 and a reduction in relative humidity from 0.8 to 0.7 (as would be consistent with fixed vapor concentration in the warming simulation pictured above) would result in a 50%(!) increase in (1-RH). A 50% increase in evaporation is obviously ruled out by energy balance requirements. So we expect small changes in RH near the surface as the climate warms.
More precisely, evaporation over the oceans can be approximated by the “bulk formula”
Here and
are the saturation humidities at the ocean surface and reference level temperatures respectively,
and
are the relative humidity and wind speed at this reference level,
the atmospheric density and
a non-dimensional constant. A lot of physics and a lot of empirical evidence has been stuffed into the constant
, guided by what is affectionately known as Monin-Obukhov similarity theory. (All global climate models compute surface fluxes using Monin-Obukhov scaling as the starting point.)
depends on the height of the reference level, some properties of the surface (specifically surface “roughnesses”), and the gravitational stability of the atmosphere near the surface, which in turn is strongly coupled to the air-sea temperature difference.
If we ignore the air sea temperature difference as well as changes in wind speed and
, then we just have
. If the specific humidity does not change, then the large fractional reduction in
results in a huge increase in evaporation, as discussed above. But it even worse than that, because
will also increase by about 7%/C on top of the effect of the change in
.
Can the other factors in the expression for evaporation compensate somehow? The changes in tropical weather would have to be profound to produce reductions in average wind speed large enough to compensate for a such a large increase in . Fortunately, no models even hint at such profound changes. We can rewrite the expression for the evaporation as
For the term proportional to to compensate for the large reduction in RH this air-sea temperature difference would have to change sign, since the temperature difference is small — only +1 to +2C over the tropical oceans. But this temperature difference is itself constrained by an energy balance argument, as discussed by Betts and Ridgeway. [Due to mixing of water vapor in the turbulent boundary layer, the specific humidity is relatively homogeneous with height in this layer while temperatures decrease with height, so we often reach a point at which saturation occurs within the boundary layer, the cloud base. Latent heat release comes into play only above this level; something has to balance the radiative cooling below cloud base and it is the sensible heat transfer from the surface, proportional to the air-sea temperature difference, which has to pick up the slack.] And it is also extremely implausible that the value of C could cause this magnitude of an adjustment in evaporation (the easiest way of changing C is to change the air-sea temperature difference a lot). Something very dramatic would have to happen in the tropical atmosphere to avoid the constraint that near surface water vapor over the ocean must increase as the surface warms to maintain nearly constant relative humidity.
As for the second order picture, the small increase in RH over the oceans, note that the term would result in an increase in evaporation of 7% per degree C warming even if the relative humidity were fixed, and that this increase is already too large to be consistent with the energy constraint. An increase in RH of about 0.01, that is, a decrease in 1-RH of about 5%, is about the right order of magnitude to restore consistency. This seems to be part of what is going on in the CMIP5 composite at the top of the post. But now the changes are small enough that reduction in average wind speed and modest change in air-sea temperature difference could also play a role, as they seem to do in models. However, the models do seem to take advantage of the simplest way of throttling back the evaporation — a small increase in RH.
This near surface relative humidity is not just relevant for the lowest few meters of the atmosphere, since these near surface values are coherent with the humidity of the entire planetary boundary layer — the lowest 1-2 kms of the troposphere — because of the strong turbulent mixing throughout this layer. While the boundary layer is not where most water vapor feedback originates, it does contain a large fraction of the mass of water vapor. The increase in total mass of water vapor with warming has lots of consequences — for example, for the increase in the amplitude of the pattern of evaporation minus precipitation discussed in Posts #13 and #14.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Issac,
Thanks for the interesting post.
I tend to think the role of RH in damping the increase of evaporation with warming might be overestimated here based on my diagnostics of CMIP3 models ( Lu and Cai (2009) ).
In the post, you said ” An increase in RH of about 0.01, that is, a decrease in 1-RH of about 5%, is about the right order of magnitude to restore consistency.” but the 0.01 increase in RH (Laine et al. 2014) was not scaled with tropical warming, so the 5% decrease in [ d(1-RH)/(1-RH) ] would be only about 2~2.5%/K and therefore only explain part of slower increase in evaporation than C-C rate (about 6.5%/K) if the tropical warming is 2~2.5 Kelvin.
On the other hand, if the (1-RH) term did dominate in slower evaporation increase, then the decease in Bowen ratio over tropical ocean should be largely different from C-C rate because the decrease of sensible heat flux is not associated with RH (see Eq. 5 of Lu and Cai 2009), but the model results show that the change in Bowen ratio over tropical ocean basically follows C-C relation in CMIP3 models.
Jianhua,
You are right that I neglected to convert the small RH increase to an (even smaller) increase per degree C warming, so probably overemphasized the importance of the increase in RH for throttling down the evaporation below the C-C rate. The decrease in the difference between SST and air temperature that you emphasize is also seen in the CMIP5 results. Is there a simple way of getting at the relative importance of these two mechanisms? I probably need to read your earlier paper more carefully. (In any case, I should emphasize that this issue is related to the second order question of why we might expect a small increase in RH over the oceans with warming. The extreme unlikelihood of the system maintaining a constant specific humidity in the boundary layer over the ocean with warming is unrelated to this discussion.)
Isaac,
Yes, I agree that the at first order the system cannot maintain a constant specific humidity in the boundary layer over the ocean with warming through decreasing RH, and the specific humidity increases with temperature nearly by following C-C rate (as shown in Fig.1 of Held and Soden, 2006) .
We did in the 2009 paper try to decompose the relative importance of air-sea temperature difference, turbulent-transfer-coefficient (mainly the term C in your post, because the change in wind-peed is quite small) through near-surface stability, and relative humidity RH. We did so by introducing the fractional change of sensible heat flux. By substituting typical values of RH, Bowen ratio into Eq. 5b in Lu and Cai 2009, I tend to think the contribution of fractional change in air-sea temperature difference to the fractional change of latent heat flux be negligible ( because ( r*Bo*L*q/Cp) *dq/(qdT) << 1), but it could be important to the fractional change of sensible heat flux (SH).
If the contribution of RH change to fractional change of – Bowen ratio (also latent heat) is about 1-2 %/K, then Eq. 5b of Lu and Cai 2009 could tell us that the air-sea temperature difference may contribute 2-3%/K in fraction decrease of SH. Because the total fractional decrease of SH over ocean is about -5.2 %/K (Fig. 1b), then another about 2.2-3 %/K in fractional decrease of SH should come from the fraction change in C (labelled as beta in our paper which also included wind-speed). The change in C should contribute similar fractional decrease (2.2-3 %/K) to latent heat flux.
Then the total decrease in latent heat due to the change in C and RH would be about 4-5 %/K, and the net increase rate in latent heat (and hydrological cycle) is about 2 %/K.
Another evidence for the possible role of the change in C is in single-column models (SCM). I checked the single-column model in Lindzen, Hou and Farrell (1982) which was mentioned in Held and Soden (2006). By fixed turbulent transfer coefficient (C*V=constant, V the wind-speed) being prescribed in the SCM, the fractional increase in latent heat and precipitation in that model basically follows C-C rate. I found similar result (hydrological cycle change follows C-C rate) in an idealized SCM with fixed turbulent transfer coefficient but allowing changes in air-sea temperature difference. In this sense, we argued in the paper the energy constraint, which was used to explain the muted hydrological cycle to global warming, is not a priori, but a constraint from the internal consistency between thermodynamics (radiation) and dynamics (boundary layer dynamics, and tropospheric convective mass transport).
Jianhua, thanks for the detailed reply.
The issue you raise is whether the fact that the rate of increase in the strength of the hydrological cycle is much smaller in models than the rate of increase in water vapor, which increases at the C-C rate, can be understood just from thinking about radiative cooling of the troposphere or if other things related to the surface fluxes or boundary layer need to be taken into account. I can’t say that my own thinking has been that clear on this, but I like the Pendergrass and Hartmann paper linked to above, particularly Table 2 in that paper, which uses a radiative calculation, not in just one single column, but integrating over the globe. They focus on the clear sky, and get about 3W/m2/C for the response to temperature and water vapor, which is then reduced to 1.3 when the effects of CO2 (in these 1%/yr runs) are included as well. They also point out that the “total sky” change in radiative cooling of the troposphere is even smaller than this clear sky component. So this implies that radiative calculations are enough to make the case for the change in the hydrological cycle being smaller than the C-C rate.
Thanks, Isaac. I enjoyed the discussion very much, but hope my inputs would not go astray far away from the main point of the post.
I also like the Pendergrass and Hartmann paper and think their result robust and enough to explain the response of hydrological cycle to warming.
But there could be a possibility that the rate of hydrological cycle be following the C-C rate by different responses in profiles of water vapor, temperature, etc to 2CO2 forcing, but such a “manipulated” response will have to be at the price of breaking the well-established rule of turbulent mixing in boundary layer and near surface – for example, by fixing the C in model at a constant value. I am trying to do such an experiment with a GCM coupled with slab-ocean. I hope that the manipulated experiment would support the robustness of state-of-the-art GCMs, and also illustrate the atmospheric energy constraint are both thermodynamic and dynamic in its nature.
Hi Isaac,
Is there any quick explanation for the decreasing rh over land?
Does the sensitive heat and the moisture availability parameter (in a similar energy balance argument) make the difference here?
Thanks,
Wenyu,
I am going to try to get my thoughts together on that issue and return to it in a later post. In the meantime, you may want to read this.
Do observations of seasonal changes in relative humidity agree with the predictions of climate models?
i don’t have comparisons of model simulations of the seasonal cycle of relative humidity with near-surface observations handy. Perhaps a reader will be aware of a paper on this. Over land, comparing relative humidity patterns will likely reveal more or less the same biases that one sees when comparing seasonal cycles in precipitation. We routinely compare simulations with estimates of the spatial structure and seasonal cycle of column integrated water vapor, especially microwave data over the oceans. I hope to discuss aspects of that comparison here eventually.