NOAA GFDL - Geophysical Fluid Dynamics LaboratoryGFDL - Geophysical Fluid Dynamics Laboratory

Underestimated AMOC variability and implications for AMV and predictability in CMIP models

April 24th, 2018

Key Findings

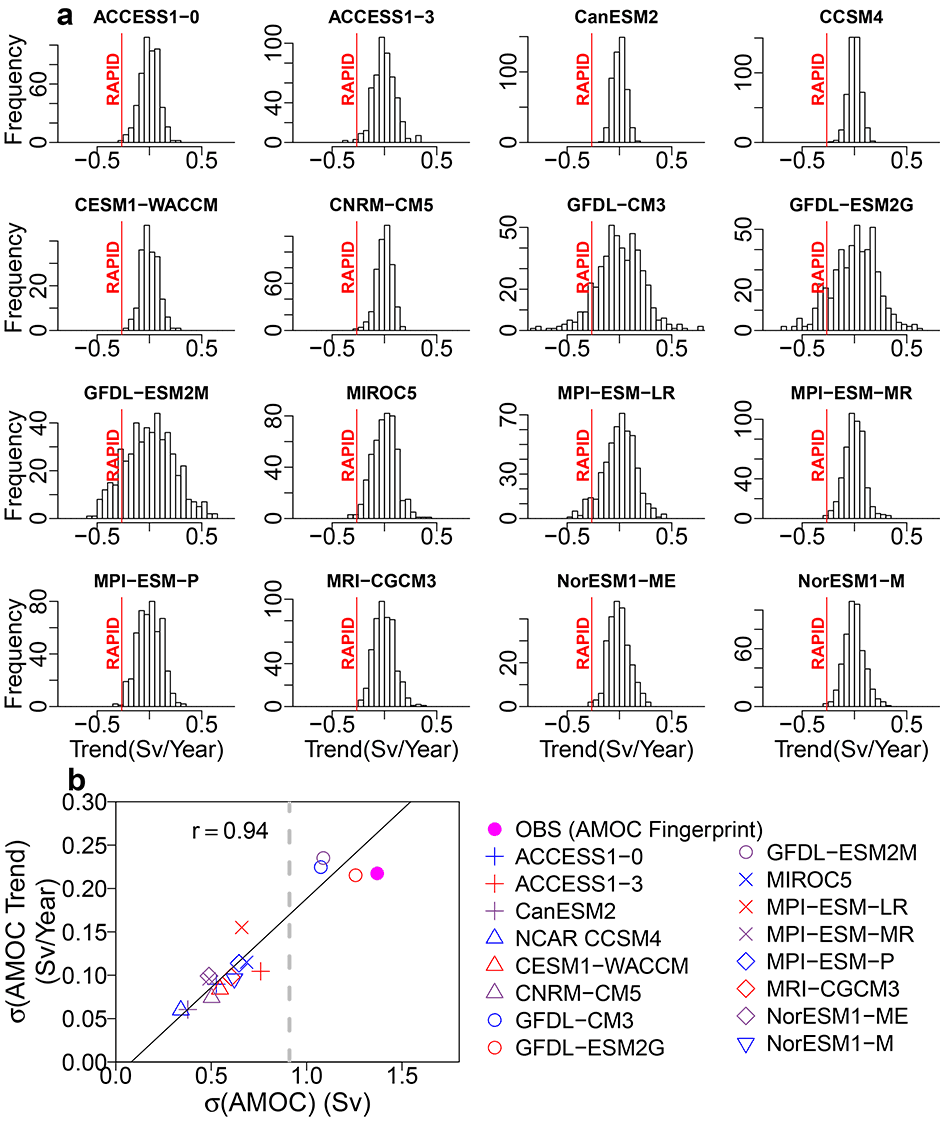
  • Most models underestimate the amplitude of low-frequency AMOC variability.
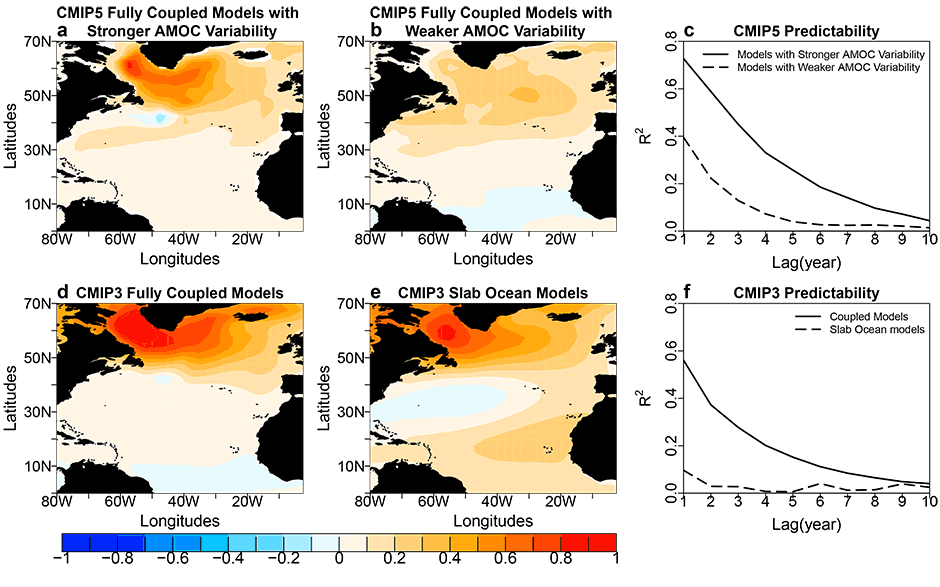
  • Given stronger low-frequency AMOC variability, linkages between the AMOC and the AMV and associated impacts on northern hemisphere surface temperature are stronger.
  • Atlantic decadal predictability is much higher (lower) in models with stronger (weaker) low-frequency AMOC variability.

Xiaoqin Yan, Rong Zhang, and Thomas R. Knutson. Geophysical Research Letters. DOI: 10.1029/2018GL077378

The Atlantic Meridional Overturning Circulation (AMOC) has profound impacts on various climate phenomena. Using both observations and simulations from multiple models of the Coupled Model Intercomparison Project, the authors estimated the amplitude of low-frequency AMOC variability in observations, compared it with those in model simulations, and examined the effects of low-frequency AMOC variability on the linkage between AMOC and Atlantic multidecadal variability (AMV).

This study provides a new perspective for understanding the important role of the AMOC in Atlantic multidecadal variability and associated impacts and predictability. These results indicate that the linkages between the Atlantic Meridional Overturning Circulation and Atlantic multidecadal variability, as well as the associated climate impacts and Atlantic decadal predictability, could be substantially hampered in models due to their underestimation of the amplitude of low-frequency AMOC variability.

Using both observations and simulations from the Coupled Model Intercomparison Project Phase 3 and 5 (CMIP3 and CMIP5), the authors show that most models underestimate the amplitude of low-frequency AMOC variability. In addition, stronger low-frequency AMOC variability leads to stronger linkages between the AMOC and key variables associated with the Atlantic multidecadal variability (AMV), and between the subpolar AMV signal and northern hemisphere surface air temperature (NHSAT). Low frequency extra-tropical NHSAT variability might increase with the amplitude of low-frequency AMOC variability. Atlantic decadal predictability is much higher in models with stronger low frequency AMOC variability, and much lower in models with weaker or without AMOC variability. These results suggest that simulating realistic low-frequency AMOC variability is very important, both for simulating realistic linkages between AMOC and AMV-related variables and for achieving substantially higher Atlantic decadal predictability.

The amplitude of low-frequency AMOC variability in observations has potentially important climate impacts. Identifying the limitations of models in simulating the low-frequency AMOC variability is helpful to understand and resolve the widespread linkages between the AMOC and the AMV, as well as the associated climate impacts in multiple models. Improvement of the simulation of the low-frequency AMOC variability may lead to enhanced Atlantic decadal predictability.

The 12-year AMOC trend distribution and its relationship with low-frequency AMOC variability. a), 12-year AMOC trends (Sv/Year) distribution from each CMIP5 control simulation, and the observed 12-year trend (red line) of the RAPID AMOC Index for the period 2004-2015. b), Scatterplot of the standard deviations of 12-year AMOC trends vs. the amplitudes of low-frequency AMOC variability in CMIP5 control simulations. Also included are estimates of the amplitude of low-frequency AMOC variability and the standard deviation of 12-year AMOC trends for observations (magenta dot), inferred from the reconstructed AMOC Index using the observed AMOC fingerprint. The grey dashed line separates the models into two groups with stronger and weaker low-frequency AMOC variability respectively, based on the amplitudes of low-frequency AMOC variability.
The most predictable patterns and their associated predictability in the North Atlantic. a,b) The most predictable pattern of SST in CMIP5 fully coupled models with (a) stronger or (b) weaker low-frequency AMOC variability. c) The predictability associated with the most predictable patterns shown in a and b. d,e) The most predictable pattern of surface temperature in CMIP3 (d) fully coupled or (e) slab-ocean models. f) The predictability associated with the most predictable patterns shown in d and e. Each pattern in (a,b,d,e) is normalized and has no unit, and the multiplication of the normalized pattern and its corresponding time series (which carries the unit) gives the temperature variations (in oC).