NOAA GFDL - Geophysical Fluid Dynamics LaboratoryGFDL - Geophysical Fluid Dynamics Laboratory

11. Is continental warming a slave to warming of the ocean surface?

Posted on May 24th, 2011 in Isaac Held's Blog

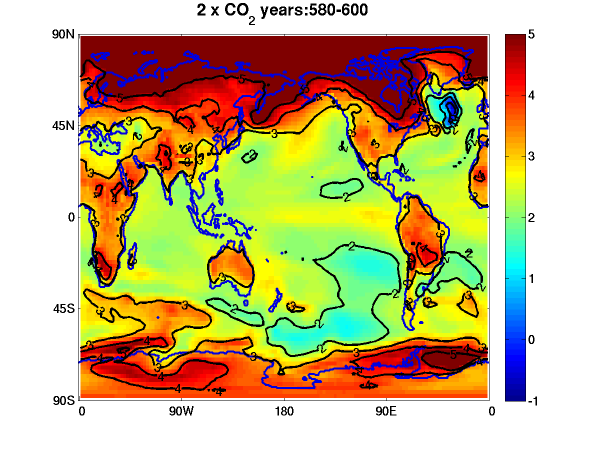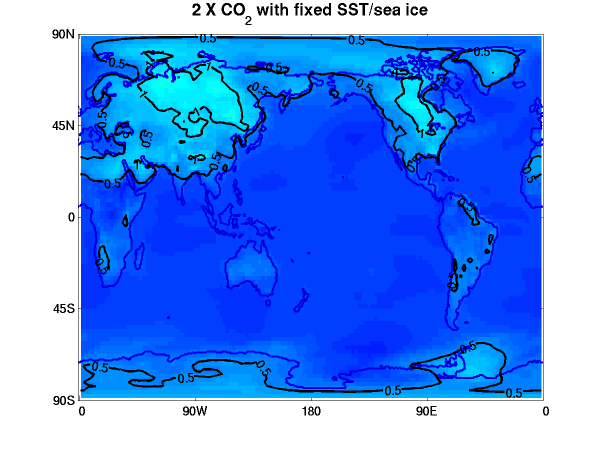
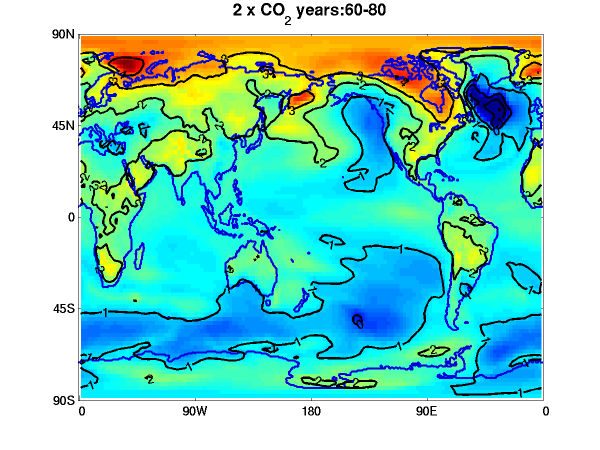
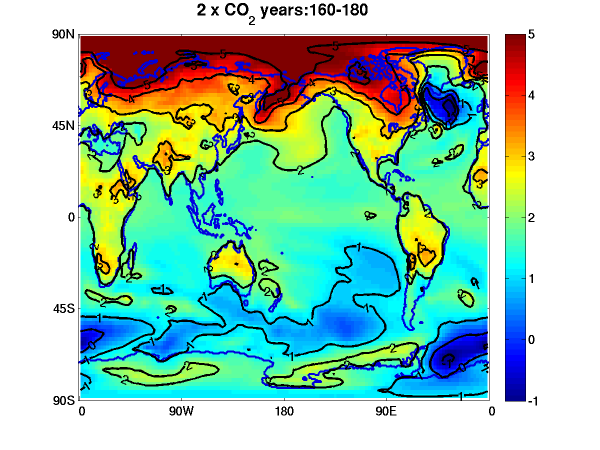
Annual mean surface air temperature response to a doubling of CO2.  Upper left: equilibrated atmosphere/land response (GFDL AM2.1/LM2.1) with fixed seasonally varying sea surface temperatures (SSTs) and sea ice. Other plots are coupled model (CM2.1) responses in a single realization with CO2 increasing at 1%/year till doubling (year 70) then held fixed.  Upper right — average over years 60-80, around the time of doubling; lower left — years 160-180; lower right — years 580-600.  Contour interval is 0.5C in upper left and 1C elsewhere.  Colors same in all plots.

 

Returning to our discussion of the time scales of the climatic response, it might be useful to take a closer look at the evolution of the warming in a GCM for the standard idealized scenario in which, starting from an equilibrated state, CO2 is increased at 1% per year until it doubles and is then held fixed.  This plot shows the results from our CM2.1 model.

I want to focus especially on the upper left panel; the other panels are mainly included here to provide context. The upper left panel is not generated from the fully coupled model, but from the atmosphere/land components of this model in isolation, holding the sea surface temperature (SST) and sea ice distribution fixed at their unperturbed climatological seasonal cycles, while doubling the CO2.   This model equilibrates to a change in CO2 in a couple of months (there is no interactive vegetation or even permafrost in this model, both of which would create the potential for longer time scales regionally).  The response depends on the season, so one has to integrate for at least a year before this annual mean pattern emerges.  We might call this the ultra-fast response, distinguishing it from fast (oceanic mixed layer), slow (oceanic interior), and ultra-slow (anything slower than the thermal adjustment time of the interior ocean, such as aspects of glacier dynamics).  One can visualize this as the first step in the response, but one that is evidently dramatically modified over time by the ocean warming and sea ice retreat.

(To think about this atmospheric relaxation time scale:  the heat capacity at constant pressure of air is 103 J/(Kg C), and multiplying by the mass of a tropospheric column of about 8 x 103 Kg/m2 gives a heat capacity for the column of 8 x 106 J/(m2 C); with a radiative restoring strength of 2 W/(m2 C)  we get a relaxation time of 4 x 106 s or roughly a month and a half).

This ultra-fast response is weak, far smaller than the transient climate response (defined as the global mean of the upper right panel).  Averaged over all of the continents, the surface air warming with fixed SSTs and sea ice is about 0.35C in this model, rising above 1C only in the interiors of the Eurasia and North America. So, in this model, most of the warming over land results from warming of the oceans (and, especially in high latitudes,  the retreat of sea ice). This qualitative result is robust across all of the models that I have ever  looked at.  A rough feeling for this coupling can be obtained from a simple diffusive model.  If one tries to mimic atmospheric horizontal energy transports in the midlatitude atmosphere with a turbulent diffusivity \mathcal{D}, the number one comes up with is about  1-2 x 106 m2/s.  To get something of this magnitude, setting \mathcal{D} \approx VL,  one needs, say,  V, an rms velocity, of 10m/s and L, an eddy mixing length, of  1-2 x 106 m.  (I have spent a significant part of my career trying to understand the characteristics of this tropospheric “macroturbulence”.) With a relaxation time scale \mathcal{T} as estimated above, the diffusivity penetrates a distance of about \sqrt \mathcal{DT} \approx 2-3 x 106 m. This is pretty crude and a little low, especially in the zonal direction, for which mean winds contribute to the transport .  (Jerry North and others have looked extensively at diffusive atmospheric models  in which the land-ocean geometry enters only through a spatially-varying heat capacity — for example, here).  So this GCM’s response with fixed SSTs is more or less as expected —  the atmosphere’s radiative relaxation time scale and the time it takes to mix from the oceans to the continental interiors are of comparable magnitude, so the warming over much of the land surface is tightly coupled to the oceanic warming.

Using a GCM, can we regenerate the land temperature record from the ocean record using observed SSTs and sea ice distribution as a boundary condition?  This is not simply a question of  “turbulent diffusion” by the atmosphere but also of  wave-like “teleconnections”  propagating away from regions of tropical convection that are altered by the pattern of tropical warming. Compo and Sardeshmukh, 2009 provide a recent discussion, strongly supporting the strength of  the oceanic constraint on land temperature trends.  So there does seem to be considerable redundancy between the observed land and ocean records of temperature trends.  This does not make the land record any less important.  Redundancy is critical when data sets and  models are imperfect.

One final point.  There is something else that one can do with the atmosphere/land only computation with fixed SSTs and sea ice: one can compute the globally averaged net energy flowing in at the top of the atmosphere (TOA), or, what is essentially equivalent, the energy flux into the ocean.  This is how we compute the “forcing” \mathcal{F}(t) for use in the simple energy balance model described in post #3.  There are things that happen on this ultra-fast time scale in response to the increase in CO2 other than the modest warming in the continental interiors, one of the most important being that the stratosphere cools.  If one tries to compute radiative forcing without taking into account the stratosphere cooling, one has to deal with a big difference between the energy imbalance between the TOA and the tropopause — this imbalance being precisely what causes the cooling.  But focusing on  the flux imbalance at the tropopause is a bit awkward, partly because the definition of the tropopause can be fuzzy.  It can be simpler to just let the model adjust the stratosphere as it sees fit, then see how much energy is flowing into the system.  This is an essential feature of the classical 1-D radiative convective model. In a GCM, fixing the SSTs and sea ice is a simple approximate way to do the same thing.  It seems to have the drawback that one is allowing the land to adjust a bit — and other things happen to the hydrological cycle as well — introducing some model-dependence into the definition of forcing.  But why allow some of the ultra-fast adjustment to occur (the stratospheric part) and not others?  Defining a “forcing” before the TOA, tropopause, and surface ocean fluxes come into agreement can be confusing  — for many purposes it is simpler to wait for the ultra-fast adjustment to occur to bring these three in line.

 

[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]

19 thoughts on “11. Is continental warming a slave to warming of the ocean surface?”

  1. This is a great blog, please continue to write it! Just to check that I understand this post, I’ll try to reformulate it.

    You split the model into several parts, according time scale. The first part is the ultrafast response. This is weak, but it’s output of it will drive everything that comes after it. A complication is that the ultrafast response depend on SST and ice cover, which changes over the next time scale. What you discuss in the first part of this post is this modulation. Given on the one hand a forcing (the CO2-level), and on the other hand a SST+sea ice cover level, we can produce a temperature map like figure 1, upper left.

    In the second part, which occurs at a larger time scale, convection is cleverly modelled as diffusion. Presumably, there is some differential equation formulation of this, so that given SST+ice cover and a temperature map (generated by the procedure in the previous step), we can compute the time derivative of SST and the sea ice cover. For this we would probably only need the part of that map the covers the oceans.

    After centuries, this leads to an equilibrium. From figure 1, it seems that the equilibrium response is almost an order of magnitude bigger than the ultrafast response.

    Two questions. I’m wondering how sensitive this procedure is to variations in the ultrafast response. If the eventual response (the equilibrium) is linear in the output of the fast response (this is not obvious), a small pertubation of the ultrafast response would be hugely amplified in the equilibrated state.

    I also assume that the model used incorporates responses up to the “slow”, but does not take the “ultra-slow” effects into account. Is that correct?

    1. You should not think of this ultra-fast response as driving the rest of the response. The latter should, I think, be thought of as driven by the radiative forcing left over after the ultra-fast adjustment. It would be of interest to compare the magnitude of ultra-fast responses in different models (for example, there are results described in the literature which suggests that ultra-fast cloud responses differ among GCMs), but I would not expect the magnitude of the TCR or equilibrium response to be correlated with the magnitude of the ultra-fast response across models.

      You are right that the model being examined here has no “ultra-slow” physics.

    2. Thanks! That was very enlightening to me. Nothing is more educational than making a stupid mistake, and having it pointed out.

      So the take home message is that the ultrafast response is not that important for the long term trend? I believe that this goes against a quite common (mis-)conception. But I do understand the logic in it. Part of the forcing will go to the ultrafast response, but the bigger part of the forcing will be used to increase the sea surface temperature and to some extent to melt sea ice. Those effects will not immediately show up on the thermometers, but they are crucially important for the long term temperature trend, and they should eventually control the land temperature.

      The way I’m thinking about this at the moment, we are trying to understand the long term behaviour of a complicated model (CM 2.1) by simpler approximations to it. This is essentially a mathematical problem. In the last sentence of the blog post, you suggest to “wait for the ultra-fast adjustment”. That sounds like a part of the approximation procedure. The ultra-fast response does somehow modify the forcing provided by the doubling of CO 2. Is there a way of quantifying that statement while staying in the world of the CM 2.1 model?

      1. Marcel, I think we are on the same page now. One can define “forcing” due to doubling of CO2 by doing the calculation in the upper left panel and just setting the forcing equal to the net energy input at the top of the atmosphere. This is not the only way to define “forcing”, but it is simple and convenient when trying to emulate GCM behavior with an energy balance model. Hansen et al (2005) compares this estimate of forcing with others in a particular model.

  2. Isaac: The experiment for the upper-left panel may under-estimate the role of land-surface warming in global-scale warming because it may suppress the water vapor feedback by fixing SST and the role of changes in horizontal energy and water vapor transport in the atmosphere. The about 1 degree warming in the interior part of the continents is close to the warming directly due to radiative forcing itself. But the warming smaller than 1 degree should be due to the changes (decrease) in horizontal energy (water vapor) transport between the atmosphere over land and that over the ocean. I guess there may be a negative water vapor feedback over those areas with warming of about 0.5 degree.

    I would suggest a different experiment that there are doulbing of CO2 over continents only, but the experiment allows the SST changes as in fully coupled GCM. I guess in this supposed experiment the fast land warming should be larger than that in upper left panel.

    1. The calculation that you suggest, allowing CO2 to increase only over land and letting the ocean and sea ice as well as the land respond, is very different from the one that leads to the upper left figure. My guess would be that it would result in about 1/3 of the response to all of the CO2, simply because you only have radiative forcing over 1/3 of the surface. The land/ocean warming ratio would be a bit larger than in the normal calculation, but not by that much because of efficient horizontal mixing.

      I don”t follow your interpretation of the fixed SST/sea ice calculation. The warming of less than 1K in most land areas is not due to negative water vapor feedback (I suspect that everything here can be understood to first approximation by holding relative humidity fixed) but just due to the strength of the mixing of air from the oceans, where the temperatures are pegged. The strength of the mixing wanes as one moves to the continental interiors, where the effects of the radiative perturbation are then felt a bit more strongly. My point is simply to note that the weakness of this response over land with SSTs/ice fixed implies that most of the warming over land in the freely evolving model is tied directly to the SST increase and sea ice withdrawal. The calculation that you suggest is interesting, but does not address the same question.

    2. Thanks. I also realized it should be about 1/3 of total 2XCO2 response after I posted the comment.

      I also agree that the mixing of the air from oceans important for the smaller warming, and ” that the weakness of this response over land with SSTs/ice fixed implies that most of the warming over land in the freely evolving model is tied directly to the SST increase and sea ice withdrawal”.

      My water vapor argument was mainly related to the water vapor supply from the oceans in the fixed SST/ice simulation which may be reduced due to the decrease in evaporation over oceans – In the the fixed SST/ice experiment the air temperature over oceans will still be increased due to the 2XCO2 forcing, then relative to fixed SST, the evaporation will decrease due to the decreased sea-air temperature difference. But this indirect effect may be smaller than the direct waning effect of the mixing.

  3. A bit off the main theme of this post…but I couldn’t help but notice the area in the North Atlantic of little or no warming under the 2X CO2 scenario. It seems to shrink somewhat over time but does not disappear even after 580-600 years. Is this due to a slowdown in the thermohaline circulation or something else…and is it seen in many other models too?

    1. Yes, this model has a substantial slow down in its northward heat flux by the Atlantic ocean circulation during a period of transient warming.

  4. Isaac: The central Figure of this post (top left) simply illustrates the critical importance of energy flux in the oceans. The top few meters (3?) of the oceans have the same heat capacity as the entire atmosphere. We have excellent data showing how the temperature of the oceans responds to seasonal changes in insolation. How well to models replicate the seasonal energy flux in the oceans and what does this suggest about their reliability over longer periods?

    1. Frank,

      It not just the heat capacity (which is effectively assumed to be infinite in the calculation that generates the upper left plot), but also the strength of the horizontal mixing within the atmosphere, that determines what the figure in the upper left looks like.

      The number is 2.4 m of water = heat capacity the atmosphere (at constant pressure).
      And, yes, many of the details of the seasonal cycle, including that of heat uptake by the oceans, are important tests for climate models.

  5. hello Isaac

    In 1910-1945, the SST increased by 0.41°C and the 1975-2010’s SST increased by 0.39°C.
    But in 1910-1945 the land temperatures increased by only 0.30°C while on 1975-2010 they increased by 0.73°C.
    How do you explain these increases different of land temperatures with the same SST increases?

    1. If all that is going on were the forced response to the well-mixed greenhouse gases, then I would expect these proportions to be pretty constant with time — climate evolution would then be self-similar. The extent to which it is not self-similar is our best evidence that more than one thing is going on, either internal fluctuations or other forced responses with different structures, in addition to the forced response to well-mixed greenhouse gases.

      1. thank you Isaac

        It is not entirely clear to me.
        If the land is the slave of the oceans, it is a slave regardless of the cause of warming.
        If the oceans are warming of 0.5 ° C due to climate variability (assuming that’s possible) or if they are warmed by 0.5 ° C following the CO2, the effect on land is the same or not?

        That is, the contrast LO is a signature of recent warming or not?

        That’s why I asked you the question for the period 1910-1945.

        1. A good question. A large part of the answer, I think, is the distribution of land and the distribution of the forcing with latitude. For example, there is relatively little communication between the two hemispheres on the 1-2 month atmospheric radiative relaxation time scale — it takes 1-2 years to begin to homogenize a tracer between the two hemispheres. So forcing concentrated in the Northern Hemisphere will naturally have more impact on land. To a lesser degree, this works within a hemisphere as well. This isn’t the whole story. Differing atmospheric dynamics at different latitudes come into play as well; the simple diffusive picture with uniform diffusivity is just a starting point for thinking about these things. Hope this helps.

  6. Rereading this post, I am confused about some of the aspects of heat transfer going on in the upper left panel simulation. I didn’t realize at first that the fixed SST condition implied any heat transfer into the ocean. I was imagining a reflective boundary of sorts I guess. I guess what in fact is going on is that the ocean is modeled as an infinite heat sink with an infinite thermal conductivity (all heat transferred to the ocean is just “lost” to the model). By contrast the land system (if included at all) would have a small heat capacity and a very low thermal conductivity, to make the scenario happen. By doing this, the atmosphere can act as it should; i.e. air parcels exchange heat with the surface as they move along it. Is this close to correct?

    1. Right, if you fix the temperature, as over the ocean here, you have to let the flux adjust to be consistent with that temperature — if you fix the flux (which is effectively zero over land) you have to let the temperature adjust to be consistent with that flux.

  7. Isaac, I wonder if you could take a look at a question I have about fixedSST simulations.

    Typically model aerosol forcing is diagnosed using this fixedSST setup. Wang et al. 2011 report split longwave and shortwave net TOA fluxes for one model and note:

    The longwave warming of 0.26Wm−2 is mainly from the contribution in the clear sky, which is caused in part by cooling over land surface (surface temperature over land decreases by 0.34 K) and therefore less thermal emission from land.

    This +0.26Wm-2 longwave flux compares to a total net flux of -1.05Wm-2. The global land temperature change quoted here is essentially the same as you report for a 2xCO2 perturbation. Is this surprising in the fixedSST setup given the ~3x greater forcing? I had a couple of thoughts: 1) As you talk about in the post, it’s difficult for land to warm very far without the ocean. Does this mean smaller forcings can typically cause about as much land warming as large forcings? 2) Surface forcing of aerosols is very large, which may substantially enhance surface temperature change in a fixedSST setup.

    Do either of these make sense as explanations?

    1. Presumably the fixed SST response over land per unit radiative forcing is quite a bit larger for aerosols than for CO2. (A related question is the extent to which it is possible to constrain the aerosol forcing with prescribed SST simulations.) I am always reluctant to presume that there is nonlinearity in this kind of model response until it is carefully demonstrated. I suspect that nonlinearity is not a dominant effect in fixed SST simulations.

Comments are closed.