Posted on September 15th, 2011 in Isaac Held's Blog
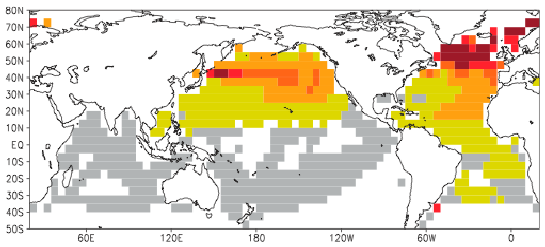 From DelSole et al, 2011 (pdf). The component of sea surface temperature variability that maximizes its integral time scale, obtained from the combination of 14 control runs of CMIP3 climate models.
From DelSole et al, 2011 (pdf). The component of sea surface temperature variability that maximizes its integral time scale, obtained from the combination of 14 control runs of CMIP3 climate models.
This is a continuation of the previous post in which I analyze the sources of my confidence that the warming trend of the past half-century is dominated by external forcing.
Taking a long control integration of CM2.1, a GCM that I have talked about here before, I’ve used the last 2,000 years from the simulation described by Wittenberg, 2009, and located the period with the largest positive 50-year trend in global mean surface air temperature. The picture below is of the trend at each point, the global average of which is 0.41C. The average over the Northern Hemisphere only is about twice as large.
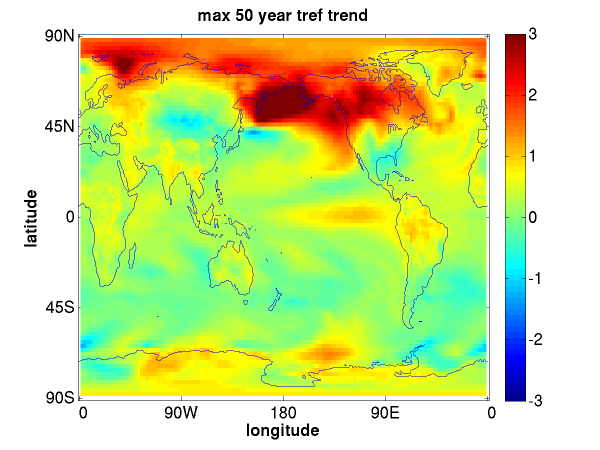 I think we can agree that this looks nothing like the observed trends in the past half-century. The maximum amplitude is in the subpolar North Pacific, with little trend in the tropics. Changes in the vertical mixing and transport between surface waters and deeper layers undoubtedly play a key role in the generation of this pattern. It is interesting that the North Atlantic does not play a more important role in this largest-trend case, since it does dominate the oceanic variability on somewhat shorter ~20 year time scales in this model. (The northern Pacific is too active, due to a cold bias and excessive ice formation, resulting in too much communication with deeper oceanic layers.) But there is one aspect of this pattern that does not surprise me — that the center of action is in the subpolar oceans.
I think we can agree that this looks nothing like the observed trends in the past half-century. The maximum amplitude is in the subpolar North Pacific, with little trend in the tropics. Changes in the vertical mixing and transport between surface waters and deeper layers undoubtedly play a key role in the generation of this pattern. It is interesting that the North Atlantic does not play a more important role in this largest-trend case, since it does dominate the oceanic variability on somewhat shorter ~20 year time scales in this model. (The northern Pacific is too active, due to a cold bias and excessive ice formation, resulting in too much communication with deeper oceanic layers.) But there is one aspect of this pattern that does not surprise me — that the center of action is in the subpolar oceans.
Here’s another plot, making the same qualitative point, from an older GFDL model– from Delworth and Knutson, 2000:
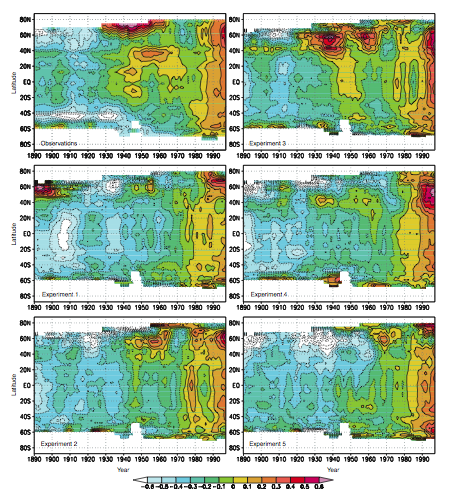
Shown as a function of latitude and time are averages over longitude of surface temperature from observations (here taken from Parker et al, 1994) in the upper left and from 5 realizations of the climate model’s simulation of the 20th century. The differences between realizations is the internal variability, and one can see quite a lot at high Northern latitudes in this model. In fact, one of the realizations (upper right) happens to capture considerable early century warming, peaking near mid-century in high northern latitudes, comparable to that observed. (This ability to capture early 20th century warming due to internal variability remains rare in models, with this result a bit of an outlier –whether this is due to underestimation of variability by models or the presence of other forcings remains the obvious question.) In any case, internal variability is unable to compete with the more uniformly distributed warming trend throughout the tropics and midlatitudes of both hemispheres in the latter half of the century.
DelSole et al 2011 provide a convenient figure (top of post) summarizing the spatial structure of low frequency variability of sea surface temperature in an ensemble of GCMs. They gather the control simulations from 14 models together into one pot and decompose the variability into patterns, isolating that pattern whose time series has the largest integral time scale (or decorrelation time). This is not the only way to summarize this information, but it serves my limited purpose here of illustrating how low frequency variability tends to be concentrated in the subpolar oceans across the model ensemble. (They exclude the Southern Oceans from their analysis.)
Water columns are much more strongly stratified in the tropics than in higher latitudes, so it takes a lot less energy to move parcels from deep oceanic layers to the surface in high latitudes — and, not surprisingly, this is where most communication occurs between deep and surface waters. On the other hand, it seems quite logical that one needs to tap into the heat capacity of these deeper layers to create internal variability on long time scales. So one can rationalize the result that the centers of action for internal variability in the oceans migrate poleward from the tropics and subtropics to higher latitudes as one moves to lower frequencies. By the same physical argument, one expects minima in the response to external forcing in the subpolar oceans, since these are being held back by their strong coupling to the deeper layers.
We can all question these model results, of course. For example, could unresolved mesoscale eddies create more energetic multi-decadal variations in the wind driven gyres by cascading energy to larger scales? Also, temperature anomalies like those in the figure at the top do influence tropical rainfall patterns. In fact, they may do so more efficiently than more uniform temperature change; warming one hemisphere with respect to the other is an excellent way of pulling monsoonal circulations and oceanic ITCZs towards the warm hemisphere (the last few years have seen numerous studies of this response, relevant for ice ages and aerosol forcing as well as the response to high latitude internal variability; Chiang and Bitz, 2005 is one of the first to discuss this, in the ice age context; I’ll try to return to this topic in a future post.) Could tropical cloud feedbacks, or the coupling to ENSO, amplify the effects of low latitude hydrological responses to high-latitude anomalies in these models?
In any case, it is good to have a list of what you have to question if , in particular, you want to argue that the warming in the past half-century has been dominated by internal variability. It is not enough to look at global or hemispheric means of surface temperature and note that the models are not that far from producing internal variability of the right magnitude — perhaps most existing models only do this once in a blue moon, but I can imagine increasing the variance at low frequencies by a factor of two, say, so that the required magnitude is achieved more frequently. But the spatial structure will be still be wrong. My intuition is that it will be harder to modify the structure than the amplitude of the variability.
If a model comes along with low frequency variability that is less polar concentrated and fits the century, or half-century, trend pattern better, that would be news. If it also has heat flowing into rather than out of the oceans during the growth of the warm phase of this mode, that would be even more dramatic news.
Can we analyze observations cleverly so as to separate forced from internal variations, with or without the use of models? If we had higher confidence in the evolution of the aerosol forcing over time it would be a lot easier. But there are a number of recent attempts, including the Delsole et al paper cited above, that we can discuss as we go along. In light of the plausible structure of internal variability (and the relatively rich set of observations of the North Atlantic ocean) a focus on high Northern latitudes, asking if some of the observed trend in this region is internal, might be more productive that a focus on global means.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Hello Isaac
“If it also has heat flowing into rather than out of the oceans during the growth of the warm phase of this mode,”
If the heat is flowing into rather than out of oceans, it is due to forcings, no?
And in this case it should be “internal forcings”.
But the notion of “internal forcings” means that what we consider only as temperature feedbacks, as the clouds or the water vapour, might be differentiated from temperature and might depend from others parameters.
It was, if I understood, one part of a recent discussion between Spencer and Dessler.
My comment was just a reference to my previous blog post on heat uptake trends when there is a superposition of forced and internal variations. I don’t see this as related to the Spencer/Dessler discussions, where the issue concerns time scales on which coupling to the deep ocean is irrelevant.
Isaac. I learned a lot from this post. In case you are interested, you can download the pattern that maximizes the integral time scale over global SST (including the Southern Ocean) here. As expected, the largest amplitudes occur in the subpolar regions.
A question that puzzles me is why this pattern is correlated between the Northern and Southern hemispheres, and between the Atlantic and Pacific basins. In separate calculations, I obtain similar results by optimizing the pattern in distinct basins individually and then estimating the pattern in other basins by regression, suggesting that the global, same-sign character of the pattern is not an artifact of the EOF truncation used in the analysis. Even your trend pattern suggests a global, same-sign structure. Is there a reason to believe that internal mechanisms will generate same-sign anomalies in both hemispheres on multidecadal time scales?
Tim, thanks for the global plot. As for the consistency in sign, my rule of thumb has been that there is no significant communication between the north and south polar regions through the atmosphere (this comes up in the context of glacial-interglacial fluctuations) so it would have to be oceanic. And my impression has been that AMO variability produces opposite signs in the two hemispheres as one would expect from a change in pole-to-pole overturning, albeit with the changes much larger in the north, so I am a little puzzled by your result. A response emanating from the tropics can create same sign responses in the two hemispheres, but I see little sign of that in your plot. I guess I would worry whether the model drift has been removed adequately.
The temperature of higher latitudes probably shows more natural variability because it takes a smaller variation in energy flux to change the temperature where it is colder. When considering global oceans, it would be interesting to see where variation in energy flux is greatest. (I presume this could be done by dW = 4oT3.dT and dT is your temperature variability.)
The issue is that variability shifts to higher latitudes as the frequency is lowered. The effects of differences in radiative restoring that you refer to may be significant, although even here I do not think that these differences are primarily due to the ; my impression is that high latitudes have weaker radiative restoring because surface temperature perturbations are not as strongly coupled to the troposphere so have more difficulty radiating to space.
; my impression is that high latitudes have weaker radiative restoring because surface temperature perturbations are not as strongly coupled to the troposphere so have more difficulty radiating to space.
Isaac,
“If it also has heat flowing into rather than out of the oceans during the growth of the warm phase of this mode, that would be even more dramatic news.”
I cannot help but think that this would require that most of the warming is in some way radiatively forced and only initiated and temporarily sustained by an internally induced rise in temperature.
Can this occur without the risk of runaway instability?
Well it would have to be immune to a temperature rise due to a uniform forcing, which could be satisfied if the induced forcing (radiative) was proportionate to a positive temperature difference between an initiating region (where the internal forcing would take place) and a responding region. If the responding region had the larger area this could still give rise to a net uptake of heat during most of the warming phase. A uniform forcing, if it failed to cause a temperature difference that reinforces the warming, would not be unstable and if uniform forcing drove the temperature difference the other way this would imply a negative feedback and enhanced stability.
Were this to be possible and actually occur, it would I think be apparent in the spatial pattern of boundary fluxes if not markedly so in the pattern of the heating. In the initiating region there would be a net flux from the internal source (presumably oceanic) into the atmosphere and out through TOA (local negative feedback) and the reverse of this in the larger responding region. If the responding region were much greater in area than the initiating region the response could be smaller in terms of flux per unit area than the absolute value of the opposite flux in the initiating region.
Is it something like this that would be required?
Alex
Alex, I think this is one way of doing it — the energy balance of the Earth would have to be controlled by a small region that in itself was not strongly affected by the energy balance. Actually, I think something like this does happen to a modest degree in El Nino, superposed on the natural radiative damping to space, but big enough to give you phase lags a la Spencer and Braswell.
Professor Held,
It seems to me that you are looking downwards here when you should perhaps be looking up. Figure 9.3 of AR4 WG1 suggests that there was a substantial increase in SHORTWAVE heating between start of satellite monitoring and 1998. The GCMs stayed flat over this period. The true difference between the models and observations is somewhat masked because Figure 9.3 recentres each plot to its own average value over the period. However, doing a crude eyeball integration, the energy difference amounts to something greater than 10 watt-years/m2. Nasa’s ISCCP confirms an increase in received SW flux over this critical period amounting to a change of 4W/m2. Several respectable papers, some mentioned in the same section of AR4 WG1 Chapter 9, have attributed this large fall in effective albedo to change in cloud cover. In parallel, we have seen evidence in Lindzen and Choi 2010 that LW emission in the models is low relative to observations – even if one doesn’t accept all of the conclusions from the paper – which would help balance the books in terms of energy balance. Since 1998 albedo has increased, also for unexplained reasons, and temperature has moved sideways. Surely, the more relevant attribution question is what caused these changes in albedo? Temperature feedback (which seems unlikely given the magnitude and profile in time) or something different?
This thread derives from the question you posed on the previous thread, which was based on a model which seems, with no disrespect intended, deeply flawed. I believe that it confuses temperature and time. Whatever the distribution of heat in the coupled system, we still expect the total energy gain for the coupled system to be determined by the difference in net flux. dH/dt = F- f(T) where F is the forcing, f(T) is the feedback term, T is temperature perturbation. Just because you add in another term which has temperature in it does not mean that the total energy gain changes. All you are actually doing is seeking to partition the energy differently, and using temperature as a discriminant. This may sound like a trivial distinction, but it’s not.
The climate sensitivity and the shape of the net flux vs temperature profile is FULLY DETERMINED by the basic energy balance equation above – no matter how you decide to partition the rate of energy gain. The net flux is F – f(T). You plot it against T. This is not dependent on how you partition dH/dt. Equally for climate sensitivity. As equilibrium is approached dH/dt -> 0. The equilibrium temperature for a fixed forcing F is then given by the smallest positive root of the expression F -f(T). Still no energy partitioning required to do this.
You however are assuming (it seems to me) that because when you plot net flux against T, you don’t get a straight line, that the explanation must be something to do with how fast or slow the ocean heat uptake is. No. F – f(T) is a net flux and it does not care where its radiant energy goes. If you don’t get a straight line when you plot F – f(T) against T it can only be because f(T) is non-linear.
The ocean heat uptake and the effective capacity of the system do however have a (potentially large) effect on the time it takes to reach theoretical equilibrium. I’m afraid I think that your assertion here is poorly founded.
I don’t actually disagree with much of what you say, so I may be missing something. I assume that you are referring to post #5 as regards the “nonlinearity” of your f(T). You can call this nonlinearity if you like, but as I tried to argue in that post, I think it is better to regard it a linear in the temperature field — it is just that this field changes its structure as a new equilibrium is reached. I won’t repeat that argument here, but it is not a given that the global mean flux is just a function of the global mean temperature — what if it is linear in both tropical and high latitude temperatures, but with different constants of proportionality? The ocean heat uptake comes into play only when one is trying to explain why the structure of the warming in models changes in time — that is, why the high latitude warming is delayed.
As for the interpretation of the TOA fluxes and temperatures over the past decade, this is a fascinating problem that I expect to come back to eventually in other posts. But in post #5 I was just trying to understand a GCMs behavior on multi-century time scales, which seems like a rather different problem to me. If you want to discuss this further, let’s do it under post #5 to keep things a bit organized. All posts are kept open for comments.
Thanks for the response, Professor Held. I don’t believe that your (valid) argument about distribution of temperature fields does more than throw a couple of shovelfuls of earth into the conceptual hole. But I am not sure that I can demonstrate that either in a comment here or in #5. I was planning on submitting a post to Lucia’s Blackboard explaining why the IPCC feedbacks were case-sensitive. Since the question of what controls the non-linearity in net flux vs temperature is central, I will instead substitute a post which sets out my views and invite you to comment either at Lucia’s or on your own blog. If I am wrong on this, I would prefer to know it.
The warming during the early/mid warming phase looks spatially similar to the present warming phase presumably with very different forcings (i acknowledge the paucity of data).
In climate models do all ‘external’ forcings give similar spatial patterns?
No, in particular the aerosol response has a very different structure in models than the well-mixed greenhouse gases, since the forcing is primarily in the Northern Hemisphere, a difference that forms the basis for most attempts in the detection/attribution literature to separate responses to aerosol from well-mixed greenhouse gases.