Posted on August 23rd, 2011 in Isaac Held's Blog
Suppose that most of the global mean surface warming in the past half century was due to internal variability rather than external forcing, contrary to one of the central conclusions in the IPCC/AR4/WG1 Summary for Policymakers. Let’s think about the implications for ocean heat uptake. Considering the past half century in this context is convenient because we have direct, albeit imprecise, estimates of ocean heat uptake over this period.
Set the temperature change in question, , equal to the sum of a forced part and an internal variability part:
, with
, so
is the fraction of the temperature change that is forced. The assumption is that this is a linear superposition of two independent pieces, so I’ll write the heat uptake as
.
When the surface of the Earth warms due to external forcing, we expect the Earth to take up heat. But what do we expect when the surface warms due to internal variability? Can we use observations of heat uptake to constrain ?
The strength of the radiative heat loss to space per unit warming of global mean surface temperature is a key quantity of interest, as usual. In post #5 I tried to emphasize that this parameter, which I denote by , should depend, among other things, on the horizontal structure of the surface warming. This issue is of vital importance when discussing observational constraints on climate sensitivity, since the natural changes we observe – due to ENSO, AMO, volcanoes – do not all share the same horizontal structure as the forced response to CO2.
But consider the two limiting cases: either the forced response dominates the half-century trend or internal variability is dominant. If both of these limiting cases are going to be viable, then they both have to have the same spatial structure, that of the observed warming. (In actuality, I am very skeptical that internal variability can create this spatial structure, but I am suspending this skepticism for the moment.) So, within the confines of this argument, with the intent of focusing on the limiting cases, it is interesting to assume that the strength of the radiative restoring is the same for the forced and the internal components.
For the forced response, I’ll use the framework for discussing the transient climate response in post #4 in which the forcing is balanced by the radiation to space and heat uptake, both of which are assumed to be proportional to
:
. So
, and the heat uptake
associated with the forced response is
. A fraction
of the radiative forcing is taken up by the Earth, the rest is radiated away due to the increase in temperature. This fraction can be quite modest. For example, using the numbers that mimic the behavior of GFDL’s CM2.1, a GCM discussed in post #4, this ratio is 0.7/(1.6+0.7)
0.3 . In this sense the forced response is rather inefficient at storing heat.
I am going to assume that and
are given and that the value of
is the point of contention. The fraction of the response that is forced depends on the value of the radiative restoring
according to
or, expressing as a function of
,
.
Meanwhile suppose there exists internal variability with the spatial structure of the warming trend. As discussed above, I assume that it radiates energy to space at about the same rate as the forced response of the same magnitude. So the contribution of this internal component to the heat uptake is , and the total heat uptake is
Substituting for , the heat uptake as a function of
is
or, in a non-dimensional form,
The first term is the uptake per unit forcing computed as if the entire temperature change were forced – the second term is the correction needed if internal variability contributes. It is important that this second term is more or less inversely proportional to ; a bigger
(smaller climate sensitivity) is required to make room for the internal contribution, resulting in stronger radiative restoring of this internal component and greater heat loss.
A typical value for the first term, , might be
0.3 as already discussed above. Using this estimate, the value of
needed to produce near zero heat uptake by the oceans is
, so internal variability need only contribute about 25% of the total warming to fully compensate for the heat uptake due to the forced response. If internal variability contributes 50% of the warming, then the heat lost by the oceans would be more than twice as larger as the heat gain computed by the alternative model in which the internal variability contribution is small. This heat loss increases more and more rapidly as
is reduced further.
While the specifics of the calculations of heat uptake over the past half century continue to be refined, the sign of the heat uptake, averaged over this period, seems secure – I am not aware of any published estimates that show the oceanic heat content decreasing, on average, over these 50 years. Accepting that the the sign of the heat uptake is positive, one could eliminate the possibility of — if one could justify using the same strength radiative restoring for the forced and internal components.
But this little derivation cannot be taken at face value when is large. If one accepts that the forced response dominates, one can consistently free up the horizontal structure of the internal component, potentially producing a dramatically different, and possibly much weaker, radiative restoring for the internal component– and allowing
to be reduced more than indicated by this calculation before the heat uptake changes sign.
I have recently looked at 1,000 years of a control run of CM2.1 (with no time-varying forcing agents) and located the 50 year period with the largest global mean warming trend at the surface, which turns out to be roughly 0.5K/50 years. This warming is strongly centered on the subpolar Northern oceans, diffusing over the continents, but with little resemblance to the observed long-term warming pattern. (We don’t have a lot of confidence in the model’s simulation of these low frequency variations, but you can argue on very general grounds that these low frequency structures should emanate from the subpolar oceans. I’ll try to return to this issue of the spatial structure of low frequency internal variability in another post.) Heat is being lost from the oceans to space in this period, but at a much slower rate than in the forced response to CO2, due in large part to positive feedback from polar ice and snow (and low clouds over the oceans) in the model. As discussed in post #5, it seems that the more polar concentrated the response the weaker the radiative restoring.
I am not aware of any study summarizing the strength of the global mean radiative restoring of low frequency variations in control simulations in the CMIP3/AR4 archive. It would be interesting to look at these if someone has not already done so. Supposing that we accept the model results for this radiative restoring of low frequency internal variability,what does this yield for the value of at which the heat uptake changes sign?
Like many others, I am watching with great interest and, I hope, an open mind, as the heat storage estimates from ARGO and the constraints imposed on steric sea level rise by the combination of altimeter and gravity measurements slowly emerge. And I would like to understand the effects of internal variability on heat uptake a lot better. But I see no plausible way of arguing for a small- picture. With a dominant internal component having the structure of the observed warming, and with radiative restoring strong enough to keep the forced component small, how can one keep the very strong radiative restoring from producing heat loss from the oceans totally inconsistent with any measures of changes in oceanic heat content?
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



As I understand there is still no guarantee that the recent increase in global temperature is not the result of natural internal variability?
There is also something I wonder.
Natural variability could it not occur by a change in the overall sensitivity?
As far as there being a “guarantee”, all I can say is that I personally have no idea on how to create a consistent model dominated by internal variability — ie., a model with low climate sensitivity, a trend pattern similar to observations, and a positive heat uptake — as I tried to outline in this post.
With respect to creating internal variability through alterations in the strength of the radiative restoring, if this restoring strength depends on the state of the system in different ways, I can see it enhancing pre-existing variability, conceivably. It is harder to visualize it creating variability from scratch. But there are all sorts of possibilities. If you have some simple equations that capture what you are thinking about then it would be easier for me to comment.
hello
I hope you will forgive my bad english
I don’t know what mechanism may cause the climate sensitivity is variable.
But assuming there is an unknown oscillating oceanic mechanism, for example, which varies ,in important parts of the globe, the low clouds, there can be variation in the albedo, regardless of global temperature.
Low clouds are certainly feedback but locally, at home, for example, for the same surface temperature sometimes I have clouds and sometimes I have no clouds. (sorry I am trivial)
So of course we can all imagine and that’s why we have models.
The admission of people like Hansen, however, the models are far from perfect and may not know some important mechanisms.
Otherwise, I did a little experiment, taking a sensitivity of 1.2 K.m2 / W with sine wave superimposed 100-year period and amplitude 0.1K.m2 / W.
I start with a forcing constant 242W/m2 (I know the sensitivity of 0 to 290K can not be constant but to simplify it) and I get the graph below.
http://a403.idata.over-blog.com/1/39/27/52/images9/aout-2011/held-reponse.jpg
I get the equilibrium temperature after about 4000 years (on a multi-layer ocean) and cyclical variations in temperature are 6K/50 years with a fairly low variation of the overall sensitivity.
As I understand it your model is (simplifying your ocean down to one layer for simplicity):
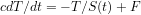 where
where  is a constant and
is a constant and 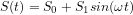 — and
— and 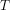 is the absolute temperature. I’ll describe the system as one with the equilibrium state generated by setting
is the absolute temperature. I’ll describe the system as one with the equilibrium state generated by setting  with the perturbation produced by turning on
with the perturbation produced by turning on  . The temperature in equilibrium is
. The temperature in equilibrium is  . Assuming that
. Assuming that  , the perturbation
, the perturbation  satisfies
satisfies  . I would refer to the second term as the "forcing" — the energy input to the system assuming that temperatures are unperturbed. This has amplitude
. I would refer to the second term as the "forcing" — the energy input to the system assuming that temperatures are unperturbed. This has amplitude 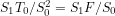 , which is 24
, which is 24 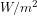 ! So you have huge "forcing", in the language that we use, and naturally you get very large temperature responses from what seems to be a small fractional change in "sensitivity". The temperature response then depends on your effective heat capacity.
! So you have huge "forcing", in the language that we use, and naturally you get very large temperature responses from what seems to be a small fractional change in "sensitivity". The temperature response then depends on your effective heat capacity.
Dear Prof. Held,
I’d just like to make sure I understood your post correctly:
the common answer to the “contrarian talking point” that much of the observed recent climate change could just be caused by natural variability in the climate system is that this would imply, broadly speaking, heat being moved from the oceans to the atmosphere – whereas we observe the opposite, oceans storing heat. Your post here refines this answer with theoretical calculations sowing that – even with optimistic considerations on the radiative and spatial properties of a”natural” surface temperature change – the fraction of temperature change resulting from natural variability can not exceed ~25% in order to remain consistent with the observed positive sign of ocean heat content change (only the sign, no even the absolute value). Is that right ?
This seems to depend partly on the 0.3 model fraction (heat uptake to radiative forcing in a forced response) you’re mentioning. How confident would you be on that value ? for instance if it was 0.5, “Xi” could fall to 66% (and I note that in any case in this framework Xi can’t go below 50%… ?)
thank you.
Basically, you have it right. You can substitute your own numbers; if the forcing is more efficient at putting heat into the system per unit warming then you can have a larger internal component before you flip the sign of the heat uptake.
But the main issue with this estimate is the assumption that the strength of the radiative restoring is the same for internal and forced responses — which I interpret as assuming that the spatial structures of the warmings are similar, and there is no reason to assume that this is the case in general.
Isaac,
I will confess that I was initially baffled by this post, for it was my prejudice that the general increase in OHC over the last ~50 years leaves so little room for benign warming due to some internal variability, that is I failed initially to see what case had to be answered and hence I failed to comprehend your argument. Thankfully I have it now.
As I understand it, attempts to propose a “purely” internal mechanism and simultaneously balance the energy book must either embrace or ignore an implication, during a period of rising OHC, that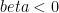 on average. Which would not be benign.
on average. Which would not be benign.
Attempts to show a large or dominant share for some internal mechanism would similarly imply that ~ 0. Again hardly benign.
~ 0. Again hardly benign.
This is commonly answered by a "you can't have it both ways" argument, that you cannot have a dominant internal mechanism and low sensitivity.
One fairly popular conjectured internal mechanism is some sort of ENSO pump. That during the current era, ENSO has been pumping up the temperature. I presume this be due to a non-linearity in the global response to positive and negative ENSO phases but I have not heard it expressed in those terms.
As I see it there would be the implication that during the positive phase the climate is on average unstable with rising temperatures resulting in net heating globally but during the negative phase the climate is stable. Thus the warming is due to an era of strong or some anomalous type of ENSO fluctuations.
This is not something that I believe. I will repeat that the non-linear mechanism is something I have inferred from energy balance considerations, i.e. it is not necessarily part of the conjecture as it is stated.
If anyone will allow my having extremely high sensitivities or an era of temporary climatic instability I could dream up other candidate mechanisms, e.g. integrated TOA flux noise but they all face the same problem regarding what to do about GHG forcings in a world with an extreme climate sensitivity.
I should also like to think I have an open mind, and I do expect refinements and perhaps even some surprises as the OHC estimates are revised, but not so open that I can expect the trend to be reversed.
Regarding your closing question:
"… how can one keep the very strong radiative restoring from producing heat loss from the oceans totally inconsistent with any measures of changes in oceanic heat content?"
How, indeed! Beats me!
FWIW it is my prejudice that the AR4 claim "very likely" "most of the warming" etc. is sufficiently weak to be safe against arguments that do not rely on very high sensitivities e.g. a random walk, with the possible exceptions of some unappreciated dominant forcing or that old standby that "the climate is chaotic to a degree that permits all possible outcomes".
Now that I have understood your post, I must add that I do think it is very worthwhile going through this in the detail that you have and your being as open minded as you have. Right now, my open mindedness is having a bad day but I will resume normal service as and when.
I should like to have got this all horribly wrong and for there to be some benignant explanation that decouples GW from GHGs. As I see it, the counter arguments make matters worse.
Thanks
Alex
“the climate is chaotic to a degree that permits all possible outcomes”, does tend to sensationalize the uncertainty. The impact of internal variability is interesting and non-linear to some extent. Where heat is moved and how quickly, does impact net forcing to different degrees. The short time length and uncertainty in the OHC makes it challenging to determine how strong or how non-linear the impacts are. An open mind would be a good thing faced with the complexity.
Issac,
In the 50year period of warming in your model run without external forcing is it possible for you to workout what caused that excursion? E.g. was it an extended period of el ninos like we had from mid-70’s to late-00’s, was it an extended period of low volcanic activity, was it a certain phase of the Atlantic circulation, or maybe something else or a combination of some/all of these? Does the mix of ‘internal variability’ look like the mix of ‘internal variability’ we’ve had for the past 50 years? If you looked at other periods in a computer run with similar warming trends would they all have the same spatial pattern as the one you investigated, is it possible that some might more closely resemble the spatial pattern of the observed data?
It seems a little unsatisfactory to conclude anything from the fact that one 50 year period in a model run did not resemble observed data.
I mentioned this detail of the low frequency variability in the control simulation of a GCM just to make the point that the strength of the radiative restoring on internal variability could be weaker than that for the forced response, making it harder to constrain the fraction of the trend due to internal variability from the sign of the heat flux alone. I’ll write about the structure and amplitude of low frequency variability in models in another post, as promised above.
The pattern in this particular 50-yr trend in the control is qualitatively similar to the generic very low frequency variability in this particular model, with maximum amplitudes in the subpolar oceans. The question of whether it resembles the internal component of the observed variations is difficult, since the answer requires a convincing extraction of the internal component from the observations, an active area of research.
Issac,
I’ve heard it mentioned that there is some evidence of heat accumulating in the ocean deep below the ARGO network’s range. I performed my own analysis of the ARGO data and the “picture I painted” indicates this is true. Basically, I calculated the temperature trend for each gridbox between 60N and 60S, averaged the longitudinal values, and plotted a scaled image by latitude and depth. The image shows strong warming between ~40-50 degrees North and South, cooling between ~20-30 N/S, and warming in the tropics. The picture is pretty much the same between 300M – 2000M, except a pooling of heat poleward of 40N below 1200M. Here’s a link to a couple of the plots:
https://web.archive.org/web/20191007165314/https://sites.google.com/site/climateadj/argo-analysis
I then compared this image to the A1B scenario model output (10 individual models, first time-series file) and CM2.1 was the only one, in my uninformed opinion, that painted a similar picture.
My questions are:
1) Is it expected that this picture will persist? I only had ARGO data for 2005-2010 so it could be a short term oscillation.
2) Is this the result of increased overturning? To my untrained eye it looks like the heat is increasingly being sucked into the deep at the mid-latitudes.
Reading your previous post about the westerlies shifting poleward made me think of something. I had previously generated a similar image of mean temperatures. This picture shows a dome of warm water encapsulating the relatively cooler water in the tropics:
https://sites.google.com/site/climateadj/argo-sine-fitting/sine-mean-argo.png
This dome extends out to about 40 degrees in both hemispheres. My trend analysis shows the warming of the waters outside the dome and the cooling of the waters that comprise the dome. Could it be that the poleward shift in the westerlies is also shifting the stirring of the heat into the ocean poleward as well?
The ARGO data is an accessible resource for getting a feeling for the structure of the ocean temperature and salinity fields, but I would recommend grabbing an introductory book on climate or oceanography to help you place what you are computing into context. The domes you refer to are the basic structure of the wind-driven thermocline, which is deeper in the subtropics than elsewhere due to the convergence of surface waters due to the north-south “Ekman drift” generated by the Coriolis force and the east-west wind-stress. The shape of the thermocline will definitely adjust to any large-scale shift in the wind field.
Using 5 years of data to define a trend in the the spatial structure of the ocean with depth is unlikely to provide a meaningful comparison with models that are not initialized with the details of the observed ocean state. Comparing to models with initialized states, ie attempts at decadal prediction, would be more interesting. A lot of runs of this type will become available in AR5.