NOAA GFDL - Geophysical Fluid Dynamics LaboratoryGFDL - Geophysical Fluid Dynamics Laboratory

3. The simplicity of the forced climate response

Posted on March 5th, 2011 in Isaac Held's Blog

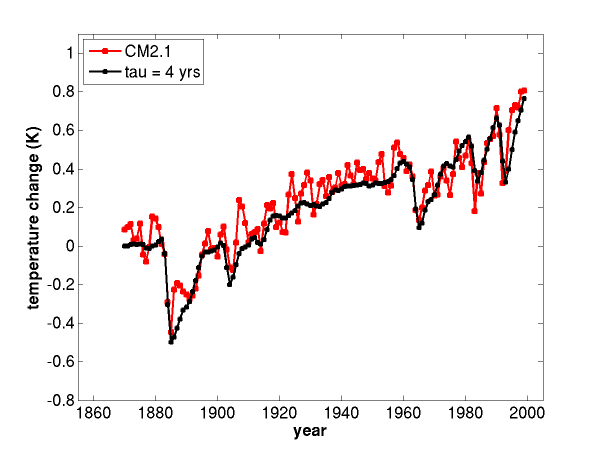
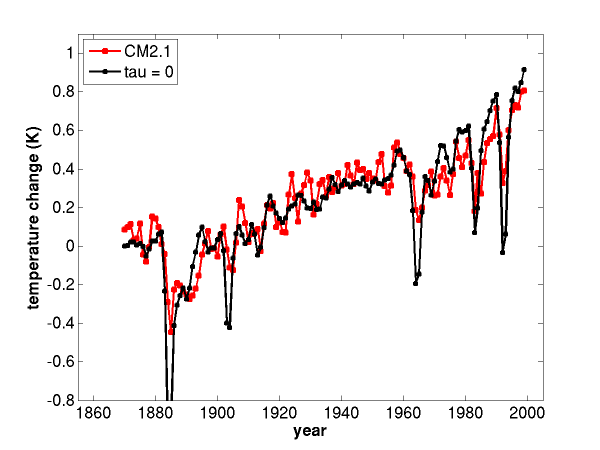An estimate of the forced response in global mean surface temperature, from simulations of the 20th century with a global climate model, GFDL’s CM2.1, (red) and the fit to this evolution with the simplest one-box model (black), for two different relaxation times. From Held et al (2010).

When discussing the emergence of the warming due to increasing greenhouse gases from the background noise, we need to clearly distinguish between the forced response and internal variability, and between transient and equilibrium forced responses.   But there is another fundamental, often implicit, assumption that underlies nearly all such discussions: the simplicity of the forced response. Without this simplicity, there is little point in using concepts like “forcing” or “feedback” to help us get our minds around the problem, or in trying to find simple observational constraints on the future climatic response to increasing CO2. The simplicity I am referring to here is “emergent”, roughly analogous to that of a macroscopic equation of state that emerges, in the thermodynamic limit, from exceedingly complex molecular dynamics.

I’ll begin by looking at some results from a climate model. The model (GFDL’s CM2.1) is one that I happen to be familiar with; it is described in Delworth et al (2006). This model simulates the time evolution of the state of the atmosphere, ocean, land surface, and sea ice, given some initial condition. The complexity of the evolution of the atmospheric state is qualitatively similar to that shown in the videos in posts #1 and #2, although the atmospheric component of CM2.1 has lower horizontal spatial resolution  (roughly 200km).  The input to CM2.1 includes prescribed time-dependent values for the well-mixed greenhouse gases (carbon dioxide, methane, nitrous oxide, CFCs) and other forcing agents (volcanoes, solar irradiance, aerosol and ozone distributions, and land surface characteristics). The model then attempts to simulate the evolution of atmospheric winds, temperatures, water vapor, and clouds; oceanic currents, temperature, and salinity; sea ice concentration and thickness; and land temperatures and ground water.  It does not attempt to predict glaciers, land vegetation, the ozone distribution, or the distribution of aerosols; all of these are prescribed.  Different classes of models prescribe and simulate different things; when reading about a climate model it is always important to try to get a clear idea of what the model is prescribing and what it is simulating.

Holding all of the forcing agents fixed at values thought to be relevant for the latter part of the 19th century and integrating for a while, the model settles into a statistically steady state, with assorted spontaneously generated variability, including mid-latitude weather, ENSO, and lower frequency variations on decadal and longer time scales. Now perturb this control climate by letting the forcing agents evolve in time according to estimates of what occurred in the 20th century. Do this multiple times, with the same forcing evolution in each case, but selecting different states from the control integration as initial conditions. Average enough of these realizations together to define the forced response of whatever climate statistic one is interested in. (One might want to call this the mean forced response. There is more information than this in the ensemble of forced runs, but let’s not worry about that here.) Each realization from a particular initial condition consists of this forced response plus internal variability, but I want to focus here on the forced response. Observations are not expected to closely resemble this forced response unless the internal variability in the quantity being examined is small compared to the variations in the forced response.

The red curve in the figure is an average over 4 of these realizations of the annual mean and global mean surface temperature.  A bigger ensemble would be needed to fully wash out the model’s internal variability (CM2.1 has the interesting problem that its ENSO is too strong).  Volcanoes are the only part of the forcing that has rapid variations; besides these impulsive events, the impression is that the forced response would be smooth if estimated with a much bigger ensemble.

The black curve is a solution to the simplest one-box model of the global mean energy balance:

c \,dT/dt \, = - \lambda T + \mathcal{F}(t)

where \mathcal{F}   is the radiative forcing, \lambda is the strength of relaxation of surface temperatures back to equilibrium, and c a heat capacity.  The global mean temperature T is the perturbation from the control climate.   Where does \mathcal{F} come from?  Here we follow the approach labeled \mathcal{F}_S   in Hansen et al (2005);  it is the net energy flowing in at the top of the model atmosphere, in response to changes in the forcing agents, after allowing the atmosphere (and land) to equilibrate while holding ocean temperatures and sea ice extent fixed.  That is, we use calculations with another configuration of the same model, constrained by prescribing ocean temperatures and sea ice, to tell us what “radiative forcing” it feels as a function of time. This estimate is sometimes referred to as the “radiative flux perturbation”, or RFP,  rather than “radiative forcing”, especially in the aerosol literature, but I think it is the most appropriate way of defining the \mathcal{F} to be used in this kind of energy balance emulation of the full model.   (Why do we fix only ocean and sea ice surface boundary conditions and not land conditions? This is an interesting point that I will need to come back to in another post.)  This estimate of the forcing \mathcal{F} felt by this particular model increases by about 2.0 W/m2 over the time period shown.

The relaxation time, \tau \equiv c/\lambda, is set at 4 years for the plot in the upper panel, a number that was actually obtained by fitting another calculation in which CO2 is instantaneously doubled,  which isolates this fast time scale a bit more simply.  Not surprisingly, being this short, decreasing this time scale by reducing the heat capacity, or even setting it to zero, has little effect on the overall trend over the century; all that happens is that the response to the volcanic forcing has larger amplitude and a shorter recovery time (conserving the integral over time of the volcanic cooling — as one can see from the lower panel, where the black line is simply \mathcal {F}/\lambda).  Other than for the volcanic response, the important parameter is \lambda . The best fit to the GCM’s evolution is obtained with \lambda \approx 2.3 W/(m2 K). (To get a time scale of 4 years with this value of \lambda , the heat capacity needs to be that of about 70 m of water.)

If we compute the forcing due to doubling of CO2 with the same method that we use to compute \mathcal{F}(t) above, we get 3.5 W/m2, so the response to doubling using this value of \lambda would be roughly 1.5 K.  However, if we double the CO2 in the CM2.1 model and integrate long enough so that it approaches its new equilibrium, we find that the global mean surface warming is close to 3.4 K..  Evidently, the simple one-box model fit to CM2.1 does not work on the time scales required for full equilibration. Heat is taken up by the deep ocean during this transient phase, and the effects of this heat uptake are reflected in the value of \lambda in the one-box fit.  Longer time scales, involving a lot more that 70 meters of ocean, come into play as the heat uptake saturates and the model equilibrates.   I will be discussing this issue in the next few posts.

Emulalting GCMs with simpler models has been an ongoing activity over decades. Most of these simple models are  more elaborate than that used here and typically try to do more than just emulate the global mean temperature evolution of GCMs (MAGICC is a good example).  Not all GCMs are this easily fit with simple energy balance models.  In particular, different forcing agents can have different  efficacies, that is, they force different global mean surface temperature for the same global mean radiative forcing (Hansen et al (2005)).

Additionally, there exist components of the oceanic circulation with decadal to multi-decadal time scales that have the potential to impact the evolution of the forced response over the past century.  (This is a different question than whether this internal variability contributes significantly to individual realizations.)  I would like to clarify in my own mind whether the ability to fit the 20th century evolution in this particular GCM with the simplest possible energy balance model,  with no time scales longer than a few years, is typical or idiosyncratic among GCMs.  Other GCMs may require simple emulators with  more degrees of freedom to achieve the same quality of fit.  There is no question that more degrees of freedom are needed to describe the full equilibration of these models to perturbed forcing, as already indicated by the difference in CM2.1’s transient and equilibrium responses described above, but my question specifically refers to simulations of the past century.  I would be very interested if this is discussed somewhere in  the literature on GCM emulators. The problem seems to be that accurate computations of the RFP’s felt by individual models are not generally available.

Forced, dissipative dynamical systems can certainly do very complicated things.  But you can probably find a dynamical system to make just about any point that you want (there may even be a theorem to that effect); it has to have some compelling relevance to the climate system to be of interest to us here.  We will have to return to this issue of linearity-complexity-structural stability, and the critique of climate modeling that we might call “the argument from complexity”, the essence of which is often simply “Who are you kidding? — the system is far too complicated to model with any confidence”.

In the meantime, the goal here has been to try to convince you that the transient forced response in one climate model has a certain simplicity, despite the complexity in the model’s chaotic internal variability. (Admittedly,  we have only talked up to this point about global mean temperature.)  But is there observational evidence for this emergent simplicity in nature? In the limited context of fitting simple energy balance models to the global mean temperature evolution, convincing quantitative fits are more difficult to come by due to uncertainties in the forcing and the fact that we have only one realization to work with.  Fortunately, we have other probes of the climate system.  The seasonal cycle on the one hand and the orbital parameter variations underlying glacial-interglacial fluctuations on the other are wonderful examples of forced responses that nature has provided for us, straddling the time scales of interest for anthropogenic climate change.  In both cases the relevant change in external forcing involves the Earth-Sun configuration, and we know precisely how this configuration changes.  Both have a lot to teach us about the simplicity and/or complexity of climatic responses. Some of the lessons taught by the seasonal cycle are especially simple and important.  Watch out for a future post entitled “Summer is warmer than winter”.

[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]

9 thoughts on “3. The simplicity of the forced climate response”

  1. Hi Isaac – excellent post! You articulate clearly some basic questions about the use of simple models to emulate GCMs that I’d been puzzling about (in a woolly fashion) for some time. I look forward to future posts on this topic.

    Keep up the good work on the blog – I think it’ll provide a valuable resource for the climate-science community!

    David

  2. Why would I want to build a simple model that fits to a GCM? Shouldn’t I be trying to fit to actual climate?
    I don’t like how this modelling appear to be an effort in curve fitting and getting the right anser,a nd then claiming it is just simple physics.

    1. Mike, this is an important point. Modeling a model does seem like a strange thing to do! But I would argue that it is sometimes useful to take a “theoretical stance”, and try to understand ones theory/model. This understanding must translate eventually into more satisfying confrontations with data if it to make a contribution to science, but this can be a multi-step process. Apropos of this blog, I tend to work on the theoretical side of things, and not every post will involve model-data comparisons. So you may need to pick and choose to avoid getting upset — for a post that does involve comparisons with data, see #2.

      Fitting simple models to a GCM should make it easier to criitique the GCM (or at least that aspect of the GCM that is being fit in this way) since one can critique the simple model instead. But, as you say, this fit in itself says nothing directly about nature.

      1. Thanks for the response. I have a bigger issue with the GCMs themselves than a simple theoretical model.

  3. Dr Held,

    Firstly my thanks goes to you for your contributing of these short essays.

    I should also like to discuss simple models as I feel they are commonly neglected on the knee jerk assumption that things are more complicated than that, (perhaps your: “Who are you kidding?” point). Well things really are more complicated, but that does not mean that certain observables are intractable to simple approaches to explanation.

    In order to give my thoughts a wider audience I will spell out a number of concepts, so please do not think I seek to teach you how to suck eggs, or infer that I doubt your familiarity with the mathematics.

    Arguing from simplicity, I will assume that the relationship between an input, a historic flux series and its response, a global temperature anomaly series, can be represented as being that produced by an LTI (linear time invariant) system. Such a system although limited does encompass most of the simple thermal models that occur in the literature, specifically the “red” or slab ocean models, but also others, e.g. “pink” purely diffusive ocean models, and also time invariant upwelling diffusive oceans with or without a surface mixed layers.

    For LTI systems the response (temperature series) is just the convolution of the input (impulse) series with an appropriate response function. The response function containing the model characteristics, e.g. slab, diffusive, etc.. (Convolution being just a fancy term for the type of integration required).

    A good place to start with such a model would be to determine an appropriate response function. This is perhaps more easily done in the case where we seek to emulate a climate simulator (as you have done), and then progress to argue about the real world. Also the simulated data does not suffer from instrumental noise in its observations of the temperature series.

    Here I think that the availability of control run (unforced) data is key. Knowledge that the flux series was unforced allows arguments to be made more directly from the spectral content of the temperature series.

    Again I appeal to simplicity; in the hope that the implied flux series that results from deconvolution of the temperature series and a candidate response function has a simple form. I pick iid gaussian white noise as the required input flux series.

    One can now argue that the spectrum of the simulator’s temperature series has the properties of the frequency response of the filter corresponding to the response function.

    I have looked at HADGem pictrl data (actually the ocean masked data available from Climate Explorer) and the best candidate is a mixed diffusive with a surface mixed layer ocean, which is hardly surprising, but one with a very thin SML, which is puzzling but as I am trying to emulate I have to accept what the analysis suggests the emulator properties are. So I find the spectral properties of the temperature series are essentially “pink” not “red”.

    This means that according to my interpretation of the spectral evidence my simplifying assumption, e.g. iid noise, is equivalent to the assumption that the thermal properties of the system are well modelled by a primarliy diffusive ocean. So evidence that oceans are primarily diffusive would remove my need to appeal to simplicity, some such evidence is in the literature.

    With a little effort I can convert the response function to a function that would give me not the temperature response, but of the OHC response, and were the OHC data available for the CMIP3 simulator runs I could estimate the mean effective (eddy) diffusion coefficient, sadly this is not the case so I can’t. But this will change for CMIP5 I believe.

    My speculative temperature response function is not in its final form. The conductance into space, the ratio of the variation of net TOA flux with that of the surface temperature has been ignored. In terms of the filter this would show as a flattening of the filter characteristic at low frequencies. Given a long enough control run, and sufficient control runs, the characteristic frequency of the deviation from the pink high frequency response could be estimated, and even if the diffusion coefficient remained unknown the relationship of the conductance to the diffusivity could be determined, the response function would then be known upto a scaling factor. Sadly the control run data available to me do not have a long enough historic record, the approach requires millennial scale runs, in my opinion.

    Now that is all well and good in terms of a worked example of using LTI theory to emulate a simulator but it does not justify the simplifying assumption that prompted the use of LTI in the first place.

    Now I cannot see that it is possible to prove that simplification works, but the question can be asked as to whether it can be shown not to work. A sure failure would result if the control run temperature series were not stationary, this could be investigated. Another would be if the series could be shown to be chaotic and not solely stochastic, again a technical challenge. It is likely that ENSO would fall into this second type of failure, but a weaker argument could be made to the effect that ENSO was not distinguishable from uncoupled resonances driven by noise, implying that a filter containing resonances in the ENSO band would pass the test of being statistically indistinguishable.

    What I have hoped to show is that LTI emulators can be developed from data in a methodical way. Also that it allows the characterisation of the response function without recourse to matching forcing fluxes to forced responses, as it can be done with unforced data. This property allows the forced response/forcing data pair to be validated to be a match, as the parameters are already determined from multiple runs with unforced data. Alternatively one may deduce the forcing from the response by deconvolution.

    Importantly LTI gives us techniques for establishing the statistics of both long and short term variability in the emulator. Should one wish to know the chances of a pattern like the PDO, it is a matter forming the convolution of the PDO function with the response function and scaling by an amplitude for the iid noise. The same is true for any other function such as a 30 year linear trend. For such a function a convolution can be formed and a amplitude probability distribution for the spontaneous production of such a trend derived.

    Simple models are analytically powerful and provided they can pass a test for being indistinguishable can be used with some justification until proven otherwise. It seems to be broadly true that in the restricted case for global temperature anomalies, the series are indistinguishable from stochastic ones.

    LTI system theory is well developed, we know the eigenfunctions involved, it is open to discretisation approaches, it encompasses the full range of LTI thermal models by definition, so it is not limited to simple unique time constant approaches, and its statistical properties are well understood, and damnably it seems to work and given the uncertainties of the real world data to come up with much the same vagueness in the all important conductance parameter (from which we can infer the linear component of the climate sensitivity) as do more sophisticated techniques; in my opinion.

    Well that is my paean to simple models, they may be simple but they are not vacuous.

    I look forward to coming back here again soon.

    Alex

  4. In the article you say “I would like to clarify in my own mind whether the ability to fit the 20th century evolution in this particular GCM with the simplest possible energy balance model, with no time scales longer than a few years, is typical or idiosyncratic among GCMs.”

    It appears to be typical, with the typical transient response sensitivity being in the 3.1 to 3.5 W/(m2 K) for CM2.1, GISS E, and CCSM3.

    Willis Eschenbach, over at Watts Up With That has fitted this same simple 1 box model to GISS E and to CCSM3.
    Life is like a black box of chocolates looks a the CSSM3 forcings, converts their forcings from amounts of aerosols to radiative forcings, and fits the model. He did adjust the volcanic forcings by a factor of 0.93 for best fit. Correlation of 0.995 for his toy model to the CSSM3 model. Lambda of 0.32, tau of 3.07 years. As I understand his calculations the inverse of his lambda or 3.125 is what corresponds to your 3.5 watts M-2 K-1.

    In “Zero Point Three times the Forcing” he finds that simply multiplying the GISS E forcings by 0.3 emulates the global average temperature output of that model with rms error of 0.05C. Adding a short lag term improves r^2 to 0.95. He didn’t give the optimal lag time in that post, but over at Climate Audit, the work was duplicated in programming language R.

    The introduction to that post by Steve McIntyre refers back to your blog, as well as MAGICC emulator of Wigley and Raper.

    So for GISS 0.3 C/(watt/m^2) = 3.33 watts/m^2 per C. Willis uses 3.7W/m^2 as the forcing for a doubling of CO2, so end up with 0.3*3.7 = 1.1C/doubling of CO2 as the short term response of the GISS E model.

    That finding is also consistent with the short term response of GISS E being 40% of the long term equilibrium sensitivity, as shown in Hansen’s recent white paper on energy balance. (And only about 60% of long term equilibrium at 123 years after the step). See figures 7 and 8, pages 18 and 19 out of 52. Your work is also mentioned by Hansen in the discussion of those figures.

    1. I haven’t had time to catch up on Hansen’s recent draft paper nor the blog posts that you mention, but the effective transient sensitivity here is 2.3 W/(m^2-K), not 3.1-3.5.

      1. “effective transient sensitivity here is 2.3 W/(m^2-K) not 3.1-3.5”.

        I see where I misread the your blogpost. I should have known that 3.5W M-2 K-1 was not the right number, because of your Held et al 2010 fig 1 that showed short term sensitivity to doubling of about 1.5K.

        It’s obvious now that in the above post that “this value” in “If we compute the forcing due to doubling of CO2 with the same method that we use to compute mathcal{F}(t) above, we get 3.5 W/(m2 K), so the response to doubling using this value of lambda would be roughly 1.5 K. ” refers to the 2.3 W/(m2 K) best fit value from the previous paragraph.

        If I now understand the statement correctly (and that’s remains to be seen), the 3.5W/(m2 K) is a typo and should actually have the units of a forcing, i.e. 3.5W/m^2. Correct?

        Charlie

        p.s. Hansen’s draft is at http://www.columbia.edu/~jeh1/mailings/2011/20110415_EnergyImbalancePaper.pdf
        More of a general review paper for novices like me than a real paper.

Comments are closed.