Posted on May 25th, 2012 in Isaac Held's Blog
Animations of the near surface temperature (top) and upper tropospheric zonal winds (bottom) in an idealized dry atmospheric model. The first 500 days of spinup from a state of rest are shown at one frame per day for the entire globe.
As a change of pace from discussions of climate sensitivity, I’ll describe an idealized atmospheric model that I think of as an important element in a model hierarchy essential to our thinking about atmospheric circulation and climate.
Many of my colleagues are probably tired of hearing me talk about the importance for climate theory of studying a hierarchy of climate models and especially tired of hearing me make the analogy with the hierarchy of model organisms (E. Coli, yeast, fruit fly, zebra fish, mouse, etc) that biologists utilize so effectively. As I have written in a little essay on this subject, biologists have the advantage — their hierarchy is provided by nature, and the conservative character of much of evolution provides confidence that a lot of what we learn from simpler life forms carries over to more complex organisms. Climate theory requires such a hierarchy as well — how else do you go about trying to understand a complex system that you cannot easily perform controlled experiment on? — but we need to construct it ourselves, and agree among ourselves on which idealized systems to study intensively. For a discussion of the atmospheric circulation from the perspective of the insights gained from working with a hierarchy of atmospheric models, see the excellent review by Schneider 2006.
The model I’ll describe here is of a dry atmosphere, an ideal gas on a spherical rotating planet forced only by radiative fluxes — modeled as a simple relaxation of temperature to a “radiative equilibrium” that is a function of latitude and pressure — and a frictional force that relaxes the flow near the surface to zero (in the reference frame rotating with the surface). The model equations are described in Held and Suarez. You can get a feeling for how this and similar setups have been utilized, both for testing numerical methods and for exploring climate dynamics, by googling held suarez idealized gcm.
The model is designed to capture some of the complexity of midlatude jets and storms tracks on a rotating sphere. The climate that emerges (the statistics of the winds and temperatures) has a lot of features that are quite Earth-like. The animations at the top show the near surface temperature and the upper tropospheric zonal (east-west) component of the winds spinning up from a state of rest, using a vanilla spectral model with modest resolution — 20 vertical levels and T42 horizontal resolution — meaning that all fields are expressed as sums over the spherical harmonics with total wavenumber
. Here’s a plot of the time-averaged zonally-averaged zonal winds (zonal => east-west) produced by this model (actually an average over the 2,000 days following the 500 day spinup shown in the animations). The contour interval is 5m/s. The zero contour meets the surface near 30 and 60 degrees latitude.
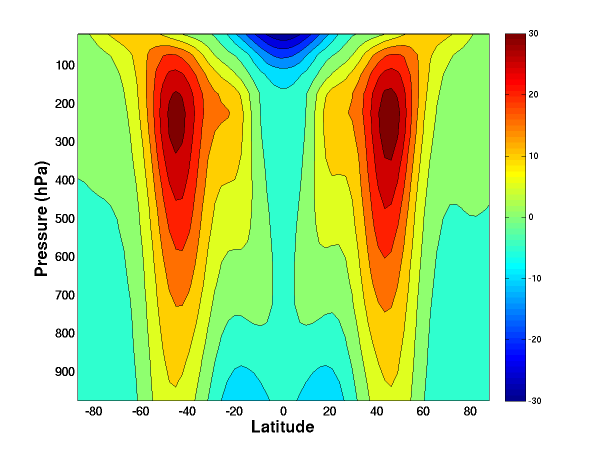 I have starting calling this the fruit fly of climate models. I am not expecting this terminology to catch on, but fruit fly seems about right to me — the model is complex enough to be turbulent and chaotic, with a lot of space and times scales involved, and I think it repays close study, but it is missing many sources of complexity present in the Earth’s atmosphere, and in more comprehensive models. In particular, there are no clouds or even water vapor .
I have starting calling this the fruit fly of climate models. I am not expecting this terminology to catch on, but fruit fly seems about right to me — the model is complex enough to be turbulent and chaotic, with a lot of space and times scales involved, and I think it repays close study, but it is missing many sources of complexity present in the Earth’s atmosphere, and in more comprehensive models. In particular, there are no clouds or even water vapor .
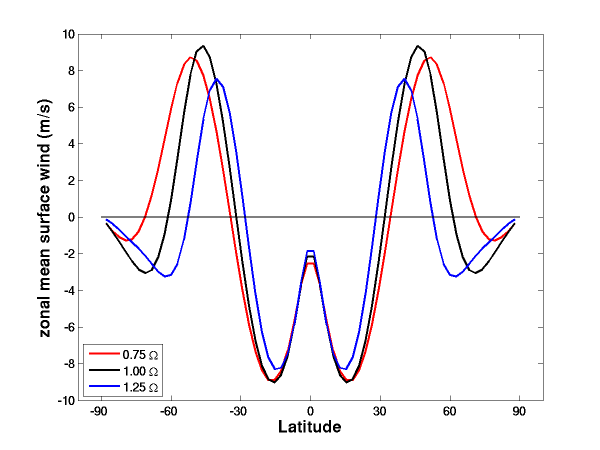
Here’s how the time and zonally averaged winds near the surface change as you increase or decrease the rotation rate by modest amounts from it’s Earth-like value:
The circulation pattern shifts polewards as the rotation rate decreases. The location of the midlatitude westerlies marks the location of the storm tracks, and the transition from easterlies to westerlies in the subtropics marks the region of mean subsidence that generates the subtropical arid zones — in models with water vapor and precipitation. So understanding shifts like these can be important for a lot of reasons. We can think of this problem as a test of our ability to reason about this kind of thing, before tackling the question of circulation shifts in response to global warming.
Gang Chen, Walter Robinson and I looked at how this pattern shifts as the strength of the surface drag is increased or decreased with this same setup in a 2007 paper. The circulation moves polewards as the drag per unit surface wind is reduced — ie, as one makes the surface smoother. We offer an explanation in the paper, but I don’t think we understand it as well as the rotation dependence. The same dependence survives in more comprehensive GCMs — a rougher (sorry – smoother 5/30/12) land surface moves the westerlies and the storm track polewards and decreases polar surface pressures — and is a significant issue when trying to understand model biases and inter-model differences.
If you vary the rotation rate over a larger range in this model, more dramatic things happen. For high rotation rates, the circulation takes on a Jovian appearance with multiple jets in each hemisphere; at very low rotation rates, it looks more Venusian, with a Hadley cell extending from equator to pole and with the upper tropospheric flow resembling solid body rotation at an angular velocity larger than that of the surface (a “superrotating” state). Does this model ever generate bifurcations — abrupt changes in climate at particular values of a parameter? See, in this regard, the new paper by Wang, Gerber, and Polvani. (They modify the model described here in a couple of ways, by changing the radiative equilibrium temperatures and by adding some idealized topography, both designed to create a more plausible stratospheric circulation.) They present evidence for an abrupt change as they warm the upper troposphere of the model.
One way that this model helps me is when I am exposed to a new idea for, say, the time-averaged state of the atmosphere — perhaps for the equator-pole temperature gradient, or the globally averaged kinetic energy generation and dissipation. (For example, there are suggestions that simple variational principles explain these things.) The first thing I do is ask if there is anything in the formulation of the theory that precludes it from being applied to this relatively simple atmosphere-like model. (The fruit fly can’t be used to study immunological responses only found in vertebrates, say.) If not, we can go ahead and test the theory. In my experience, it is often better to be less ambitious and develop and test theories for these turbulent chaotic flows directly, and only after proving them to be useful in idealized contexts make a case for their relevance to the real world.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Wow, I completely agree with you. As a planetary atmosphere student who has also taken a grad-lvl Biology of Aging course (and who has read a lot of papers about mice/C. elegans/Drosophila as model organisms), I’m glad to know that someone else has tried to make the connection between model organisms and atmospheric models.
We have so many different models of model organisms, and in many cases, research that applies to one variant of Drosophila may not necessarily apply to another variant of Drosophila (but it often gets published anyways and ends up in the news, which can really misrepresent things). The same thing also applies to climate models too (though it’s much easier with climate modelling since you don’t have so much genetic drift with climate models). With that all said, I think it’s still very useful when we do rotation rate research with climate models. I did some rotation rate/Hadley Circulation research with CAM3 and even though I would never publish the work given the shortcomings of CAM3 with changing the rotation rate, I still think that the work provides A LOT of interesting/useful information about CAM3 itself.
“Climate theory requires such a hierarchy as well — how else do you go about trying to understand a complex system that you cannot easily perform controlled experiment on? — but we need to construct it ourselves, and agree among ourselves on which idealized systems to study intensively”
Speaking of which, I think that if we could do this, and crowdsource a lot of the work (which wouldn’t be hard to do), we could get A LOT done. Especially since climate modelling research is A LOT cleaner, cheaper, and simpler than biological research, yet it attracts far fewer people for some reason.
Dr. Held – Thanks for this post. I am a big fan of these kinds of stripped down models. Not only can they be used to test a new idea or theory, but they can illustrate/demonstrate fundamental behavior for which the mathematical theory might be somewhat opaque.
For instance, you refer to the possible effects of an altered average pole-equator temperature gradient. Francis and Vavrus (and others) have pointed out that a reduced pole-equator gradient diminishes the geostrophic winds, and assert that this effect “promote[s] higher amplitude and slower moving [Rossby] waves”, with consequences for weather.
I would think that this effect could be readily demonstrated in the model described here, and would be a great tool for public education, a subject of interest to me. I hope you plan to pursue this particular application.
Yes, this does look like a good problem for attack with a hierarchy of idealized models. Does the planetary wave spectrum shift to more quasi-stationary features in response to high latitude warming, resulting in an increase in low frequency climate anomalies? One study on the effects of polar warming in this dry idealized GCM is Son and Lee, 2005, but I do not believe that they looked at the response of the frequency spectrum of planetary waves. On an intuitive level, I would agree that any weakening of upper level winds would likely encourage more low frequency wave activity in this kind of model, by slowing down the eastward phase speeds. But models with zonally symmetric climates, without large scale orographic features like Tibet and the Rockies, and without land-ocean thermal contrasts, produce weak wave activity at low frequencies — so I suspect that this would require a bit more than the fruit fly model. There is likely other work that I am not aware of. If a case could be made for this effect at several levels of a model hierarchy, I think we could return to the kind of observational analysis in this paper with a sharper focus.
Dear Prof. Held,
I always enjoy your educational blog. I am looking for papers or comments about horizontal and vertical atmospheric temperature distributions in a dry and wet atmosphere with and without greenhouse gases at different concentrations.
Best regards
Guenter
Not sure if by “greenhouse gases” you mean “other than water vapor”. In any case, you might try this and references therein
Isaac,
Thanks for this. I’ve studied another paper of yours, the Held and Hou model (from 1981), in a graduate class this last year and did a report on it. The rather simple mathematical expressions that can be used to dissect some of the broad features of the general circulation are quite fascinating, despite the limitations presented by the assumptions used.
One question I had regarding that class of model- I have never really been able to find a physical justification (or perhaps my intuition is just not good) for the dependence of the Hadley circulation width on the global tropopause height, a dependence that clearly emerges in mathematical expressions for the overturning circulation, and that I’ve seen invoked in the literature as an explanation for the observed Hadley expansion during global warming. Could you elaborate on some of the physics here?
In the simplest Hadley cell theories, the flow in the upper troposphere is constrained by the need to conserve angular momentum as rings of air move polewards, while the surface winds are constrained to be small by surface friction, so the vertical gradient of the horizontal wind decreases when the height of the outflow from the Hadley cell rises. This vertical gradient of the horizontal winds is proportional to the horizontal temperature gradient, by what is referred to as thermal wind balance, so this gradient decreases as the vertical extent of the Hadley cell increases. All theories for the extent of the Hadley cell depend one way or the other on the build up of this temperature gradient — the smaller the gradient the more the cell expands, either until it uses up the “available” temperature differential, or until the flow becomes unstable to baroclinic instability.
More formally, both for the simplest steady state Hadley cell theories or theories for the turbulent flow in this dry GCM one can argue that the dependence of the circulation on the rotation rate and on the tropopause height
and on the tropopause height  is primarily felt through the non-dimensional combination
is primarily felt through the non-dimensional combination  , where
, where  is the gravitational acceleration and
is the gravitational acceleration and  is the radius of the planet. So the dependence on rotation rate illustrated in the post is actually very relevant to the sensitivity to the depth of the circulation as well.
is the radius of the planet. So the dependence on rotation rate illustrated in the post is actually very relevant to the sensitivity to the depth of the circulation as well.
But I personally doubt that this is the key to the poleward expansion seen in the comprehensive GCMs in response to warming.
For the non-specialist climate blog fan, it is interesting to try to think about how this and other archetype models might have something to say about the issues discussed on other threads – climate response to GHGs and so on. I put this comment here because Chris – a specialist – went there first! 😉
I was wondering if this sort of model is a good way to try to estimate the no-feedback climate sensitivity (the old version with constant absolute humidity)? I did look in the some of the references and didn’t find an obvious example but I surely could have missed one. Thinking out loud here I guess it could not, at least not without modification, since the incremental RF of CO2 depends on the existing concentration of water vapor in all its 3-dimensional glory (?). So my next thought is to wonder if you hold the absolute WV fixed as a non-condensing greenhouse gas, still under clear skies, how this shifts us along the evolutionary ladder between the fruit fly and a real GCM.
Undoubtedly this model experiment has been done, I just have to find it. Now reading Collins et al 2006: http://onlinelibrary.wiley.com/wol1/doi/10.1029/2005JD006713/full
I believe that you are proposing replacing the idealized radiative transfer in this model (which is just linear damping of temperature back to some specified temperature field) with a real radiative transfer code, but in which the radiatively active constituents are prescribed and not interactive with the model dynamics. I assume that the resulting radiative heating/cooling rates would be used to drive the model — otherwise the radiative transfer calculation is just a post-processing step (from which I doubt that we would learn anything that we don’t already know from inputting observed or idealized profiles into the radiation code). If the realistic radiation is interactive, it is hard to get something that looks reasonably meteorological without including evaporation and condensation of water — the model has to do some non-Earth-like things to balance the tendency of the radiation to strongly destabilize the vertical temperature profile in the absence of evaporation at the surface and condensation in the interior — assuming that the prescribed water vapor and CO2 concentrations in the radiative module are realistic. (One of the tricks in designing this dry fruit fly model is to set up the radiative forcing in such a way that the atmosphere is not destabilized too strongly in the vertical.) Because of this, I and others have gravitated to first including an active water vapor variable before including realistic radiative transfer in these kinds of models.
Continuing that thought, there could be value in a model with passive water vapor and with real radiative transfer using as input this water vapor variable, but with non-interactive radiative fluxes ie, the radiative transfer is just an output that would help you study how changes in the pdf of water vapor as a parameter is changed affect the outgoing OLR — especially the spatial extent of very dry regions.
Bill,
Ming Cai and I did an idealized simulation with a dry GCM, fixed relative (not absolute) humidity and a very idealized surface model, which might of interest to you. No evaporation and condensation were included, but the surface turbulent sensible heat flux in the model is close to the sum of latent heat and sensible heat fluxes in the observations. The dry convective adjustment (I call it “dry” because there is no condensation) restores the temperature profile to the moist adiabat in the tropics, and the relative humidity profile is from GFDL CM2.0 slab ocean run.
The no feedback climate sensitivity was estimated in the paper (Fig.2) in the 3D temperature response to the CO2 forcing (note: the forcing has a vertical structure) in such a way that the radiation fluxes induced by the temperature change exactly balance the CO2-induced radiative perturbation, not only the well-known forcing at the TOA, but also its vertical distribution.
Hope it helps.
Thanks — the “dry adjustment to a moist adiabat” is another option to take the pressure off the resolved circulation to transport all of the required energy upwards, without simulating an active hydrological cycle.
Thank you. I will have a look at this paper, and thank you both for the discussion, it is very helpful.
Dear Prof. Held,
Thank you, a very interesting paper. I have to digest it. Yes I meant other than water vapor.
However, I would be especially interested in the limiting case of a transparent dry atmosphere without greenhouse gases.
Best regards
Guenter
Thanks for posting this. This can help dispel one of the misconceptions about climate models — that we input all the observed data into the model spinup making validation impossible. Recently one engineer I was talking with was incredulous when I said that we could start an atmosphere GCM from an isothermal state, with solar heating and a few butterflies and spin up the general circulation. It really is a profound fact of GFD that is not well appreciated. Although for realism I would like to see a similar spin-up movie for an atmosphere GCM.
Joe, thanks for mentioning the butterflies. This model is being spun up from an isothermal state of rest — plus a little noise to break the zonal (east-west) symmetry, Without the noise, the solution would remain exactly zonally symmetric.
Spinning up a moist model can be a lot more interesting in the tropics, depending on the initial condition for water vapor among other things.
Dear Isaac Held,
Is that “fruit fly model” or are similar simple models open source, and available for download?
How many lines of code does it (grossly) contain?
Does it run stand alone, or is it embedded in some kind of simulation framework which you have to own
and maintain?
Regards,
Marcus
Marcus, the code I use is embedded in what we refer to as our Flexible Modeling System where you can follow the links to downloading the public release of the atmospheric spectral dynamical core. The public release should do this exact calculation out of the box. The code is primarily Fortran90. FMS provides utilities and low-level operations that are meant to hide machine-dependencies from the scientific user. Documentation for this spectral dynamical core can be found here, which refers to this documentation for a shallow water model on the sphere, which in turn refers to this documentation for non-divergent 2D flow on the sphere. I prefer this rather old-fashioned spectral model for idealized studies such as this because the numerics retains exact zonal symmetry. A number of university groups are using versions of this code that typically have branched off from this one in the past and may, in some cases, be cleaner.
The Community Atmospheric Model (CAM) — a part of the Community Earth System Model effort (CESM) also comes with a configuration that runs this same calculation, I believe. CAM, as its name implies, has more user support and a more active bulletin board.
Thank You very much Isaac!
Dear Prof. Held,
How good is this model on the weather scale? Is the relaxation rate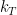 in
in ![\frac{\partial T}{\partial t} =-k_T[T-T_eq]](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Cpartial+T%7D%7B%5Cpartial+t%7D+%3D-k_T%5BT-T_eq%5D&bg=ffffff&fg=000&s=0&c=20201002) set to be 1/40
set to be 1/40  in order to make the model realistic on the weather scale?
in order to make the model realistic on the weather scale?
The model has about the right amount of eddy kinetic energy. And the relaxation time does affect this energy level. Generally speaking, you can’t get a reasonable climate without reasonable “weather-scale” dynamics in mid-latitudes. But Max Suarez noticed the interesting fact early on that the model is too predictable — the error growth in this model is too slow compared to more realistic models (ie, two states that differ very slightly at t = 0 diverge from each other too slowly as time evolves) by something like a factor of 2. I have always assumed that this has something to do with latent heat release, and a couple of people have looked at this over the years, but nothing is published as far as I know.
A couple of months ago I plotted the yearly average zonal mean surface winds for the period 1911-2010 using data from the 20th Century Reanalysis Project V2. I didn’t see much of an expansion of the tropics. Although it wasn’t the focus of my computations, the westerlies appeared to be moving poleward and increasing in velocity.
https://web.archive.org/web/20120921173604/https://sites.google.com/site/climateadj/tropical-expansion?pli=1
People have used a lot of different metrics when looking at “expansion of the tropics”. See, for example, Davis and Rosenlof, 2012