Posted on August 4th, 2012 in Isaac Held's Blog
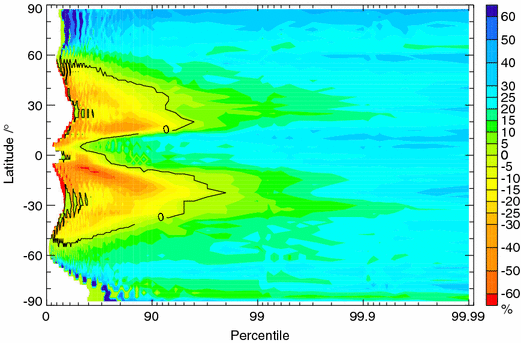
Percentage change in the precipitation falling on days within which the daily precipitation is above the pth percentile (p is horizontal axis) as a function of latitude and averaged over longtitude, over the 21st century in a GCM projection for a business-as-usual scenario, from Pall et al 2007.
(I have added a paragraph under element (1) below in response to some off-line comments — Aug 15)
When I think about global warming enhancing “extremes”, I tend to distinguish in my own mind between different aspects of the problem as follows (there is nothing new here, but these distinctions are not always made very explicit):
1) increases in the frequency of extreme high temperatures that result from an increase in the mean of the temperature distribution without change in the shape of the distribution or in temporal correlations
The assumption that the distribution about the mean and correlations in time do not change certainly seems like an appropriately conservative starting point. But if you look far out on the distribution, the effects on the frequency of occurrence of days above a fixed high temperature, or of consecutive occurrences of very hot days (heat waves), can be surprisingly large. Just assuming a normal distribution, or playing with the shape of the tails of the distribution, and asking simple questions of this sort can be illuminating. I’m often struck by the statement that “we don’t care about the mean; we care about extremes” when these two things are so closely related (in the case of temperature). Uncertainty in the temperature response translates directly into uncertainty in changes in extreme temperatures in this fixed distribution limit. It would be nice if, in model projections, it was more commonplace to divide up the responses in extreme temperatures into a part due just to the increase in mean and a part due to everything else. It would make it easier to see if there was much that was robust across models in the “everything else” part. And it also emphasizes the importance of comparing the shape of the tails of the distributions in models and observations. Of course from this fixed-distribution perspective every statement about the increase in hot extremes is balanced by one about decreases in cold extremes.
(Added Aug 15) The discussion of this topic is often confused by the fact that people are asking different questions. Suppose we consider days that exceed some fixed temperature 
2) increases in extreme precipitation that result from an increase in atmospheric moisture, this increase in turn resulting from the increase in saturation vapor pressure resulting from warming — without changes in the winds that are converging moisture into the region of interest during these extreme precipitation episodes;
There is an important sense in which the increase in high precipitation events is more basic, and more robust, than the changes in the mean precipitation. Some expectations for the latter are discussed in Post #13-14 and include regions of increasing and regions of decreasing mean precipitation. Changes in extremely high precipitation events seem to be simpler — we expect them to increase nearly everywhere. It is precisely when one is strongly converging water into some region, creating a lot of precipitation, that the upper bound on the water vapor in the atmosphere comes into play most strongly. irrespective of what the time mean humidity is doing. If you think of the dominant term that is trying to increase water vapor mixing ratios 
The figure at the top of the page, from Pall et al (2007) illustrates this nicely. Take each grid point in a GCM and create a histogram of daily precipitation. Look at the change in total precip above the p-percentile of precip values, for a particular scenario by the end of the 21st century. To create a smooth zeroth-order picture, sum the p-percentile precip at each point over longitude and then compute the fractional change in the precip amount — as a function of p and of latitude. I like this plot because of the way it distinguishes between the subtropics (where mean precip is decreasing) and subpolar latitudes (where the mean is increasing) — but it does have the disadvantage, if I am interpreting it correctly, that these averaged results are dominated by the high precip regions at that latitude. In subpolar latitudes, precip is increasing in both heavy and light precip events. In the subtropics there is an increase in very heavy precip events (above the 90-95th percentile of daily values) but a decrease when the rainfall values are light. It is the latter that is evidently causing the reduction in the mean, along with an increase in the frequency of dry days not evident in this plot. SREX (Ch. 3) has a summary of observations of trends in extreme precipitation and a lot of references.
3) changes in the frequency or severity of storms or lower frequency climate anomalies, such as droughts, resulting from changes in atmospheric or oceanic circulations on large scales.
An example might be a poleward shift in the Atlantic storm track increasing the frequency of extreme wind and extreme surface wave events on the poleward flank, and decreasing these same extreme events on the equatorward flank of the storm track. These changes in extremes do not result from any subtle change in the underlying dynamics of the storms or waves — the robustness of the changes in extremes depends entirely on the robustness of the large-scale storm track shift.
Another example is the constructive superposition of la Nina and global warming-induced drought over the southern tier of the continental US. Radiative forcing due to increased well-mixed greenhouse gases expands the subtropics and shifts the midlatitude storm tracks polewards in a variety of models of different levels of complexity. El Nino has the opposite effect, especially over and downstream of the Pacific, where it shifts the jet and storm track equatorwards. So the opposite phase of the ENSO cycle, la Nina events, tends to reduce precipitation especially in the southern tier of the continental US (see here). See also this analysis by Bergman et al 2010 of the connections between Pacific ocean temperatures and medieval megadroughts. The la Nina response adds to the simulated effect of the greenhouse gases (here). See also Lau et al 2008 for discussion related to this superposition. By the same token, some of the effects of El Nino events on North America due to the changes in atmospheric circulation might be ameliorated. Even if the meteorology turns out to be basically a linear superposition, impacts of various kinds — forest fires, agricultural, etc, — will remain a source of strong nonlinearities. It is the existence of these nonlinearities in impacts that makes this constructive interference for US drought between la Nina and warming important, even if the effects of warming on the ENSO variability itself turn out to be modest.
Finally, we have–
4) Changes in the intensity of storms.
There is a tempting hand-waving argument that storms will intensify because there would be more heat of condensation released in rising air, creating more buoyancy and stronger upward motion, but there are a variety of reasons why this is not a convincing argument. In any case, you have to distinguish between extratropical storms and tropical cyclones — these have such different dynamics that they present us with two very different sets of problems. I’ll try to get back to some of these eventually. My point here is just to emphasize that, as outlined above, there are reasons to expect changes in extremes that do not depend on these changes in storm intensity.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]