Posted on November 25th, 2012 in Isaac Held's Blog
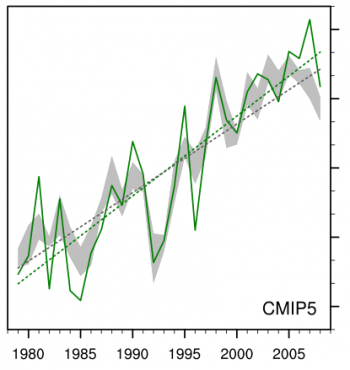Anomalies in annual mean near surface air temperature over land (1979-2008), averaged over the Northern Hemisphere, from CRUTEM4 (green) and as simulated by an ensemble of atmosphere/land models in which oceanic boundary conditions are prescribed to follow observations.
As discussed in previous posts, it is interesting to take the atmosphere and land surface components of a climate model and run it over sea surface temperatures (SSTs) and sea ice extents that, in turn, are prescribed to evolve according to observations. In Post #2 I discussed simulations of trend and variability in hurricane frequency in such a model, and Post #21 focused on the vertical structure of temperature trends in the tropical troposphere. A basic feature worth looking at in this kind of model is simply the land temperature – or, more precisely, the near-surface air temperature over land. How well do models simulate temperature variations and trends over land when SSTs and ice are specified? These simulations are referred to as AMIP simulations, and there are quite a few of these in the CMIP5 archive, covering the period 1979-2008.
The figure at the top summarizes the variation in the Northern Hemisphere mean surface air temperature over land in these CMIP5 AMIP runs. (The figures in this post were generated by my colleague Bruce Wyman.) We compute annual and hemispheric means from the monthly averages in the archive. We first average over all available realizations for each of 17 models. (We have left out two of our own models from this ensemble simply because we generated this figure to have something to compare our results with — adding a couple more models would have little impact on this figure.) The observations, in green, are taken from CRUTEM4. The model results are interpolated to the observational grid and the model results treated in the same way as the observations after that point (including discarding model results at grid points where monthly averaged data is missing.) Anomalies are computed, for each model and the observations, from the mean over the same 1979-2008 period. The shading in the figure indicates the middle half –the 25%-75% percentiles — of the resulting ensemble of values. (Sometimes it is important to focus on the model outliers and the full spread, but here we do the opposite and focus on the core of the model distribution.) The land warming trend in these models is about 15% smaller on average than the observed trend over this period. An example of a study that looks at land temperature trends in earlier AMIP simulations (but extending over the full 20th century) in this way is Scaife et al 2009 . I would like to see more work along these lines.
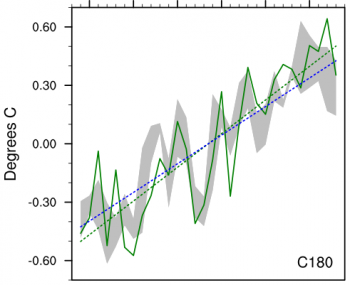
The figure below shows the same result for one of our models, the 50km resolution HiRAM model described in Posts 2 and 21. The shading means something different in this figure. We have three realizations of this model in the archive and the shading shows the spread across these three runs, so it gives you some feeling for the internal variability generated in this statistic by a model with prescribed ocean temperatures and sea ice. This atmospherically-generated internal variability is washed out by averaging over multiple realizations in the figure above. This particular model also underestimates the observed linear warming trend over this period by about 15%. (The grid in this model has the topology of a cube: the “C180″” in the figure indicates that there are 180×180 points on each face of the cube.)
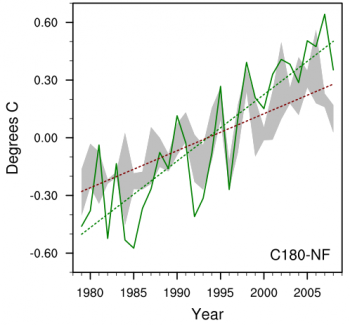
I failed to mention that in these AMIP simulations, in addition to the observed variations in SST and sea ice, one also typically prescribes time-varying “forcing agents”– well-mixed greenhouse gases, aerosols, ozone, solar cycle variations in incoming flux. In some AMIP models aerosol and ozone variations might be predicted, given emissions of precursors, but in the particular model that produces the results above these are all prescribed. (There are no interannual variations in land surface properties such as the type of vegetation in our model at all, and no urban heat island effects.) What happens if you keep all of these forcing agents fixed and vary only the lower boundary condition – the SST and sea ice. The figure below shows what you get from three realizations of this type in the same model. This tells you how much of the land temperature variation and trend is “forced” by the observed changes in ocean boundary conditions versus changes in the forcing agents themselves. In this model, the warming trend over Northern Hemisphere land is reduced by about 30% when holding these forcing agents fixed. Assuming that this is a linear superposition, 70% of the model trend is generated by the communication of the observed oceanic warming to the land.
You have to be a little careful in interpreting this decomposition. Part of the SST and sea ice variation is itself due to the changing forcing, of course. But there are still important things one can learn by comparing this kind of simulation with observed land warming. Suppose that all of of the land warming is just communicated from the ocean, with no direct dependence on forcing agents. Then one can use this fit to analyze what one might call the degree of redundancy of the land temperature record. I use the word redundancy with some reluctance, because it has the connotation of irrelevant whereas I actually mean just the opposite. Redundant climate records are precisely what we need!
On the other hand, to the extent that one can isolate the directly forced component, one can try to use it in attribution studies aimed at seeing whether or not a particular model has, say, the right mix of greenhouse gas and aerosol forcing. For this purpose the hemispheric mean doesn’t give us too much to work with., but there is a lot more information than this in the spatial and seasonal structure of this directly forced component. In particular, one can increase the amplitude of this component by focusing on regions, such as Central Asia, where the oceanic influence is weaker. But it also helps to focus on those regions and times of year when internal (atmospherically-generated) variability is at a minimum (ie summer).
This kind of decomposition of land temperature trends has not received a lot of attention. There are more papers that use AMIP simulations to attribute trends in the atmospheric circulation in this way, such as Deser and Phillips 2009. It would be helpful if this kind of decomposition were available for multiple models in the CMIP5 archive. It would, in particular, be useful to know how robust the spatial and seasonal structure of the fixed “forcing” component is — the more robust this component, the more likely that one can subtract it cleanly from the observed variations and use the remainder to constrain forcing or sensitivity, at least over land.
The value of these AMIP simulations is that one can look in much more detail at the time evolution of the discrepancy between model and observations than is possible when working with a fully coupled model. Consider, for example, the difference between the models’ and CRUTEM4 values in the last few years of this period. Is this due to problems with the land observations, the SSTs and sea ice driving the atmospheric model (we use HADISST), or the models themselves? One interesting point, which I also failed to mention above, is that when one prescribes sea ice in these kinds of AMIP simulations one often just varies ice extent and not thickness, due to the lack of an observational basis for prescribing thickness. ( In contrast, fully-coupled climate models invariably try to simulate thickness variations directly). Could these AMIP models be missing some warming over land due to this deficiency, especially in the last few years of the simulations?
Note added Jan 10: An early paper that introduces the use of AMIP simulations for detection attribution studies that I was not aware of is Folland et al 1998.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]
In the last figure, if you had a model that added back in only the GHG forcing to the land-atmosphere systems, would you expect to see something similar to superimposing the results you get from a model run with fixed SSTs as in post #11 – are they superimposable? If the “sensitivity” of the fixed SST model was 0.35C as indicated (15% of fast feedback response, very roughly) would we be looking at closing about half of the gap between the model and reality in that figure?
Not sure that I follow your argument exactly, but there seems to be an issue here. I have to look at the “no_forcing” runs more closely. From post #11, the global mean land surface warming in response to doubling CO2 is about 0.35C, and if you look at just the Northern Hemisphere it rises to about 0.4 That is a different model than the one considered here, but if anything this HiRAM model has a weaker response — closer to 0.3C over land in the NH. But the greenhouse forcing over this 30 year period is about 1 W/m2, less than a third of doubling. So one would expect only 0.1C or so over this period in a fixed SST model, whereas it looks like at least 0.25C in the figures above. It may be that 3 member ensembles are not large enough to estimate this number, which is pretty small after all, or it might be that there is nonlinearity — I am estimating the response to forcing with fixed SST as the difference between forcing+SST runs and SST only runs.
The second half of your last sentence says what I was trying to say, though I was not looking at the Celsius number, just the percentage contributions. It would be interesting to see what the issue is. Could it be related to the volcanic forcing – since the two major volcanic cooling episodes occurred in the first half of the time interval in your figures, they would be forcing the trend upward?
Also the post seems to assume that SST+ice is a good representation of mixed layer heat content – and perhaps it is; I would expect this from HadSST as opposed to say, Reynolds OI SST – the latter based only on satellite readings and the former including soundings.
The puzzle for me is the rather astounding divergence between land and ocean starting in the late 1970’s. http://www.woodfortrees.org/plot/hadsst2gl/mean:24/from:1900/plot/crutem4vgl/mean:24/from:1900
Such a huge change indicates to me something may not be quite right with the data.
But the CMIP5 models seem to have no difficulty in capturing most of the rapid land warming over this period when forced by the oceanic warming, as shown above. We don’t have runs like these in the CMIP5 archive that go back further — but these do exist for individual models. See also the link to Scaife et al in the post. The changing land/ocean warming ratio can be due to two things from this AMIP perspective — different forcing (ie aerosols holding back the earlier warming more strongly) — or different patterns of ocean warming changing the efficiency of the communication from ocean to land.
Scaife et al used hadcrut3M, which has been replaced by hadcrut4m, where the divergence seems even larger.
http://www.woodfortrees.org/plot/hadsst2gl/mean:24/from:1900/plot/crutem4vgl/mean:24/from:1900/plot/crutem3vgl/mean:24/from:1900 Since 4m is said to be more accurate than the earlier version, I guess that means the 85% of land warming captured by the models in Scaife et al is (based on crut4m) at least somewhat lower than 85% (70%?). In any case, the warming on land from 1900 to ~1975 appears to be closely tracked by ocean warming. The physical reason/justification for such a large divergence post 1975 is not obvious to me.
Steve – you may want to look at that alongside the NH and SH data, as in here. 3 of 4 trends similar to each other throughout, while the NH land diverges widely post 1970s.
Bill,
Indeed. The northern hemisphere divergence post 1975 is difficult to understand considering the relatively rapid rate of atmospheric mixing. I mean, communication between land and ocean ought to be reasonably quick considering the velocity of wind in the atmosphere. Perhaps there is a good explanation for this that I have not seen. The satellite lower tropospheric data show less divergence.
As stated in Isaac’s post, most land temperature warming in model runs is driven by sea surface warming. However, another important aspect of this relationship is that it is not reciprocated – changes to near-surface temperature over land, at global/hemispheric scales, do not have a significant effect on global sea surface temperature.
At the global near-surface level I think one way to picture what’s going on is that there is a conveyor belt transporting heat from the oceans to the land, but not the other way around. If the oceans warm, the land will warm, but if the land warms for some independent reason you shouldn’t expect the sea surface to warm with it.
The difference (land-sea warming contrast) is smaller in the TLT data, probably because the mixing you mention has greater effect aloft, and this is a robust expectation across all model runs. In terms of proportional difference, the observed global land-sea warming contrasts in the lower troposphere and the near surface are a good match for model expectations: in both cases observed land-sea warming contrasts exceed model values.
If the land warming is in a region where the vertical coupling is weak due to the absence of deep convection, say, then you wouldn’t expect it to be communicated efficiently to the oceans by the zonal winds aloft. Is radiative forcing over the oceans more important for land warming than radiative forcing over land is for ocean warming?
Paul S, Isaac,
I am still struggling with a good physical rational for this. For sure warming of the ocean surface should lead to warming over land, but what is the physical explanation for the dramatic amplification of that ocean warming? I remember a group including R. Pielke Sr. published a paper some time ago which suggested much of the enhanced land surface warming of northern latitudes in winter is due to changes in the boundary layer, with less chance of still-air thermal inversions close to the surface, so that the boundary layer temperature remains on average closer to the temperature of the air in the rest of the lower troposphere (were that air to descend to the surface and warm due to compression). This is at least consistent with the observed difference between the trends in the satellite TLT and the land surface. But why has boundary layer changed? Is the influence of increasing GHG’s in the atmosphere (including higher water vapor from those warmer oceans) causing a change in the boundary layer due to reduced radiant surface cooling?
Steve,
Referring to why the AMIP model runs produce similar behaviour, I think it occurs partly due to the specific spatial distribution of SST change over the satellite era and partly because land surfaces are simultaneously being forced by the GHG increase without sharing with the oceans (as depicted in the difference between Isaac’s ‘C180’ and ‘C180-NF’ graphs above).
Taking the HadISST1 dataset and finding a trend for the 30-70ºN latitude band I get 0.2ºC/Decade, compared to 0.08ºC/Decade for 0 – 30ºN and 0.125ºC/Decade average for NH. I selected this band because it contains probably the largest land fraction. So, the land temperatures in this band are responding inline with the local SST trend, which is >2x that of the lower latitude NH. The disproportionate land fraction in this band means land average temperatures are weighted towards this latitude band. To summarise the point, SST warming has occurred over the past thirty years with a spatial distribution which is optimal for enhancing/emphasising NH average land temperature warming.
Isaac showed in a previous post that large continental masses are areas which can warm significantly directly due to forcing, rather than being mostly dependent on SST warming. These continental masses are predominantly situated in the mid-high latitude NH, which is why you would expect a hemispherical difference during transient forcing.
I doubt these two factors would provide a complete explanation but they may account for much of the observed behaviour, at least if the AMIP model runs are providing a reasonable facsimile of the real Earth over the past thirty years.
Hi All,
On the issue of a physical rationale for the amplified warming over land in prescribed SST AGCM simulations: A relevant paper is Compo and Sardeshmukh 2009, “Oceanic influences on recent continental warming” in Climate Dynamics (thanks to Isaac for pointing this paper out to me). They argue that the amplified land warming is driven primarily by increased LW trapping by water vapor over land (their Figs. 2a and 3a).
They do not ascribe this to the canonical fixed RH water vapor feedback (because RH over land does change in their simulations; their Fig. 2d), describing it instead as a “hydrodynamical-radiative” teleconnection causing enhanced water vapor transport from the oceans to land.
They don’t posit a physical explanation for why/how the oceans should transport more water vapor to land when they warm. Could you think of it intuitively as a global-scale sea-breeze? (They also do not discuss changes to the boundary layer, cf. Steve’s comment on the Pielke paper.) I don’t know how well this argument has held up, or if any groups have analyzed in detail moisture transport/circulation changes in AMIP style runs as it relates to this issue.
Hope this contributes to the discussion.
Best,
Spencer
“70% of the model trend is generated by the communication of the observed oceanic warming to the land.”
This is an average for the whole land surface? What would the regional values look like? Presumably coastal US, UK, Western Europe and Japan would be higher than 70%? Can you put a % to any of these regions? There seem to be plenty of studies suggesting the UK temperature is dominated by changes in the Atlantic.
The figures shown are all averages over Northern Hemisphere land. The pattern of trends that you get in these simulations is interesting and not just controlled by proximity to the ocean but also, as a number of papers have discussed, the aridity of the land surface (I’ll try to get back to this point soon). You also have to be careful not to overinterpret trends on small spatial scales that could be affected more strongly by internal variability in the atmospheric circulation than hemispheric or global means.
Regarding the spatial pattern of the land/ocean warming ratio, Sutton et al (2007) have found that there is a significant variation of this ratio with latitude. Typically, there is a local minimum in the deep tropics, maxima in the subtropics, and a decrease to 1 (i.e. equal warming over land and ocean) in mid-latitudes. This latitudinal structure is closely tied to the land relative humidity: Dry land regions exhibit larger surface warming relative to the ocean warming at similar latitudes. In a recent paper [Byrne & O’Gorman (2012)] we introduced a convective quasi-equilibrium theory to estimate the land warming as a function of the ocean warming and the land & ocean relative humidities (the theory was then tested successfully in an idealized GCM). In our theory, the land/ocean warming ratio increases monotonically with increasing land aridity. Furthermore, changes in near-surface relative humidity, which can be substantial over land (~2%/K), contribute strongly to large warming ratios in regions that become more arid under climate model projections (e.g. the poleward flanks of the Hadley cells).
Cheers,
Mike
I enjoyed your post Isaac and now better understand the value of the AMIP simulations.
Regarding the discrepancy between the AMIP models and the observations of land temperatures in the last decade or so, I think surface humidity trends may be playing an important role. Simmons et al (2010) looked at relative humidity over land in the ERA-40 reanalysis and in direct observations (HadCRUH) and found a sharp decrease of ~2% in land RH between 2000 and 2008. Myself and others have proposed that a strong link exists between near-surface temperature and humidity and the observational temperature record over land does appear to show an increase that is roughly in-step with the recent land drying. I have had a cursory look at the AMIP simulations from CMIP5 and they do not seem to capture the marked land drying mentioned above, a deficiency which we would argue leads (partly?) to the underestimation of the land temperatures. It would be interesting to figure out both the cause of this recent land drying, and why the AMIP runs fail to simulate it. Cheers! Mike
thanks — if forced, a drying that kicked in rather suddenly would be a curious and important nonlinearity.
Recently I’ve noticed a large inter-model difference in what I would call the “background” TOA energy imbalance over land, calculated using rsdt – (rsut+rlut) and averaged over the first few years of the model historical run.
Taking two models which appear to be at opposite ends of the spectrum – CCSM4 and CSIRO-Mk3.6 – the values are, respectively, ~ -22W/m^2 and ~ -12W/m^2. To plug the gap and attain a global near-zero imbalance you get the opposite effect over the oceans: ~ +8.5W/m^2 and ~ +5.5W/m^2 respectively.
Given that the AMIP runs use prescribed SSTs, presumably the TOA imbalance averaged over ocean area is somewhat equalised(?), which would have to result in an equalisation of the TOA imbalance over land area, or there would be a large imbalance present in one or other of the simulations. I’m just wondering if this presumption is correct – that both are equalised – and, if so, how to interpret the large inter-model differences concerning this variable.
If you perturb the solar energy absorbed over land, say, a large part of the perturbation will be balanced by export to the ocean. See Lambert et al 2011 or Ming and Ramaswamy 2012. The models presumably have different cloud covers.
Fixing SST does not constrain the flux into the ocean. Fixing SST and fixing flux can be thought of as more or less orthogonal boundary conditions. Fixing SST lets the flux float — fixing flux lets the SST float. In practice, however, models used in fixed SST simulations are also used or planned for future use in coupled models, in which case you need a close global mean TOA balance to avoid severe drift in SSTs — ie, you need near zero flux into the oceans since this is essentially the same as the TOA flux, and the models are developed with this constraint in mind. You should still expect the land-ocean energy exchange to vary between models, given differences in clouds primarily, as you are finding. .
Thanks Isaac,
Completely different question: have you seen any indication of how choice of SST/sea ice dataset influences the resulting land and tropospheric temperature changes? I think HadISST trend over the 1979-2008 period is about 0.075/Dec global average, while HadSST2 and 3 produce ~0.13/Dec.
I think that the dependence on the SST data set driving this kind of model is potentially very important if the goal is to use these runs to help in attribution — ie constraining aerosol forcing or land-use changes. Differences in global mean trends may not capture the main differences – the global or hemispheric land trends could potentially be dependent on the spatial structure of the SST trends. Most obviously, NH ocean trends will be more relevant for land warming than global ocean trends because that’s where the land is. (And trends themselves are not ideal indices with time series in which volcanos play a significant role.) We (colleagues at GFDL) have started looking at the dependence of AMIP runs on the choice of SST boundary condition in another context — that of the trend in Atlantic hurricane frequency in the simulations described in post #2, but haven’t focused on land temperature in this context. We should.
Is it possible to prescribe SST (and maybe other climate variable like trade winds) over the tropical pacific in order to force an ENSO pattern in model outputs that are similar to the real world pattern and force the typical (lagged) global responses to ENSO as well?
Models with prescribed SSTs over the world ocean, like the ones being described here, can easily be manipulated, given some definition of ENSO, to isolate the atmospheric response to ENSO from the remainder. This may be OK for some purposes but not for looking at time lags since these involve the reaction of the rest of the world ocean to ENSO. For that you need at the minimum something like the model pictured in post #18 in which the oceans outside of the Tropical Pacific are allowed to adjust to the atmospheric response to ENSO. But even better would be to just take a coupled model and override the surface wind stress felt by the equatorial Pacific Ocean with observations (reanalyses) or to assimilate observations of surface pressure in the equatorial Pacific (and nothing else) into a free running coupled model. A lot of research with ocean models indicates that all you need to do to get more or less the right ENSO SST evolution is to constrain the surface stress. This approach would allow you to look at the warming trend due to external forcing, even in the equatorial Pacific, and at the same time to constrain the model ENSO’s time series so as to look like that observed — a bit like a coupled version of the 20th Century Reanalysis Project but focused on ENSO only. The definition of “ENSO” in this context would be whatever it is that is constrained in the coupled model by constraining equatorial Pacific surface pressures.
Ok thanks for the response.
I spent a bit of time looking for papers that showed this sort of work but found nothing. Do you know of anybody who has done these sorts of experiments? With the focus on ENSO.
Here is an example of a model with prescribed SSTs in the equatorial Pacific that predicts SSTs elsewhere (and the state of the atmosphere/land). This is used to study how ENSO SSTs influence SSTs elsewhere through an “atmospheric bridge”. I am not aware of anyone who has tried a coupled model with assimilation of surface pressures in the equatorial Pacific, which would be more interesting in the context of SST trend attribution.