Posted on September 23rd, 2013 in Isaac Held's Blog
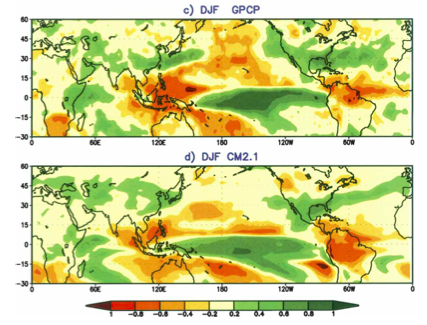 Correlation between seasonal mean precipitation (Dec-Jan-Feb) and sea surface temperatures in the eastern equatorial Pacific (Niño 3.4: 120W-170W and 5S-5N) in observations (GPCP) and in a free-running coupled atmosphere-ocean model (GFDL’s CM2.1), from Wittenberg et al 2006. Green areas are wetter in El Niño and drier in La Niña winters; red areas are drier in El Niño and wetter in La Niña.
Correlation between seasonal mean precipitation (Dec-Jan-Feb) and sea surface temperatures in the eastern equatorial Pacific (Niño 3.4: 120W-170W and 5S-5N) in observations (GPCP) and in a free-running coupled atmosphere-ocean model (GFDL’s CM2.1), from Wittenberg et al 2006. Green areas are wetter in El Niño and drier in La Niña winters; red areas are drier in El Niño and wetter in La Niña.
(Sept 30: I have moved a few sentences around to make this read better, without changing anything of substance.)
It is old news to farmers and water resource managers in the southern tier of the continental US that La Niña is associated with drought, especially with rainfall deficits in the winter months. Since the major El Niño event of 1997-8, our climate system has been reluctant to generate El Niño at the expected frequency and instead the Pacific has seen several substantial La Niña events with mostly near neutral conditions in between. This La Niña flavor to the past 15 years has been identified as causing at least part of the hiatus in global warming over this same period by simple empirical fitting and more recently by Kosaka and Xie 2013, in which a climate model is manipulated by restoring temperatures to observations in the eastern equatorial Pacific. I find the excellent fit obtained in that paper compelling, having no free parameters in the sense that this computation was not contemplated while the model, GFDL’s CM2.1, was under development, and the model was not modified from the form in which it was frozen back in 2005. The explanation for the hiatus must, in appears, flow through the the equatorial Pacific. (I have commented on this paper further here.) These authors mention briefly an important implication of this connection — the extended drought in the Southern US and the hiatus in global mean warming are related.
The figure at the top compares the response of precipitation to ENSO in an observational estimate and in the same climate model as utilized by Kosaka and Xie. This result is obtained with a free-running model, producing its own ENSO variability. (The correlation averages over any asymmetries between warm El Niño and cold La Niña phases, which are not exact mirror images of each other, but does not change the basic picture.) The model evidently generates a reasonable simulation of the precipitation response over the US, justifying the discussion by Kosaka and Xie of the connection to the hiatus. Results such as these are what make the case that global models are of value in estimating the broad-scale changes in precipitation associated with climate change if not, as yet, detailed regional features.
In passing, I just want to put in a good word for the simulation of ENSO in current climate models. This comes in for a lot of criticism it seems, but from my perspective, having been around for a while, I am impressed by how far we have come. ENSO variability develops spontaneously, of course, just like midlatitude storms on much shorter time scales. The ENSO simulation in this model is not without its problems, needless to say. Its amplitude is too strong and the structure has some problems as well, most notably temperature anomalies spread too far westward on the equator in the Pacific, distorting the Indonesian drying among other things. This model was developed a decade ago — we (that is, my GFDL colleagues) are confident that we can do better now (Delworth et al 2012). Are these model’s good enough to simulate the response of ENSO to increasing greenhouse gases or changing aerosols?
When I first started this blog I thought that I would try to focus on things other than the global mean surface temperature time series, but if you are a regular reader you know that I haven’t been very successful at this. And it becomes even harder with the emphasis on the hiatus. But this connection between US drought and the hiatus emphasizes for me how important it is to look at things more broadly, especially when there is more than one thing going on (ie two different kinds of external forcing or external forcing plus internal variability). This model, like most others (see the canonical figure from the AR4 Summary for Policymakers) predicts that increasing well-mixed greenhouse gases will dry the Southwest and South central US. So El Niño and increasing greenhouse gases have the same sign effect on global mean temperature, but opposite effects on rainfall in the Southern US.
We think of the response of precipitation to greenhouse gas forcing as a combination of a part that is controlled by the temperature increase — specifically the increase in water vapor accompanying the temperature increase, as discussed in Post #13 — and a part related to changes in atmospheric circulation. The response to ENSO is mostly due to changes in atmospheric circulation, which have little resemblance to the circulation changes induced by greenhouse gas forcing – in fact they tend to have the opposite character, with the large-scale circulation shifting equatorward rather than poleward with global mean warming — as indicated in the following figure, from Lu et al 2008:
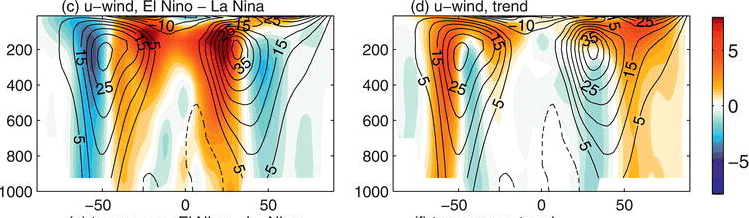 This plot shows results from CM2.1 once again, focusing on the zonal mean (the average around a latitude circle) of the zonal wind (positive if from the west). The contours in each plot are the model’s climatological mean in Dec-Jan-Feb and the colors the change due to ENSO (El Niño – La Niña) on the left and the trend over the 21st century in a projection using the A2 scenario on the right. Red is positive and green negative, so comparing the colors to the climatology, you can see that El Niño moves this entire pattern equatorwards while the model’s 21st century trend, dominated by the response to greenhouse gases, moves it polewards. Flipping the sign on the left to correspond to the La Niña state would make the figures look more similar. The rainfall pattern outside of the tropics goes along for the ride on these circulation changes. There is a lot of literature on the theory for these large-scale shifts in circulation, some of it using variants of the fruit fly model (post #28). One thing these model results are telling us is that global mean warming, or the warming of the tropics in isolation, cannot be the primary reason for these shifts in circulation in general.
This plot shows results from CM2.1 once again, focusing on the zonal mean (the average around a latitude circle) of the zonal wind (positive if from the west). The contours in each plot are the model’s climatological mean in Dec-Jan-Feb and the colors the change due to ENSO (El Niño – La Niña) on the left and the trend over the 21st century in a projection using the A2 scenario on the right. Red is positive and green negative, so comparing the colors to the climatology, you can see that El Niño moves this entire pattern equatorwards while the model’s 21st century trend, dominated by the response to greenhouse gases, moves it polewards. Flipping the sign on the left to correspond to the La Niña state would make the figures look more similar. The rainfall pattern outside of the tropics goes along for the ride on these circulation changes. There is a lot of literature on the theory for these large-scale shifts in circulation, some of it using variants of the fruit fly model (post #28). One thing these model results are telling us is that global mean warming, or the warming of the tropics in isolation, cannot be the primary reason for these shifts in circulation in general.
The magnitudes in this figure are also telling us something. It takes a century of global warming to reach the amplitude of the change in circulation associated with a flip from El Niño to La Niña. This might seem small, until you think about the implications of a shift in the mean comparable to the peak-to-peak variations in the ENSO cycle. Well before this point one would reach a situation in which the shift in the mean is comparable to changes in circulation or rainfall averaged over one or two decades. Whether we are already approaching the latter point is obviously a key question in climate research. The magnitude of the precipitation changes in the US due to an increase in greenhouse gases varies from model to model, so estimates of what role global warming has played in precipitation changes over the US during the hiatus will be model dependent. Some of the inter-model spread here is itself likely to be related to the spread in the response of the equatorial Pacific to greenhouse gas forcing.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac,
The one issue I’ve had with Kosaka and Xie paper is their failure to capture the Eurasian cooling signal in DJF that has been a predominant component of the global trend during the last 15 years. I think it’s a very nice paper that contributes a lot, but I’m a little worried about the overconfidence in the results that people have taken away (in general there have been several schools of thought on the hiatus, whether it be internal variability or external forcing, e.g., Asian aerosols. These aren’t contradictory things but a lot of people seem to claim to have “explained” the hiatus with their favorite mechanism).
There is a lot of internal variability over the continents in Northern hemisphere winter even in “AMIP” simulations in which sea surface temperatures are prescribed over the whole ocean. (I looked briefly at summer over Asia in AMIP runs in a previous post to avoid this variability.) But it’s a large discrepancy. it would be interesting to see if any members of the POGA ensemble have cooling of this magnitude over Asia.
In the Extended Data Figure 3 caption Kosaka and Xie state that energy budget is not closed in POGA-H. From the data shown in that figure it can be seen that this is not a minor deviation but very significant as the change in OHC is in POGA-H very close to HIST, while the net radiative imbalance at TOA is about 30% larger. Evidently all that extra heat is removed from the Eastern Pacific to “a black hole”.
I wonder what one should think about such a breakdown of energy conservation and its influence on the conclusions of the paper.
Furthermore the rate of growth of OHC seems to be rather large in comparison with the empirical data making the discrepancy between POGA-H and empirical data even larger in what concerns net radiative balance at TOA.
Pekka,
This is a confusing issue (I think I managed to confuse myself in a reply to your question a few hours ago, which I have removed to try again.)
The model does not conserve energy when near-surface temperatures in the equatorial eastern pacific are prescribed. You could try to encourage the ocean to transport the needed amount of heat away from the surface in this region, perhaps by instead constraining the horizontal surface stresses on the ocean that force upwelling or downwelling in the tropics — in which case energy would be conserved more accurately — all heat would be accounted for. Suppose this worked, and you could get the ocean to do this transport for you, creating SSTs that matched observations. Would the atmosphere care whether energy was conserved or not? After all, It only senses the SSTs, not the deeper ocean layers. In particular, would the TOA fluxes be different? Distortion would occur because heat would not be transported correctly subsurface (because it has disappeared) out of the prescribed region into the freely evolving part of the ocean model, eventually modifying surface temperatures in those regions. The importance of this distortion is partly a question of time scale presumably. I guess I need to think about this some more. One is fortunate, I think, in that the circulation is predominately converging into this region subsurface, to provide the upwelling waters, and diverging at the surface, so temperature information has a hard time flowing out subsurface.
Isaac,
What you write is in line with my own understanding of what must be going on in the model calculation. That corresponds to the situation where the upwelling water is significantly colder than in the HIST type calculation. But what would be the reason for such a deviation? Could it happen without some other phenomenon in another part of the pacific that has visible effects also on the surface? (My “another” refers to something related to the cause of the cold upwelling flow, not to the consequences present in the actual POGA-H calculation.)
Some people (e.g. have been trying to glean further quantitative conclusions from this experiment by reference to the CM2.1 model details given in AR4, most notably its stated TCR.
I’ve noticed that the mean 1950-2000 warming of the HIST ensemble used here is substantially larger than that produced by the CMIP3 runs of CM2.1. Do you know what the difference is here? Has the model been altered or is the forcing different?
I haven’t compared the HIST ensemble to the CMIP3 runs of CM2.1 myself. Talking to the people who know about this here, the model used for this paper has some minor changes from the CMIP3 model, which I would expect to be in the noise when estimating TCR — but it does not appear that this has been checked explicitly. We think the evolution of the forcing agents prior to 2000, when the CMIP3 runs end, is the same as used in those earlier runs.
The potential for constraining TCR with this kind of simulation is interesting to me as well.
The forcings ARE different — the Kosaka and Xie integrations use CMIP5 recommended forcing agents, which differ from what we used for CMIP3, especially for solar and aerosols.
Hi Isaac,
My concern with fixing tropical Pacific temperatures is twofold: First, like Pekka, I am not comfortable with vast quantities of heat disappearing into a black hole, even if this improves the model’s simulation of the real Earth. The fact that removing this heat makes the model work better fairly well screams something is structurally wrong with the model. Second, are the authors sure that there is anything special about the tropical Pacific? If the tropical ocean surface temperature elsewhere were artificially changed to remove a comparable amount of heat, would that have a similar influence on model performance? The danger with this type of study seems to me to be not asking enough questions about the results.
This question comes up a lot in discussions of this kind of simulation (which has a long history but using mixed layer or simple slab ocean models, ie Lau and Nath 2000, rather than fully coupled oceans). Why not constrain temperatures from the Indian ocean or the western equatorial Pacific rather than the eastern equatorial Pacific? If the model is warming too much in the tropics over the hiatus period, what difference does it make where you remove heat from — or why not remove heat uniformly throughout the tropics. If all you are interested in is mimicking the global mean temperature you could do this in any number of ways. But would the result look like the actual state of the tropics in this period? if you prescribe only the west pacific to be cooler than the model wants it to be, I would guess that you would push the model into an El Nino rather than La Nina state — ie with the wrong sign of the east-west temperature gradient across the Pacific for the hiatus period and the wrong sign precipitation anomalies in and outside of the tropics. That’s my intuition in any case.
Rong Zhang perturbed CM2.1 to mimic observed Atlantic variability by replacing the Atlantic by a slab ocean and prescribing north-south heat redistribution in the Atlantic — see Zhang, Delworth, Held 2007 — with this configuration or something equivalent you can ask if the recent La-Nina-like state in the Pacific could be driven from the Atlantic. Since we are just moving heat horizontally you could argue that this is more energetically consistent than the Kosaka and Xie methodology, but to improve this simulation you have to move heat from the surface to the interior of the Atlantic and not just redistribute horizontally, in which case we would have the same issue. Ideally, as I mentioned above, you want to assimilate observations in a more energetically consistent way.
Hi Isaac,
Thanks for your reply. Please let me try explain my concern a little more clearly: Kosaka and Xie set the eastern/central tropical Pacific to match historical observations… and presumably they understand that with this continuous ‘adjustment’ in ocean surface temperature there is no closure in model heat balance (TOA imbalance does not equal OHC change in the model runs with adjusted sea surface temperatures). Fair enough. But what are the implications of this?
We already know from many publications that ENSO has a very strong and consistent influence on both regional and global average temperatures (and much more, such as precipitation patterns), so when Kosaka and Xie fix the ocean surface in the central/eastern tropical Pacific to the correct values (dictated by ENSO data) they are automatically bound to improve conformity of the model to measured temperatures, precipitation, etc…. no surprise there. (My own estimate is that about 10% of the variation in Nino 3.4 temperature shows up in the global average trend… lagged a bit, of course). LOTS of people have already done much the same via linear regression analysis and concluded much the same. Sam-old-same-old.
But Kosaka and Xie go much further. By forcing the central and eastern tropical Pacific surface temperature to match observations, they do two things: 1) they are automatically accounting for a lot of the global variation (yielding much better model fit to the data), and 2) they are making the heat balance in the model better match the real world heat balance. It is the second which concerns me. When Kosaka and Xie take heat out of the model ‘world’ by fixing ocean surface temperatures, they are masking deficiencies in the model. If the model were truly accurate in heat transport between surface and space (via all possible routes) then the model could not be expected to follow the historical data exactly (it is impossible to match the initial conditions exactly), but the model would not, on average, have a net heat balance error over time… and it (indeed all CIMP models) clearly does.
The widely pronounced conclusion that Kosaka and Xie ‘prove’ the recent slow warming is due entirely to ENSO begs the real issue: the basic model they used does not correctly match Earth’s heat balance. It is clear that at least some of ‘the pause’ is the result of the influence of ENSO (and perhaps other pseudo-cyclical behaviors). My personal guess is that the underlying trend is in the range of 0.11C per decade, and other factors (like ENSO, PDO, AMO, etc.) explain a fair portion of the divergence between models and reality. But it seems to me that at least some of that divergence is due to model error. Kosaka and Xie appear to conclude that ENSO explains all of ‘the pause’. About that I think they are mistaken.
If the model were perfect, with this SST adjustment to observations you would still have an ensemble mean energy source/sink in the POGA-H ensemble since you are forcing the model to follow a particular realization. Since the model and external forcings are not perfect there is also an energy source/sink due to these imperfections. The result you see in a particular model is a combination of these two things. I gather we agree on this. I am personally not sure what the relative importance of these two contributions is in these CM2.1 POGA simulations.
The way I think about the implication of Kosaka and Xie is that it strongly suggests that the explanation for the hiatus must “flow through” the equatorial Pacific, ie A => la Nina-like period in the equatorial Pacific => hiatus, where A might be any number of things, but explanations like A => hiatus that don’t involve the equatorial pacific are disfavored. This leaves open the question of whether the la Nina-like state over this period is forced or internal and, if internal, if its source is the dynamics of the tropical pacific itself or is in part a remote effect of the AMO or the southern ocean or whatever. The authors clearly feel that it is internal and generated in the equatorial Pacific. I think this is a reasonable null hypothesis for this hiatus period but there is a lot of research on this topic going on, so we’ll see. This hypothesis can be true whatever the imperfections of a particular climate model.
Hi Isaac,
It seems to me recent papers about global warming hiatus mainly put the focus on La-Nina-like phase of IPO (Meehl etal 2013, Kosaka and Xie 2013, and the recent paper by England et al. 2014).
On one hand, I generally agree with these researches about the importance of equatorial Pacific in the hiatus based on my experience with NCAR’s CCSM3 simulation.
On the other hand, I also felt the role of AMO might be overlooked by the use of running 11-yr-trend of global-mean SAT. In one set of equilibrium coupled CCSM3 simulation, the running 11-yr-trend is highly correlated with PDO index (0.42 for 290 years), while the correlation is almost 0 between the the running 11-yr-trend and AMO index. These are very consistent with the results from Meehl et al 2011 and Kosaka and Xie 2013, even our result is based on an equilibrium simulation.
However, if we just do a running-average over the global SAT itself (not the trend), then the correlation between 11y (or 31yr)-running mean of global SAT and the AMO index is 0.59 ( or 0.62) with the sample being about 300 (yrs), i.e., the fluctuation of global-mean SAT (about 0.2 degrees in the simulation) is highly correlated to AMO. If we suppose the actual fluctuation of global SAT in reality due to AMO is also 0.2 degrees, and the period of AMO is about 60 years, then in some decades ( during transition from the positive peak to the negative bottom) the trend of global SAT (over time scale of 11yr~31yr) could also reach about -0.6 ~ -0.7 degree/decade, which might mean a global warming hiatus if we take the forced trend as 0.7 degree/decade. My results were based on one model, and I am not sure if it is the case or not for observation and other models.
But my impression obtained from CCSM3 is that AMO might be important to the duration of hiatus if not to the on-set of hiatus, and a hiatus longer than 15-years might be possible if the transition from positive AMO to negative AMO also could cause a fluctuation of 0.2 degrees in global-mean SAT.
Kevin Trenbirth has stated the ocean absorbing an extra 0.5 W/m2 in the last 15 or so years and heating the deeper oceans is the cause of the hiatus. I do not see how the oceans could all of a sudden absorb more unless the solar intensity changed, or the albedo changed. Either case would also result in more land heating and near surface heating also. The movement of near surface (0-700m) ocean currents that produce ENSO effects (ElNino and LaNina, and the long period PDO and AMO can temporarily add or subtract surface energy enough to change surface temperature for fairly long periods. However, the 15 year hiatus has been blamed on deeper ocean heat increase (~8E22 J/decade) being stored down to 2000 m, and the claim is made that this will eventually come back and be released to boost heating at some later date. I have no problem with the near surface effects, but calculating the temperature rise at the larger depths indicates only about 0.2C /century for the indicated rate. Besides the point that very deep ocean flow take centuries or longer to circulate and for eventual upwelling, the problem is that heat transfer does not care what the source energy content is (for very large sources), it only cares what the driving temperature difference is. Thus the maximum added effect of the large accumulated energy is to add a MAXIMUM of about 0.2C per century to the mean air temperature. Is this argument too simplistic, or is the confusion between energy content and what drives heat transfer the reason such claims are made?
I have to learn more about this deep heat content increase. Presumably true irreversible heat transfer could only occur to this depth on this time scale in deep or intermediate water formation regions in the subpolar oceans. But the heat content below some depth can also change simply due to the deformation of constant density surfaces due to the wind or more generally as an adjustment to what is happening to the density field above this level. This is completely and rapidly reversible when these density surfaces return to a less deformed shape. Oceanographers try to remove this effect to focus better on the more irreversible component of the heat redistribution by doing a census of waters with different densities. Is the mass of water between specified density values changing systematically or is it just that the boundary between different density layers is deformed adiabatically? The latter would have little relevance for the surface. I haven’t seen this kind of analysis for these recent observations.
Your intuition would be right, I think, if this heat content change were fairly uniform over these deep layers and were due to true mixing or transport and not to adiabatic sloshing. In post #8, I refer to this effect of deep ocean warming on the surface at a later date as the recalcitrant component of global warming.
If we ascribe the hiatus to a lack of El Nino events in the 2000s, how much of the warming in the 1980s and 1990s do we ascribe to the excess of El Nino events?
Looking at Fig 1 in Kosaka and Xie, in the warming period from 1970 through 1995 I don’t see much distinction between the HIST and POGA-H ensemble means. So in this model response to the observed eastern equatorial Pacific temperatures does not make much difference to the global mean warming. Between 1960 and 1970 the POGA-H run is colder, so if we look at 1960-1995, we might conclude based on this model that there was a modest contribution to the warming from the east pacific –but if we go back to 1950 the two ensembles come together again. You can make up your own mind from the figure.
If you check out Extended Data Table 1, you will see that constraining the temperature in the Eastern Equatorial Pacific (POGA-H) added 0.14 degC of warming during 1971-1997 while subtracting 0.20 degC from warming during the 2002-2012 hiatus. If unexplained behavior of Eastern Equatorial Pacific is the reason for the hiatus, it also amplified earlier warming. Over the whole period, POGA-H predicted 0.54 degC of warming, while HIST predicted 0.60 degC. I suspect that there is no alternative to the conclusion that there is a similar long-term discrepancy between BOTH models and observations, despite the improved correlation with POGA-H. (However, one shouldn’t be drawing any conclusions from these number in the absence of confidence intervals.)
I made a comparison of TOA imbalance with increase of OHC for HIST and POGA-H from the data of Extended Data Figure 3. When the increase in OHC is multiplied by 1.25 it agrees closely with the TOA imbalance in case of HIST, but there’s a sizable difference for POGA-H since 1999. This is the amount of heat that goes to the black hole in POGA-H. Earlier deviations are small in comparison. Specifically there’s no systematic deviation in the opposite direction during the years of rapid warming. As far as I can judge this means that the climate sensitivity of the model corresponds to the phase of rapid warming and is thus too high to explain the hiatus as the cooler phase of natural variability consistent with the model.
The link to graphics is erroneous in the above comment. It should be
http://pirila.fi/energy/kuvat/KosakaXieComp.png
I hope to write another post on what we can learn from simulations like that of Kosaka and Xie about climate sensitivity.