Posted on February 28th, 2014 in Isaac Held's Blog
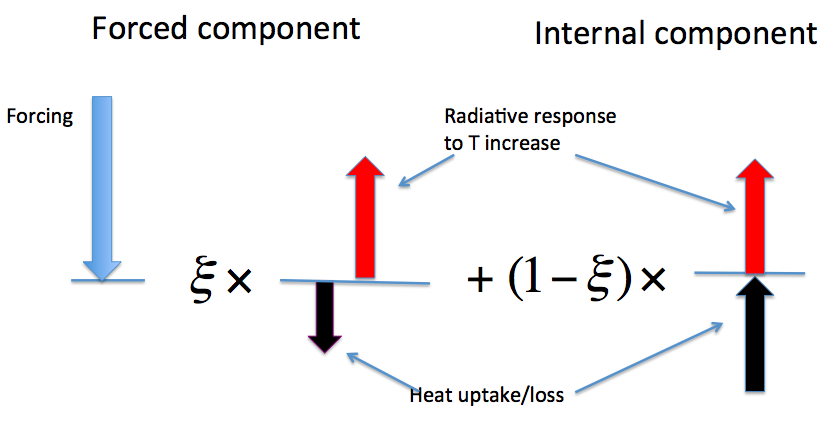 I’m returning to an argument discussed in post #16 regarding the decomposition of the global mean warming into a part that is forced and a part that is due to internal variability. I am not looking here for the optimal way of doing this decomposition. I am just interested in getting a better feeling for whether an increasing ocean heat content over time is a “smoking gun” for the forced component being dominant, a term Jim Hansen and others have used in this context. I’ll assume that we know that the heat flux has been into, not out of, the earth system (ie the oceans) averaged over the period in question, which could be the last half century or any period longer than a decade or two to insure that we can think in terms of a transient climate sensitivity (or transient climate response TCR) for the forced component. (AR5 WG1 Ch. 3 has a synthesis of the observations of ocean heat content). We’ll think in the most traditional terms, focusing on the global mean energy balance at the top of the atmosphere (TOA). Everything is considered to be a small perturbation from a control climate, and the assumption is that we can just linearly superpose the forced component of this perturbation and the component due to internal variability.
I’m returning to an argument discussed in post #16 regarding the decomposition of the global mean warming into a part that is forced and a part that is due to internal variability. I am not looking here for the optimal way of doing this decomposition. I am just interested in getting a better feeling for whether an increasing ocean heat content over time is a “smoking gun” for the forced component being dominant, a term Jim Hansen and others have used in this context. I’ll assume that we know that the heat flux has been into, not out of, the earth system (ie the oceans) averaged over the period in question, which could be the last half century or any period longer than a decade or two to insure that we can think in terms of a transient climate sensitivity (or transient climate response TCR) for the forced component. (AR5 WG1 Ch. 3 has a synthesis of the observations of ocean heat content). We’ll think in the most traditional terms, focusing on the global mean energy balance at the top of the atmosphere (TOA). Everything is considered to be a small perturbation from a control climate, and the assumption is that we can just linearly superpose the forced component of this perturbation and the component due to internal variability.
For the forced component, there is a 3-way balance between forcing , heat uptake
, and the radiative restoring proportional to the temperature response,
, with strength
inversely proportional to the climate sensitivity
. Here and in what follows,
is the change in forcing over the interval considered, so
is the usual sensitivity scaled by
When I refer to TCR in the following, it is also normalized in the same way. So TCR is simply the forced response in global mean temperature
.
is positive into the ocean. For starters, I’ll ignore the question of the efficacy of oceanic heat uptake.
The key assumption is that the relation between global mean temperature and the energy balance of the earth is the same for both the forced and internal components. So an internally generated perturbation in the global mean temperature is accompanied by an increase in the net outward flux at the TOA of
.
Set and similarly for the heat uptake
. We can write the heat uptake in the forced response in terms of the equilibrium sensitivity and the
:
So, adding the forced and internal components for the heat uptake:
It is the full that enters here. The heat flux is into the ocean if the equilibrium response is larger than the observed temperature perturbation.
This expression is transparent to the relative magnitude of the forced and free parts of . For this purpose, as in post #16, we can rewrite
so that
is the fraction of the temperature anomaly that is forced. And we get
One can write this in different ways (the way I chose in #16 being particularly obscure). We can just leave it is this form, from which we see that if the heat flux is into the ocean we must have (given all of our assumptions);
This all seems reasonable, but now let’s go back and re-examine our key assumption that an internal variation in temperature perturbs the TOA budget by an amount
, with the same value of
that occurs in the forced response. Why should it be the same constant of proportionality, especially if the internal variability has a different spatial structure than the forced response. So how do we relate the strength of this “restoring force” for internal variability to its strength for the forced response? Before getting back to this, we need to reintroduce the notions of efficacy of heat uptake.
For the forced response, when we try to emulate the behavior of GCMs, we find that we need to replace the expression with
The efficacy of heat uptake is defined as and is almost always larger than one when emulating GCMs – see Post #5 and Winton et al (2010). This is because the response to heat uptake is typically more polar amplified than the equilibrated response to the forcing, and perturbations at higher latitudes are restored less strongly by radiation to space than those at lower latitudes. So you get more bang for your buck by forcing at high latitudes. (Different parts of the forcing can have different efficacies as well, which is the sense in which this term was first used in this context, but I’ll ignore that here.) For a recent example of papers on this, see Rose et al 2014 which looks at the response in some aqua-planet atmospheric models to ocean heat uptake at different latitudes. Like most issues related to radiative responses, clouds feedbacks play an important role and are a major source of uncertainty in
.
Just as for the forced heat uptake, it is natural to expect the radiative restoring of low frequency internal variability to be weaker than that relevant for the equilibrium forced response. Both the forced heat uptake and the low frequency variability involve coupling to deeper ocean layers and this coupling is strongest in subpolar regions. So could it be the case that the restoring for low frequency variability resembles ? It might be interesting to see where the assumption
leads. Setting,
, we have
and
So we still have the result that positive heat uptake implies an equilibrium response over the time period in question (ie a temperature change over this period computed by assuming no heat uptake) that is larger than the actual temperature change. Expressing this in terms of the transient response we once again get the result that to be consistent with positive heat uptake we need . When efficacy is not equal to one, the assumption that
saves these intuitive and simple expressions.
Does hold in GCMs? How does the strength of the radiative restoring resulting from low frequency internal variability relate to that in the model’s response to heat uptake in the forced response? The smaller
the weaker the constraint on
. There is no reason to expect close agreement; there are undoubtedly different parts of the internal variability — focused on Northern compared to Southern subpolar latitudes, for example — that could be damped differently. But it would be interesting if
was at least correlated with
across models. I am not aware of any papers that have looked at this.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Quite a bit to take in here. Hopefully I’ve followed your point reasonably accurately and the following is relevant:
I’ve recently started looking at correlations in CMIP5 models between SAT and TOA energy flux/Ocean heat content during periods of variability. Specifically I constructed time series of 20-year trends for every member of a particular model’s ensemble, using the RCP45 scenario data, and defined variability in terms of difference from the ensemble mean/median. Note for ocean heat content I used zostoga – global average thermosteric sea level – for ease of access. I understand this should be pretty much the same thing because the ocean mass change is small in these model runs.
The first model I’ve looked at is HadGEM2-ES, mostly because its high sensitivity provides a kind of benchmark. I found no correlation between surface-air temperature variability and TOA flux trends, but there was a small positive correlation (weak, r-squared=0.22) between surface-air temperature variability and thermosteric sea level/ocean heat content trends. That is, ocean heat content trends are slightly amplified during periods of greater warming due to internal variability (and damped during slower warming periods) in this model, yet TOA flux doesn’t reflect this. Trying to figure out how to pick that apart…
I’ve also briefly looked at CCSM4 output. Need to recheck but preliminary results indicate a negative correlation between SAT variability and TOA flux trends. Haven’t checked zostoga data yet.