NOAA GFDL - Geophysical Fluid Dynamics LaboratoryGFDL - Geophysical Fluid Dynamics Laboratory

50. Volcanoes and the Transient Climate Response – Part II

Posted on September 3rd, 2014 in Isaac Held's Blog

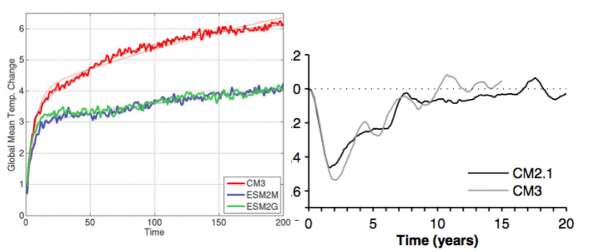Left:  The response to instantaneous quadrupling of CO2 in three GFDL models, from Winton et al, 2013a. Right:  The ensemble mean response of global mean surface air temperature to Pinatubo in two GFDL climate models, from Merlis et al 2014.

This is a continuation of post #49 on constraining the transient climate response (TCR) using the cooling resulting from a volcanic eruption, specifically Pinatubo.  In order to make this connection, you need some kind of model that relates the volcanic response to the longer time scale response to an increase in CO2. Our global climate models provide the logical framework for studying this connection.  Using simple energy balance or linear response models to emulate the GCM behavior helps us understand what the models are saying.  The previous post focused on one particular model, GFDL’s CM2.1.   The figure on the right (from Merlis et al 2014 once again)  compares the response to Pinatubo in CM2.1 with that in CM3, another of our models.  The CM2 curve is an average over an ensemble of 20 realizations with different initial conditions; the CM3 curve is an average over 10 realizations.  These two models have essentially the same ocean components but their atmospheric components differ in numerous ways.  Most importantly for the present discussion, the different treatments of sub-grid moist convection result in CM3 being a more sensitive model to CO2 increase, whether measured by the TCR or the equilibrium response.  One sees this difference in sensitivity in the left panel, showing the response to instantaneous quadrupling in three models, one of which is CM3.  One of the others, ESM2M, is very closely similar to CM2.1 (it also has the option of simulating an interactive carbon cycle, driven by emissions rather than specified concentrations of CO2, so is referred to as an Earth System Model.) ESM2G has the identical atmospheric component as ESM2M but a different ocean model.   As discussed in Winton et al 2013a, the different ocean models have little effect on this particular metric.  The analogous simulation with CM2.1 would be very close to the green and blue curves in the left panel.   Evidently the temperature responses to Pinatubo are not providing any clear indication that CM3 is the more sensitive model.

What is clear from the left panel is that the large difference between CM3 and the CM2-based models begins to build up between 10 and 50 years after the increase in CO2. The two models are close to each other during the initial (<10 year) fast response.  Presumably this is why the fast response to the volcanic forcing is similar in the two models.  (There is also a slower component to the volcanic response, but as discussed in #49 this is too small to see in the presence of the model’s noisy temperatures but is clearly seen in ocean heat content or sea level — Stenchikov et al, 2009.)  Comparing the time integral of the temperature response over times less than 10 years or so with the integrated volcanic forcing provides a modest underestimate of the TCR in CM2.1, as discussed in #49; in CM3 this underestimate is much more substantial.

Winton et al 2013a provide a three time-scale fit to CM3’s response to instantaneous quadrupling of CO2 (their Table 5).  Dividing by 2 to convert to doubling of CO2, the result is

T(t) = \mathcal{F}_{2X}\sum\limits_{i=1}^{3}\alpha_i[1-\exp(-t/\tau_i)] \equiv \mathcal{F}_{2X} h(t)

with \mathcal{F}_{2X} [\alpha_1, \alpha_2, \alpha_3] = [1.5, 1.3, 1.8]K  and [\tau_1, \tau_2, \tau_3] = [3.3, 58, 1242] years, with \mathcal{F}_{2X} = 3.5 W/m2.  The response to a \delta-function spike in forcing is obtained by differentiating,  g(t) = dh(t)/dt,

g(t) = \sum\limits_{i=1}^{3}(\alpha_i/\tau_i) \exp(-t/\tau_i)

For an arbitrary time evolution of the forcing \mathcal{F}(t), you can then write the response as a sum over contributions from the forcing at each earlier time \xi < t,

T(t) = \int_0^t \mathcal{F}(\xi) g(t-\xi) d\xi

where the forcing is assumed to vanish for t < 0.  If you plug in a linearly increasing forcing reaching \mathcal{F}_{2X} at year 70, you get a transient response of about 2.0K.  You can get a feeling for how it might be difficult to infer TCR directly from the surface temperature response to a volcanic eruption by playing around with this expression.

The difference in the shapes of the response functions in CM2.1 and CM3 is important, putting aside the difference in sensitivity.  A much larger fraction of the response by year 100 is realized in the first 10 years in CM2.1 than in CM3.  These different shapes have implications for attribution and near term projection of the forced response. The plateau-ish character of CM2’s response is likely related to the behavior of the model’s Atlantic Meridional Overturning Circulation (AMOC).  AMOC weakens in response to increasing CO2 in almost all models but then typically recovers slowly as the system equilibrates.  Weaker AMOC results in colder North Atlantic and colder global mean (warming in the Southern Hemisphere is invariabily weaker than the cooling in the north).  Consistently, AMOC strengthens in the CM2.1 Pinatubo simulations (Stenchikov et al, 2009).  Winton et al 2013b examine a version of ESM2M  in which the ocean currents are fixed and compare the response to CO2 (1%/year) in this model with the standard model in which currents, including AMOC, are free to change.  The model with fixed currents warms more rapidly on these intermediate time scales.  In this picture the plateau is not due to the absence of oceanic adjustment on multi-decadal time scales but due to a cancellation between the effects of the AMOC weakening and a gradual warming and reduction of heat uptake efficiency that would occur with fixed AMOC, as one might expect from something like a diffusive model of heat uptake.

The curious point is that ESM2M and CM3 share the same ocean model. The two models show similar reductions in AMOC in response to a warming perturbation.  It is the atmospheres that are different between these two models.  One hypothesis  is that the different atmospheres respond differently to similar changes in AMOC, due to different cloud feedbacks perhaps,  resulting in different shapes to their response functions on multi-decadal time scales.  The importance of cloud feedacks for the response to full suppression of AMOC (generated by adding a lot of freshwater to the North Atlantic)  is analyzed in CM2.1 in Zhang et al, 2010, although the focus there is on the changes in tropical rainfall rather than global mean temperature.  If this picture is correct, it is interesting that modeling uncertainty in cloud feedback can result in uncertainty in the time evolution of global mean efficiency of heat uptake.

Once one moves beyond the two-time scale fit to three or more time scales a simple emulator with discrete time scales begins to lose its appeal, as compared to models that start from a picture of vertical diffusion or some other continuous process.  The latter would potentially have fewer disposable parameters.  In fact, some colleagues have questioned why I haven’t started from a diffusive picture in these posts. It doesn’t bring us much closer to the underlying physics (ie the vertical diffusivity that one ends up using to emulate GCMs on this 100 year time scale has no simple physical interpretation) but if one has to rely on the response to AMOC to suppress the response on multi-decadal time scales to justify a model with well-separated fast and slow responses, then a diffusive starting point might be more parsimonious.  Ill try to return to this topic in a future post.

I realize that a theoretical discussion like this, in which I haven’t confronted the model with data on the response to Pinatubo, strikes some readers as unbalanced.  But I think we need a theoretical framework to think about how the volcanic responses and TCR are related, from which vantage point we can then think about the implications for TCR estimates of any discrepancies between modeled and observed volcanic responses.

(Thanks to several colleagues, especially Mike Winton, Tim Merlis, and Rong Zhang, for discussions on this topic.)

[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]

13 thoughts on “50. Volcanoes and the Transient Climate Response – Part II”

  1. The CM3 response to Pinatubo looks like it has a slightly damped oscillation with a period of about 3 years. (Looks like “ringing” after a perturbation). Since the curve is the average of many runs, it seems unlikely this arises strictly by chance. Is there anything in the model which could cause overshoot/undershoot type oscillation following a relatively short perturbation?

    1. We’ve noticed that as well. The most likely source for ringing on this time scale is presumably ENSO-like equatorial Pacific dynamics.

  2. A couple of points/questions

    1) I was pleased to see your comments on when the warming occurs in models with different sensitivities because I had recently started to wonder about this. Are there any publications that have looked at this more genrally in models to say whether the more sensitive models show greater warming in the slower responses. One possible explanation to me seems that the fast responses, such as WV,are based on ‘simpler’ processes that are shared among all models while the slower processes are based more on dynamical changes that develop in very different ways in different models.

    2) I was also interested in your AMOC observations. It appears, i) in these modelled climates, ii) in response to these forcings, iii) on timescale relevant to TCR, that AMOC is behaving as a negative feedback. Does it make sense to describe AMOC as a possible negative feedback?

    1. 1) I would like to think that this is the case, but at least in Winton et al 2010 (Table 2) the coefficients of variation for TCR and equilibrium sensitivity (TEQ) are similar. See also Dufresne and Bony 2008. This is harder to check in AR5 (Chap 9 Fig. 9.42) because the “TEQ” compared to the TCR is “effective sensitivity”, which does not give you the full spread of TEQ. Estimates of the TEQ of GCMs are often indirect because few are integrated long enough to allow an accurate direct estimate. I am sure that there are other more recent papers on this.

      2) There are attempts to include AMOC in simple emulators, but they usually have to use the AMOC simulated by a particular model as input as I understand it. I guess the problem with thinking of AMOC as a simple feedback is that its strength is not just a function of temperature in models. In particular, in these instantaneous CO2 increase simulations, or if CO2 increases 1%/year to doubling and is then held fixed, AMOC typically restrengthens as the system approaches its new warmer equilibrium. (But on second thought this is not that different from thinking of heat uptake as a feedback in the initial transient stage, with a strength that we call the heat uptake efficiency, as this makes no sense when the heat uptake goes to zero in the new equilibrium.)

  3. Thank you for a very interesting post. I have a few questions, if I may.

    You say that the AMOC strengthens in the CM2.1 Pinatubo simulations, and refer to Stenchikov et al 2009, which used the ECHAM4 model. I must have missed the discussion of the AMOC point in Stenchikov et al, but is there observational evidence showing that the AMOC strengthened over the Pinatubo episode? It doesn’t seem evident from the annual EM data in Fig. 7.1 of Muller et al (2014): A twentieth‑century reanalysis forced ocean model to reconstruct the North Atlantic climate variation during the 1920s (Clim Dyn), although that is from a model data-assimilation analysis.

    Also, do you think that this mechanism is the main explanation for why the effect, on an integrated basis, on GMST of global volcanic radiative forcing seems to be substantially less than for ERFs from GHG and most other forcings? Several studies have found a scaling factor of about 0.6 to be appropriate; using AR5 forcing time series (which convert AOD to RF using a slightly higher than usual factor of 25x) I find 0.5 or 0.55 works best.

    Your suggestion that the slow response (plateau with a small slope) in the AOGCM response functions is due to a cancellation between the effects of AMOC weakening and reduction of ocean heat uptake ‘efficiency’ (meaning kappa, I presume) is interesting. The Gregory plot slopes in Fig.2 of Winton et al (2013) become shallower after 50-100 years for both CM2.1 and CM3 – is that due to the AMOC weakening? A decline in ocean heat uptake efficiency wouldn’t in itself alter the slope of a Gregory plot, I think.

    It is a pity that CMIP5 abrupt 4xCO2 simulations are generally only 150 years long, too short accurately to estimate ECS for models that have very slow responses, like the GFDL ones.

    I note from Winton et al (2013) Fig.7 that all the GFDL models simulate, in their historical/RCP4.5 runs, a significant reduction in AMOC strength to have occurred by 2010. Don’t observations suggest this hasn’t happened (Fig. 7.1 of Muller et al 2014 and AR5 WG1 Fig 3.11.b)?

    The massive AMOC fall Muller shows in the early 1900s could perhaps explain why the first decade or two of the twentieth century were anomolously cold [which as Gillett et al 2012 noted biased up estimation of TCR based on twentieth century warming]?

    1. The Stenchikov et al 2009 paper that I linked to uses GFDL CM2.1. Perhaps you are thinking of a different paper? The response to Pinatubo is a stregtheing of AMOC of about 1 Sverdrup in this model. To see this small a change you need to average over a large ensemble of runs. You would not be able to see it distinctly in a single realization or in observations, going by the RAPID array results that you point to in AR5 WG1 Fig 3.11.

      It is obviously important to have reliable estimates of AMOC variations over the past century for attribution studies. Muller et al 2014 is a very interesting attempt, driving an ocean model with the 20th Century Atmospheric Reanalysis, which uses observations only of SSTs and surface pressure. The sharp increase in AMOC in the early 20th century in this result is striking. I need to look a this paper more carefully. There are a lot of things that can go wrong when running ocean models in this way — with strong restoring of surface temperature and no restoring of surface salinity, as the authors of this paper are well aware. See, for example, here.

      The pattern of heat uptake will change as the system evolves towards its new equilibrium, and the evolution in a “Gregory” plot of global mean temperature vs heat uptake will depart from linearity, even if AMOC does not change, to the extent that the changing pattern of heat uptake results in a different mix of atmospheric feedbacks. But changes in AMOC can also have an effect to the extent that they alter the pattern of heat uptake. So it is one of several factors that can move you off the linear trajectory in this plot. (Readers may want to refer to post #5.)

      1. I had mixed up the Stenchikov et al 2009 paper you referred to with the Stenchikov et al 1998 JGR paper Radiative forcing from the 1991 Mount Pinatubo volcanic eruption that I had already read; apologies. I have now read the correct, 2009, paper.

        I agree that ocean reanalyses should be treated with caution. In that connection, I was struck by how tiny a weight the ORAS4 reanalysis gives to observations relative to model predictions when updating its state.

        I of course accept that a decline in ocean heat uptake efficiency in conjunction with other factors can, as you say, move one off the linear trajectory in a Gregory plot. But it is interesting that for a large majority of CMIP5 models, a departure from approximately linearity – leaving aside the first few years – does not seem evident over the 150 years of the abrupt 4x CO2 experiment (e.g., in Andrews et al, 2012: Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere‐ocean climate models, GRL). CM2.1 and CM3 are exceptions, although they only exhibit nonlinearity after the first 100 years or so and such a late nonlinearity might not be obvious in a 150 year plot. The results in Williams et al (2008): Time Variation of Effective Climate Sensitivity in GCMs, J Clim. are also relevant. They found Gregory plot regressions to indicate that climate feedback was approximately constant for all the GCMs studied, indicating little time/state dependence on their centennial time scales.

    2. You refer to a “scaling factor” for volcanic forcing of 0.5 or 0.6 and I have seen that sort of thing referred to elsewhere but I have never understood what it means. As you can see in the figure in post #49, in CM2.1 if you compare the peak volcanic forcing (3 W/m2) and the peak temperature response (about 0.45K) and normalize to the 2X CO2 forcing in this model (3.5 W/m2) you get something like 0.525K which is only 35% of the model’s TCR. If you fit with a simple box model you get 1.1K, as discussed in the post. This is bigger because the temperature response (even the fast component of this response) is spread over a longer time period than the forcing. And it makes more sense since you get both a better integrated response and a good fit to the peak response. If you fit to the integrated temperature response up to year 10 to try to get all of the fast response you get closer (1.3K) to the TCR in CM2.1 (but you are still pretty far off in CM3) — although this is hard to do with a single realization. At least in CM2.1 (no claim that is true in all models) \beta, the strength of the radiative restoring in my notation, is quite similar between the CO2 and volcanic simulations — that is, you can’t justify a scaling factor on the basis of “efficacy” for this particular GCM. Maybe this GCM is an outlier in this respect, but if you have a reasonable simple emulator of this GCM there is no reason to use a scaling factor multiplying the radiative forcing (except to account for a small 10% or so difference between the response to positive and negative radiative forcing of the magnitude of the 2X response).

      1. I am trying to estimate TCR and ECS from real world data, not to emulate a model. Your point about some of the response to volcanic forcing not being captured because of its long timescale does not apply where, e.g., an energy budget model is used.

        Suppose mean changes deltaT in GMST, deltaF in global forcing and deltaQ in global heat uptake, all from preindustrial levels can be measured for any selected period, and the period chosen is 1990 to 2000. Ignore all non-volcanic forcing. The total integrated Pinatubo forcing will be captured by mean 1990-2000 forcing, as will the integrated surface temperature response over that period. Insofar as some of the forcing has cooled the ocean and full recovery has not occurred, there will be a loss of ocean heat content (OHC) recorded and hence a negative figure for mean heat uptake during 1990-2000. Leaving aside the possibility of non-unity ocean heat uptake efficacy, the full response (surface and OHC) to Pinatubo will have been recorded, just as to any other forcing occurring during the period.

        However, when this method is employed, it has been found in a number of studies that the estimate of effective sensitivity [deltaT/(deltaF – deltaQ)] is lower for volcanic forcing than for all other forcings (taken on an ERF basis). In practice only the aggregate of all forcings is reflected in GMST and OHC, and with an energy budget method changes are measured between a base period and an end period. The lower volcanic sensitivity is seen when switching between base or end periods with different levels of volcanic activity. It seems a fairly robust effect. But, on reflection, I don’t think the direct effect of volcanic strengthening of the AMOC – in terms of shifting heat from SH to the NH mid-latitudes, thereby reducing volcanic cooling where sensitivity is higher, is nearly enough to account for a scaling factor of ~0.6.

        1. Nic, thanks — I understand better what you are saying. The claim is that the efficacy of volcanic, or at least Pinatubo, forcing (in the terminology used by Hansen and others) is less than unity. In the notation I have used here, the value of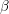 \beta needed to fit the volcanic response would be larger than what you need to fit the response to increasing CO2. As I have described, this is not the case in the CM2.1 GCM. It would be interesting to know if this model is an outlier in this regard.

          I think the limitations that we imposed on ourselves in Merlis et al, seeing if we could estimate TCR directly from the Pinatubo temperature response only (along with an estimate of the radiative forcing) without explicitly isolating the strength of the radiative restoring and heat uptake, seems unnatural to some, but sometimes it is useful to back away from the interpretation of the climate response and just think about the response itself. I’ll get back to using TOA fluxes and temperature responses together in another post eventually.

  4. Further to my first comment, I have realized that during 1880 to circa 1920, when Muller et al (2014) shows the AMOC as undergoing a huge decline and largely recovering from it, relative to the southern hemisphere the northern hemisphere warmed and then fell back (per HadCRUT4). Isn’t that the opposite of what it should have done according to theoretical understanding and model simulations? I am confused.

  5. We will have to accept that a decline in ocean heat uptake efficiency in conjunction with other factors can, as you say, move one off the linear trajectory in a Gregory plot. However, it is noteworthy that for a large majority of CMIP5 models, a departure from approximately linearity – leaving aside the first few years – does not seem apparent over the 150 years of the abrupt 4x CO2 experiment (e.g., in Andrews et al, 2012: Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere‐ocean climate models, GRL).

    There is a need to go further into the matter.

    1. Time dependence of heat uptake efficiency (heat uptake per unit global mean temperature perturbation) does not move one off the linear trajectory in the Gregory (T vs net radiative balance) plot. It just moves you along the line faster or slower. It is changes in the “efficacy of the heat uptake” (I realize that this is confusing) that has the effect of changing the radiative restoring strength by changing the spatial structure of the response, inducing a different mix of feedbacks, that accomplishes this. The Andrews et al paper focuses on the period of rapid growth in forcing; it is the difference between the period of rapid growth in forcing and stabilized forcing for which models suggest potentially large changes away from the constant slope model, complicating the relationship between the transient climate response and the equilibrium response.

Comments are closed.