Posted on March 9th, 2015 in Isaac Held's Blog
This animation is the response of a two-dimensional flow on the surface of a rotating sphere to a source that mimics stationary localized heating centered on the equator. The top panel is a north-south component of the wind — red is northward and blue southward. The bottom panel is the streamfunction of the flow –lines of constant streamfunction are the trajectories of fluid particles once the flow becomes steady. At the start of the animation the flow is purely zonal and the forcing is turned on instantaneously and then maintained. The loop covers about 40 days, but the pattern is fully set up in less than half that time. The continental outlines are just meant to help orient the viewer; the surface in this model is featureless. The setup is a classical one for generating a stationary Rossby wave propagating from the tropics into midlatitudes described by Brian Hoskins and colleagues in the late 1970’s and early 80’s (Hoskins et al 1977; Hoskins and Karoly 1981). This kind of wave is the essence of the teleconnections that atmospheric scientists talk about so frequently — patterns of flow that connect widely separated regions. Sometimes the correlations introduced into climate time series by these remotely forced responses can seem like spooky action-at-a-distance. But nothing could be further from the truth. They are just Rossby waves at heart.
The characteristic spatial scale of these stationary Rossby waves (not surprisingly known as the Rossby stationary wavelength) plays an important role in a lot of problems, not just in the response to tropical heating. About half a wavelength fits into the Continental US for example. So when the conditions are such as to favor anomalously poleward flow in the western half of the country, it is not unusual for there to be anomalously equatorward flow in the other half. There are no temperatures in this model, but you can imagine superposing this flow on an equator-to-pole temperature gradient with the equatorward and poleward flows advecting in cold and warm air.
(Is it advantageous for a political unit to control enough land to encompass at least half of a Rossby stationary wavelength, so that everyone is not hit simultaneously with the same kinds of weather extremes?)
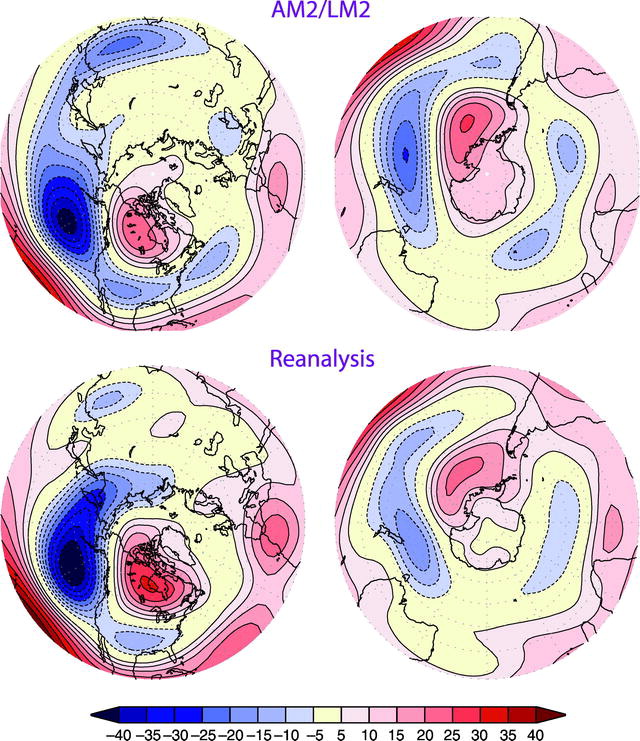
The role of teleconnections in the extratropical response to ENSO was clarified by the observational analysis of Horel and Wallace 1980 combined with the theoretical work of Hoskins and collaborators mentioned above– see Trenberth et al 1998 for a review. The figure below is an example of the simulation of these Rossby-wave ENSO teleconnections in an atmospheric GCM running over observed sea surface temperatures. These are polar projections of the regression of eddy geopotential at 200mb (the height of the 200mb pressure surface with the zonal mean removed) onto an ENSO sea surface temperature index — for Dec/Jan/Feb with the Northern Hemisphere on the left and the Southern on the right. Reds are highs (anticyclonic in NH) and blue lows (cyclonic in NH). The model is on the top and observations from reanalysis on the bottom. (This height of a pressure surface can also be thought of as proportional to the streamfunction.) Results are from the GFDL’s AM2.1 atmosphere/land model. The southern wavetrain gets less attention than its northern counterpart, but among other things plays a role in connecting trends in the Pacific to the pattern of temperature change around Antarctica.
There are some differences but there seem to be no fundamental mysteries here — no zeroth-order missing physics in the atmospheric model. Even freely running coupled models, if their ENSO variability is good enough, can generate teleconnection patterns with realistic amplitude and phase (see Fig. 19 in this paper on GFDL’s higher resolution CM2.5 model).
The animation at the top is a very idealized 2-dimensional model that is not meant to simulate the detailed pattern of response to any particular tropical heating, it is just meant to capture the essence of the underlying wave dynamics. To understand these responses you can use the geometric optics approximation which allows you to trace out the ray paths of the waves as they propagate through their inhomogeneous planetary-scale environment. To do this all you need is the local dispersion relation — the relation between the wave’s frequency and its wavenumber
for solutions that locally look like
. (
increases eastward and
northward.) The remarkable dispersion relation for these simplest 2D Rossby waves propagating on a background zonal flow
is
or
where is the speed with which the phase of the wave propagates eastward. Understanding
is the key to understanding Rossby waves, but let’s not worry about it for the moment and just assume that it is a positive constant. (It is vital that
is positive.) So the phase speed is always westward with respect to the zonal wind
on which the wave is propagating; stationary (
) Rossby waves can only exist if this zonal wind is positive. This is the typical situation in the troposphere, so stationary Rossby waves do exist. In the idealized model underlying the animation,
is set equal to (20m/s)
where
is the latitude. This is not particularly realistic, but among other things it avoids the question as to whether the wave can get out of the tropics, where
is weak in reality. The wavelength of the stationary wave,
, is
A distinctive property of this dispersion relation that colors much of meteorology is that waves longer than the stationary wavelength propagate to the west, the longer the wavelength the faster the westward propagation, while shorter waves propagate to the east with respect to the surface — but still to the west with respect to the flow that they are riding on. These shorter waves are the essence of the eastward propagating highs and lows we are all familiar with from midlatitude weather. They are more nonlinear than their larger wavelength stationary or westward propagating cousins, in part because they are destabilized by their interactions with the surface temperature field, and they roll up into vortices. One can think of the atmosphere as bathed in a spectrum of these waves of different scales, with a time average over more than a few weeks selecting out those wavelengths that are more or less stationary.
For those comfortable with the concept of group velocity, you can compute the -component of the group velocity by differentiating the dispersion relation with respect to
:
So the zonal group velocity is always eastward with respect to the phase speed and, in particular, stationary waves always have eastward group velocities — a striking property of Rossby waves. This explains why the propagation of the wavefront in the animation is eastward and why there is a large wavelike response over North America to the rearrangement of convection in the tropical Pacific associated with ENSO. If you compute the ray paths of the stationary waves emanating from the tropic for this special case in which (
is latitude) it turns out that they are great circles. All great circles passing through the source meet again at the antipodal point, which you can sort of see in the animation. This setup is nice pedagogically because of the simplicity of the ray paths. These ray paths can be more complicated in more realistic settings, but they often retain a great circle-ish aspect. (I have added a linear damping with 10 day e-folding so that the waves don’t have enough time to go into the other hemisphere and then return to the source and interfere with themselves –there is substantial dissipation in the atmosphere and, in any case, this kind of back and forth trajectory between the hemispheres is not relevant when the waves are propagating on more realistic zonal flows.)
So what is in the Rossby wave dispersion relation? It is the northward gradient of the radial component of the vorticity. In the special case of solid body rotation, you can show that the radial component of the vorticity is
, also known as the Coriolis parameter,
, which increases monotonically from the south pole to the north pole. (
is the rotation rate and
is latitude once again.) So the northward gradient,
, where
is the radius of the sphere, is positive everywhere. Plugging in some values for
you should get a Rossby stationary wavelength consistent with the results described above. If the flow is approximately in solid body rotation (remember that the surface of the Earth in an inertial reference frame is moving eastward at over 460 m/s at the equator) this northward vorticity gradient will be dominated by the contribution from the solid body rotation of the planet and the flow will support Rossby waves by a beautiful mechanism that I would like to return to in another post. In the meantime, here are some pictures to look at.
By the way, there are still a lot of open questions of climate relevance that one can begin addressing in this simple setting of two-dimensional flow on a sphere.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]