Posted on May 13th, 2015 in Isaac Held's Blog
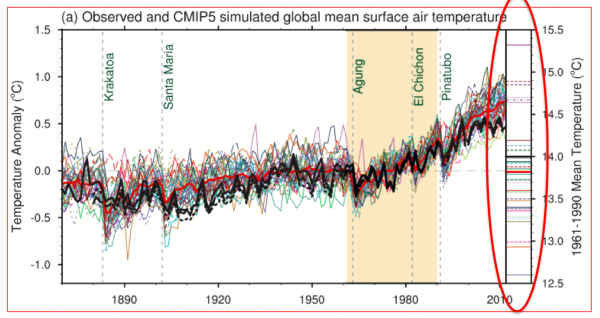
Fig. 9.8 from the AR5 Working Group 1 IPCC report. Global mean surface temperatures simulated by a set of climate models, shown as anomalies from the time mean over a reference period 1961-1990. Observations (HADCRUT4) in black; ensemble mean in red. On the right (circled) are the mean temperatures in the reference period.
Ch.9 of the AR5-WG1 report, “Evaluating Climate Models” is, in my opinion, the most difficult to write of any chapter in that report. You can think of hundreds if not thousands of interesting ways of comparing modern climate models to observations, but which of these is the most relevant for judging the quality of a projection for a particular aspect of climate change over the next century? This is an important research problem. Consider this figure, which shows the familiar simulated changes in global mean surface temperature over the past 150 years, in a set of models deposited in the CMIP5 archive, as anomalies from the model’s own temperature during some reference period (shaded). But the figure also shows in the narrow panel on the right side, circled in red, the models’ mean temperatures during that reference period. People tend to be disappointed when they see this — some models are better than others but the biases in the model’s global mean temperature are typically comparable to the 20th century warming and in some cases larger. If we are interested in projections of global mean warming over the coming century, or in the attribution of this past warming, should we trust these models at all, given these biases?
To start off, I would claim that it cannot be a valid requirement in general that the bias in some quantity needs to be small compared to the change that we are trying to predict or understand. Suppose we are interested in the forced response of global mean temperature to an increase of 10% or just 1% in CO2 rather than a 100% increase. Do biases in the models that we use for this purpose have to be 10 or 100 times smaller in order to trust their responses to these smaller perturbations? This makes no sense to me. I happen to think that these responses are quite linear over this range, in which case the size of the perturbation obviously has little relevance. But I am hard pressed to imagine any picture in which the bias in global mean temperature would have to be smaller than 0.01C to justify using a model to study global mean temperature responses. (The difficulty of studying very small responses in the presence of internally generated variability is a different issue entirely — if you were really interested in the response to such a small perturbation in a model for theoretical reasons, perhaps to test for linearity, you would have to generate a very large ensemble of simulations to average out the internal variability.)
On the other hand, consider sea ice extent. If your simulation is way off, it’s going to be hard to simulate the retreat of sea ice quantitatively — interactions between sea ice and the ocean circulation are likely seriously distorted due to the complexity of the ocean basin geometry. Plus, too extensive sea ice, say, would put it in regions of more incident solar flux, affecting the strength of albedo feedback. Sea ice issues are likely to be nonlinear in the sense that the mean state that you are perturbing matters a lot.
Why don’t models do better on the mean temperature? I think it is fair to say that all climate models have parameters in their cloud/convection schemes which which they tune their energy balance. This optimization step is necessary because cloud simulations simply are not good enough to get an energy balance to less than 1 W/m2 from first principles. Is it that some modeling groups are not very good at tuning their models?
One possibility is that there are tradeoffs between optimizing global mean temperature and some other aspect of the simulation. Imagine that a model has a bias in its pole-to-equator temperature gradient and that it is easier to adjust the models mean temperature up and down, with some parameter in the cloud scheme perhaps, than to correct this bias in the gradient. The result might be a choice between optimizing the global mean temperature and the sea ice extent. How would you weigh the importance of the bias in sea ice extent vs the bias in global mean temperature? I would probably give more weight to the ice because that is where the sensitivity to the mean state is likely to be stronger.
But this kind of explicit tradeoff is probably not the dominant reason for the bias in global mean temperature in most models. It is more likely that the models cloud schemes have been tuned to get a good temperature using relatively short runs of the model and then when one does longer multi-century integrations the model drifts — and it may be too expensive to iterate the model using these long integrations. So you live with the bias resulting from this slow drift.
Rather than the simulation of the climatology, why not use simulated trends in some quantity of interest as the metric with which to judge the credibility of model projections of that same quantity? If you are confident that the observed trend can be attributed to known forcings this is fine, but the familiar issue with uncertain aerosol forcing and uncertain contribution from internal variability makes this problematic for the global mean temperature, and the same issues arise for other quantities. The more credible and quantiative the attribution claim, the more valuable observed trends are for model evaluation.
Different views on the relative importance of different metrics are partly responsible for divergence between models. Are you better off with an optimized simulation of top-of-atmosphere spatial patterns of incoming and outgoing radiative fluxes, or of precipitation patterns? What if a proposed change in a model improves Amazon precipitation but causes African rainfall to deteriorate? If you are interested in how ENSO may evolves in the future under different emission scenarios, is it better to use a metric based on the quality of ENSO in simulations of the past century, or is it better to to use the same model to make seasonal forecasts of ENSO and use the skill of those forecasts as a metric? (Of course seasonal forecast skill is important in its own right — but its value as a metric compared to other possible metrics for a model of climate change is less self-evident.) If our models were close enough to nature, it would not matter which metric we used to push them even closer because all metrics would give a consistent picture. That different metrics agree or disagree on which of two versions of a model is better is itself a hint of how far one is from a fully satisfactory simulation.
Rather than defining metrics in a subjective way, basically guessing which metrics are most important, you can ask which metrics matter for a particular projection (ie of Sahel rainfall). If I sort models using some metric, some way of comparing the model to observations, does this also discriminate between model projections (i.e. between a dry Sahel in the future or a wet Sahel)? If so, and if I believe that this connection is physical, I can use it to sharpen my projection using that model ensemble. If there is no correlation between the metric and the projections, even if you were convinced that the metric was relevant, there would be no direct way of using it together with that ensemble of model results to improve the projection. This approach, sometimes referred to as looking for emergent constraints, strikes me as the most promising for the design of useful metrics. Returning to the figure at the top, should you use the value of a model’s mean bias to weight that model’s contribution, within a model ensemble, to future projections of global mean temperature? I don’t thinks so. The bias is not strongly correlated with the projected temperature change (see Fig. 9.42 here).
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]
Isaac, I would try to have the model match the actual surface temperature. Doesn’t a deviation cause problems with energy transfer to the ocean below the thermocline?
Fernando,
Any bias will cause some problems. Biases in surface temperature (and salinity) could create problems in the interaction between surface and deeper waters as you say, but I suspect that the most serious of these would be in higher latitudes where this coupling is strongest, so the global mean bias is probably not the best measure of the severity of those problems.
Thanks for the post,
I’m wondering how it impacts the interpretation of the spread of climate sensitivity as defined in the IPCC for instance.
This spread is implicitly considered as the change relative to a same reference temperature (e.g. the observed temperature). It permits a direct comparison between high/low sensitivity models. But a model’s ECS is calculated relatively to his own present temperature.
2 identical ECS does not necessarily suggest 2 identical warmer future climate since the values will be slaved to their present-day temperature. The model with coldest present-day climate is thus more sensitive to the warmest (independently of ECS). Do emergent constraints based on the spread of ECS (Fasullo and Trenberth 12; Sherwood al 14…) have to be interpreted differently?
Florent,
I am not sure that I understand your question. A model’s ECS is defined without reference to any observed temperatures as you say. But I don’t think it is true that the spread in sensitivity is implicitly considered in the IPCC reports as the change relative to some model-independent reference temperature. Future temperature projections by the models are always explicitly bias-corrected.
Thanks for your reply.
What I wrote could be misleading indeed.
I wanted to say that if, for instance, a model has a high ECS (4K) but a very cold present-day biais (2K), is it still a high sensitivity model?
Yes
Thank you for sharing your science !
I wonder if you would have any insight on the respective relevances to society of ECS and TCS ?
More specifically, it seems to me that we are façing now the effects of Transient Climate Sensitivity… while those of Equilibrium C.S. will not occur before a [rather unknown…] number of years ? (Related to the average depth at which… 90% to 93% of the excess heat will “sink” into the world ocean.)
If you scan through some of my previous posts on this blog you will find a lot on TCR. I would like to see more work on “emergent constraints” focusing on TCR.
Isaac, very interesting topic. I appreciate your blog a lot even though I don’t often comment.
Climate modelers have a massive advantage over those of us that don’t get to play with climate models and can only gain understanding through reading papers.
As an outsider it seems that models matching the past is a double-edged sword. Let’s say there are two models, model A that doesn’t get a great match of parameter X from 1900-2015 and model B that gets quite a good match.
On the one hand model B should be better at predicting the future of model X. On the other hand maybe model B’s target was parameter X (or at least included parameter X) from 1900-2015 and so is of maybe limited value in predicting the future of parameter X. (That is, no more than a curve fit to past data is expected to be a good fit to future data).
Some light was shed on the process for outsiders by Thorsten Mauritsen et al (2012). Thorsten suggested, in personal email correspondence, that modelers should become more transparent about the targets of the model development process.
I think this would help a lot. At least outsiders (and maybe it helps insiders as well) can have a better grasp of which parameters were focused on.
However, it doesn’t necessarily help in differentiating between our ideas about whether model A or model B will be better at predicting parameter X. It seems that this relies heavily on experience and cannot be an objective measure.
What do you think about these ideas?
The Mauritsen et al paper is an excellent example of striving for greater transparency. In one extreme, a theory or model can be a statistical fit for which everything rides on the procedure used to generate the model. In the other extreme, we may enjoy reading about how Einstein came up with general relativity, but that history is tangential to the science which rides on whether the resulting theory does or does not work. Climate models reside on the continuum between these two extremes — and where on the continuum they reside depends on which part of the model one is looking at!. I would like to push models towards the end of the spectrum in which they exist as hypothesis for how the climate system works without the need to know how they were created. It is not obvious how one does that, but I think part of it has to be to pull back from the high end simulations and put more effort into constructing a hierarchy of “elegant” models that one can analyze in depth and that are not thought of as becoming obsolete as new models are developed. See this essay.
I thing you do have to try to be objective when deciding which model provides better information about the future of X. The “emergent constraint” approach is one attempt to do that, trying to improve the way that we use the model ensembles that we have at hand.
Would I be right to assert that the model mean t anomaly is more often above the observations than below?
If you are talking about the model bias in the reference period, which is what the circled results refer to, this is not obvious from the plot. Of course, the difference between the model plume and the observations at present is what the “hiatus” discussion is all about. That’s a different issue from the focus of this post.
Isaac,
Interesting post. Based on what you know, is there any correlation between diagnosed CS and modeled Abolute temperature? I saw a plot of CS versus global mean temperature for the CMIP ensemble by Gavin Schmidt, where there did appear to be some correlation, but Gavin suggested the apparent correlation was due to the existence of closely related models contributing a large fraction of all the CMIP runs (eg, the various flavors of GISS models).
Since the vapor pressure of water increases exponentially with temperature (~7% increase per degree), a naive expectation would be for the models biased high in mean temperature to show more precipitation than models biased low in mean temperature. Do you know if there is in fact any correlation between global total precipitation and mean temperature bias?
Steve,
The plot that I referred to at the end of my post — Fig. 9.42 in Ch. 9 of WG1-AR5 — shows no correlation to speak of between climate sensitivity (which I believe is “effective” climate sensitivity) and bias in global mean temperature.
I haven’t seen a plot of global mean temperature and global mean precipitation in control simulations. There will likely be a nice correlation with total atmospheric water vapor, but global mean precipitation and water vapor are two different things, the former being constrained by the energy balance of the free troposphere above the boundary layer (see post #52). Since this energy balance is affected by both aerosols and clouds, I suspect that model differences in these would mess up any simple correlations with temperature that would otherwise exist.
Thanks for the post. You are technically correct to say that ECS in Fig. 9.42 is “effective” climate sensitivity, as it is based on regressing GMST change on TOA imbalance over only 150 years after an abrupt quadrupling of CO2. But that method arguably provides the best available estimate of actual equilibrium sensitivity for most models. The only models for which I’ve seen much evidence that it is badly biased are GFDL-ESM2-G and -M. Do you know why climate feedback strength goes on changing for longer in those two models than all others in the abrrupt4xCO2 simulations? They are, I think, unique in having very low TCR and 3+ K ECS values.
Nic, on the topic of this post, I doubt that it makes any difference whether you use effective or equilibrium climate sensitivity when looking for a relationship between a model’s mean temperature and its sensitivity. I’ll return to the important topic of transient climate response, equilibrium sensitivity, effective sensitivity, and efficacy of heat uptake in another post soon (I hope).
Thanks for the post. Ever since reading the IPCC AR5 chapter on assessing climate models I’ve been worried over the impact of tuning for known energy balance. Would be able to help me out and let me know if I’m way off base with my thinking here from my Comp Sci background?
It seems from most references I can find via the IPCC and papers like that by Mauritsen, it is pretty common practice when tuning climate models to adjust cloud parameters to balance TOA energy. It sounds like it is again pretty universal that this is a very necessary step to prevent unrealistic drift of TOA energy balance. Given that TOA energy balance drives everything in our climate, betting that right is pre-requisite to reasonable model behaviour. If I can call these observations step 1, please let me know if I seem accurate and correct in understanding things.
Step 2 then flows directly from the above. If we are tuning TOA energy through a variable like clouds and doing so as to reasonably match known observed values during the instrumental record, getting macros like surface temperature more or less correct shouldn’t be terribly surprising, no? Other than variations on the distribution of energy between oceans and atmosphere, if we are by design getting the increase/decrease in energy correct, the temperature deviations should be limited to distributing them perhaps a bit differently but on the whole matching shouldn’t be that far out?
question 3 would then be if models aren’t very nearly entirely omitting the process of predicting the central driving force of climate change in tuning TOA energy?
If I haven’t already run off the rails in the above, then my question immediately follows into questioning the predictive value of the climate models. TOA energy is the driver of climate change, and the models hand tune for it specifically to avoid drift to unrealistic results. What confidence can we have that heading into the future the models aren’t proceeding to drift into unrealistic TOA energy balances. After all, we can only tune for TOA energy in hindcasts, not forecasts. Worse, if we are specifically tuning for TOA energy, we really can’t evaluate the models accuracy of TOA energy because we hand balled that part heavily.
Needless to say, the overall view as I understand it of tuning models leaves me pretty shaky on their predictive value of the single most fundamentally important part of climate change in TOA energy. Would you be able to set me straight anywhere I’m getting things wrong or confused?
As a counterpoint to your line of argument suppose, hypothetically, that we have a model of the TOA infrared flux of the form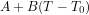
where 
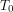is some reference temperature. For concreteness, think of this as a linearization of 
, where 
is some effective emissivity. Suppose we have a 5% error in 
, giving the same fractional error in 
and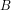 
after linearization. We get a 5% error in sensitivity, which is controlled by 
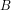, but if 
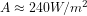the error in 
is 
or something like 6K if 
. This is oversimplistic but I think it captures the fact that you can make a large error in mean temperature while having a modest effect on sensitivity.
To be honest that’s a little bit over my head I’m afraid. I think I get the general idea your driving at though. The parameters being tuned are small compared to the overall energy flux in the system. When tuning something affecting cloud behaviour, clouds overall impact is − 17.1 Wm − 2 [Loeb et al. 2009], compared to the approximately 250Wm-2 combined affects from other processes adjustments to clouds are small. Am I understanding the heart of things there?
If so, I don’t see how that relates to my concern with assessing long term energy imbalance. With human forcings since 1750 sitting at 2.63 ± 0.26 Wm − 2 [Forster et al., 2007], a 5% change to clouds starts could dominate the energy balance. In the long term, climate modellers are correcting for the very important reason of getting reasonable results because otherwise drifting energy gives much worse results. I still feel troubled that models are tuning energy imbalance, in essence, by hand still. If I’m understanding that at all right, how can we evaluate the accuracy of model projections of TOA imbalance into the future?
This seems like a nice way to think about the issue. The question then becomes: to what extent does tuning of a model affect A and B by the same fractional amount when feedbacks are included?
As regards the figure from the IPCC report that motivates this post: An alternative for the second piece of information in this figure would have been to show a measure of climate drift in the different models (although this would not be a comparison with observations). Climate drift is small compared to the forced trends for global surface temperatures in most CMIP5 models, but I believe it is still ~20% in some cases.
Paul.
I would not argue that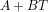
with the same fractional changes in A and B is a realistic starting point. More realistically perhaps, if we have instead 
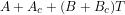, the same fractional error in 
and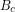 
, where the subscript refers to the cloud radiative effect say, this would give a much smaller change in total flux for a significant change in sensitivity as long as 
. For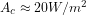
a 10% fractional error would give a big change in sensitivity for 2 W/m2 or maybe 1K error in global mean temperature. But I don't think that the total cloud effect and the cloud feedback are strongly correlated across model ensembles either ,but this is always worth looking into again. i was just trying to say that it does not follow automatically that a substantial error in total flux or global temperature implies that the model cannot tell us something about sensitivity.
Upto what level does tuning of a model affect A and B?
In my experience when you put a new model together from scratch without any regard to the energy balance you can easily be up to 5 w/m2 out of balance. Compared to the 240 w/m2 absorbed solar and outgoing infrared, that’s about a 2% error. If the fractional error in A and B were of this magnitude, this would be trivial error in B and in sensitivity. If your value of B is about 2 w/m2-K then running the model out to equilibrium the error in mean temperature would be 5/2 =2.5K. But this is just meant to be a counterexample to the common argument that an error of this magnitude in the energy balance automatically means that you cannot model climate sensitivity at all. I am not saying that fractional errors in A and B are actually comparable.