Posted on April 16th, 2011 in Isaac Held's Blog
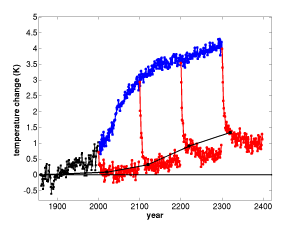 Evolution of global mean near-surface air temperature in GFDL’s CM2.1 climate model in simulations designed to separate the fast and slow components of the climate response in simulations of future climate change, as described in Held et al, 2010.
Evolution of global mean near-surface air temperature in GFDL’s CM2.1 climate model in simulations designed to separate the fast and slow components of the climate response in simulations of future climate change, as described in Held et al, 2010.
Continuing our discussion of transient climate responses, I want to introduce a simple way of probing the relative importance of fast and slow responses in a climate model, by defining the recalcitrant component of global warming, effectively the surface manifestation of changes in the state of the deep ocean.
The black curve in this figure is the evolution of global mean surface air temperature in a simulation of the 1860-2000 period produced by our CM2.1 model, forced primarily by changing the well-mixed greenhouse gases, aerosols, and volcanoes. Everything is an anomaly from a control simulation. (This model does not predict the CO2 or aerosol concentrations from emissions, but simply prescribes these concentrations as a function of time.) The blue curve picks up from this run, using the SRES A1B scenario for the forcing agents until 2100 and then holds these fixed after 2100. In particular, CO2 is assumed to approximately double over the 21st century, and the concentration reached at 2100 (about 720ppm) is held fixed thereafter. The red curves are the result of abruptly returning to pre-industrial (1860) forcing at different times (2000, 2100, 2200, 2300) and then integrating for 100 years. The thin black line connects the temperatures from these four runs averaged over years 10-30 after the abrupt turn-off of the radiative forcing.
One can think of the red lines as simulations of what we might call instantaneous perfect geoengineering, in which one somehow contrives to return the CO2 (and all of the other forcing agents in these simulations) to pre-industrial values. Perfect geoengineering so defined must be clearly distinguished from two other simple hypothetical scenarios discussed in the literature. (Let’s simplify things by just thinking of CO2 as the only relevant forcing agent.) One such scenario consists of just holding the CO2 fixed after a certain time, as in the A1B scenario after 2100 (the blue line) in the figure. The warming that occurs after 2100 as the system approaches its final equilibrium is referred to as the “committed warming” but it might be better to refer to it as the fixed concentration commitment. A second, in many ways more interesting, simple scenario (e.g. Solomon et al, 2009; Matthews and Weaver, 2110) consists of abruptly setting the emissions to zero. This is another definition of commitment, which we might call the past emissions commitment, the study of which requires a coupled carbon-climate model. Unlike the fixed concentration commitment, it often results in temperatures that stay roughly unchanged for centuries — the warming due to the reduction in ocean heat uptake is roughly balanced by the ocean uptake of CO2. Perfect geoengineering is much harder than even setting emissions to zero, of course, since one would have to take enough CO2 out of the atmosphere to return to its pre-industrial value. Needless to say, we are not interested in this scenario because of its practical relevance but rather as a convenient probe of climate models.
There are similarities in the evolution after the turnoff of the radiative forcing for the 2100, 2200, and 2300 cases (these all have the same radiative forcing before the turn-off). At first the temperature decays exponentially, with an e-folding time of 3-4 years. An exponential fit yields a cooling in this fast phase of 2.6-2.7K in each case, leaving behind what we refer to as the recalcitrant warming. The spatial structure of the fast response is very similar in these three cases as well, and differs substantially from the spatial structure of the recalcitrant remnant. These are single realizations so some of the slow evolution after the turnoff of radiative forcing could be due to background internal variability. See Held et al (2010) for some further discussion of these simulations. Wu et al (2010) discuss aspects of the response of the hydrological cycle in similar model setups.
In thinking about the recalcitrant warming, it is useful to return once again to our two box model (post #4, ignoring the limitations of this model discussed in post #5)
On time scales long compared to the fast relaxation time of the surface box with temperature , we have
.
When the forcing is turned off, The solution relaxes on the fast time scale to
,
so the response is the sum of the recalcitrant part and fast response proportional to the forcing
An important implication of this plot, taking it at face value, is that the recalcitrant component of surface warming is small at present, implying that the response up to this point can be accurately approximated by the fast component of the response in isolation, which simply consists of rescaling the TCR with the forcing.
Another implication is that acceleration of the warming from the 20th to the 21st century is not primarily due to saturation of the heat uptake (this only accounts for the 0.4K growth of the recalcitrant component), but is primarily just due to acceleration of the growth of the radiative forcing.
It is important to keep in mind the limitations of this idealized picture. There is no reason to expect the slow response to be characterized by one time scale. But more importantly for this line of argument, there is no obvious reason why intermediate time scales, related to sea ice or the relatively shallow circulations that maintain the structure of the main thermocline, could not play more of a role in the transient response of surface temperature, filling in the spectral gap between our fast and slow time scales, and requiring a more elaborate analysis of the linear response in the frequency domain.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac – Your simulation assumes a CO2 concentration that remains fixed after reaching 720 ppm. If the concentration rose until a higher level was reached – e.g., 1000 ppm – do you have any idea what the recalcitrant component would be at 2100 or what its ultimate temperature contribution might become? Over the long haul, is CO2 the only GHG we need consider or will there be other long-lived contributions that make total CO2 equivalents exceed the CO2 component alone in driving up the recalcitrant fraction? As fossil fuel combustion subsides, what will be the effect of reductions in negative aerosol forcing?
At this level of description of the model behavior, you can just think of the global mean radiative forcing as the input, whatever the contribution of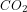 versus other greenhouse gases or aerosols. If
versus other greenhouse gases or aerosols. If 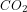 increased to something higher (or lower) than 700 by the end of the century, I think the recalcitrant fraction in 2100 would be about the same — the fast and the slow (recalcitrant) components in this GCM would both roughly scale with the forcing. If the stabilization occurs later, the recalcitrant fraction will be greater at the time of stabilization.
increased to something higher (or lower) than 700 by the end of the century, I think the recalcitrant fraction in 2100 would be about the same — the fast and the slow (recalcitrant) components in this GCM would both roughly scale with the forcing. If the stabilization occurs later, the recalcitrant fraction will be greater at the time of stabilization.
I hope you don’t mind questions from somebody on a steep learning curve.
1) If i rewrote one of the sentances in the first paragraph by adding two words would it still make sense or am I mis-understanding something? Here goes
“….by defining the recalcitrant component of global warming, effectively the *future* surface manifestation of *present* changes in the state of the deep ocean.”
2) Is the recalcitrant component of global warming simply a movement of energy through the system? Is energy being lost to the deep ocean only to resurface at a later date to add to the surface temperature? Or is it something more complex in how the system has been altered such as changes in ocean currents? I’m just wondering if it is Trenberth’s ‘missing heat’ (hopefully that isn’t too crude).
3) If you left the red line for the turn off at 2100 to run to 2300 would it have the same slope as the blue line, i.e. is the continued warming in the blue line just a manifestation of the recalcitrant component?
Thanks
With regard to 3) I just noticed the black line seems to have the same slope as the blue line, is that just co-incidence or bad eyeballing?
Your understanding seems fine to me. Your inserts in (1) are fine; (2) I think it is primarily just energy being sequestered but changes in circulation can certainly complicate matters; with regard to the “missing heat”, that is more a question of whether some is sequestered deeper than the layers typically studied in ocean heat content data sets, (3) to the extent that the fast component is proportional to the forcing, the growth of the “committed” warming — the blue line after 2100 — should be the same as the growth of the recalcitrant component as defined by the black line.
It seems that at least some of the processes that deliver energy to the deep ocean may have undergone multidecadal trends over part of the 20th century.
e.g. https://web.archive.org/web/20120916163520/http://ic.ucsc.edu/~ammoore/ocea290e/mcphaden+zhang_nature_2002.pdf
For example if the PDO has contributed to a trend in overturning for 60-70 years of the 20th century then that would have possible implications for the magnitude of TCR. It looks to me that for at least this part of the 20th century that TCR may have undergone a trend. You seem to describe TCR as a fairly fixed value (e.g. 1.5oC for a doubling of CO2). But it could be possible that this component itself has trended over much of the 20th century. Based on the above paper the implication would be that TCR could have risen over the period with the transition from general La Nina conditions to general El Nino conditions around the mid-1970’s. I guess the variation may be small enough to have little implication on how much energy at any on time is partitioned into the TCR or recalcitrant part of the climate response but it seems like something that should be considered.
Do you consider TCR as a constant over time? Do you consider overturning as a possible source of long term variation in TCR that goes beyond just short term noise? It also seems to have possible implications for attribution of warming over different periods of the 20th century. For example in part the accelerated warming from the 1970’s onwards could be due to an increase in TCR as overturning slows, less energy is transported to depth and more remains at the surface. It seems to suggest that internal variability (of the oceans) be treated as a sort of forcing on the surface, especially with respect to the TCR component.
OK I found this article by Toggweiler which sets out the issues in a clear way.
I notice you get an acknowledgement on it. I’m still curious of the potential impact this issue might have on the TCR.
Like HR, I am wondering about the possible relation to the “missing heat”. The recalcitrant component would depend on how fast energy is transferred down to the deep ocean. That transfer would presumable be analogous to the “gamma” constant of the slab model. People seem to think that it is hard to estimate the size of this transport directly, but are there ways to constrain it? (sea level measurements, surface temperature change etc?)
Isaac,
I’m a little confused and want to make sure I’m understanding this post correctly. Does the recalcitrant warming indicate that under a certain forcing there will be multiple equilibrium climate states with different spatial patterns, and some of them have higher global mean temperature than others?
Thanks
Zhaoyi,
No, there is no implication for multiple equilibrium — just fast and slow responses with different spatial patterns. If you focused only for the fast time scale, I guess you could say that by perturbing the system with the pattern of the slow response, the perturbation would hang around for a while, decaying slowly –so in that sense you could say that there was kind of a “multiple equilibrium” viewed from the fast time scale, but this would be a confusing terminology.