Posted on April 5th, 2011 in Isaac Held's Blog
Upper panel: Interdecadal component of annual mean temperature changes relative to 1890–1909. Lower panel: Area-mean (22.5°S to 67.5°N) temperature change (black) and its interdecadal component (red). Based on the methodology in Schneider and Held, 2001 and HadCRUT3v temperatures. More info about the figure.
Perhaps the first thing one notices when exposed to discussions of climate change is how much emphasis is placed on a single time series, the globally averaged surface temperature. This is more the case in popular and semi-popular discussions than in the scientific literature itself, but even in the latter it still plays a significant role. Why such an emphasis on the global mean?
Two of the most common explanations involve 1) the connection between the global mean surface temperature and the energy balance of the Earth, and 2) the reduction in noise that results from global averaging. I’ll consider each of these rationales in turn.
The energy balance of any sub-portion of the atmosphere-ocean system is complicated by the need to consider energy fluxes between this selected portion and the rest of the system. It is only for the global mean that the balance simplifies to one involving only radiative fluxes escaping to space, providing a basic starting point for a lot of considerations. But is there a tight relationship between the global mean surface temperature and the global mean energy budget?
I have already indicated in a previous post (#5) that this coupling is not very tight in many climate models. In these models, the pattern of temperature change in response to an increase in CO2 evolves in time, becoming more polar amplified as equilibrium is approached. And, as a consequence of these changes in spatial pattern, the relationship between the global mean temperature and global mean top-of-atmosphere (TOA) flux changes as well. Among other things, the dynamics governing the vertical structure of the atmosphere is very different in low and high latitudes, and one needs to know how the vertical structure responds to estimate how radiative fluxes respond. There are also plenty of reasons why cloud feedbacks might have a different flavor in high and low latitudes, and might be controlled more by changes in temperature gradients than in local temperature. The potential for some decoupling of global mean surface temperature and global mean TOA flux clearly seems to be there.
[One sometimes sees the claim that it is the 4th power in the Stefan-Boltzmann law that primarily decouples the global mean temperature from the global mean TOA flux. But this is a very weak effect, at most 5% according to my estimate; the effects of differing vertical atmospheric structures in high and low latitudes, and the effects of clouds, are potentially much larger.)
There is a tendency, especially when discussing “observational constraints” on climate sensitivity, to ignore this issue — assuming, say, that interannual variability is characterized by the same proportionality between global mean temperature and TOA fluxes as is the trend forced by the well-mixed greenhouse gases. This is not to say that the internanual constant of proportionality is irrelevant to constraining climate sensitivity. One can imagine, if interannual variability is characterized by one spatial pattern, and the response to CO2 by another pattern, that one might be able to compensate for this difference in pattern when trying to use this information to constrain the magnitude of the response to CO2.
Let’s turn now to the noise reduction rationale.
There is plenty of variability in the climate system due to underlying chaotic dynamics, in the absence of changing external forcing agents. To the extent that a substantial part of this internal variability is on smaller scales than the forced signal, spatial averaging will reduce the noise as compared to the signal. But is global averaging the optimal way to reduce noise?
Suppose one has a time series at each point on the Earth’s surface. There are a lot of different linear combinations of these individual time series that one could conceivably construct; the global mean is just one possibility. Some of these linear combinations will have the property of reducing the noise more than others. One can turn this around and ask which linear combination reduces the noise most effectively.
Tapio Schneider and I examined this question in a paper in 2001. One has to first define what one means by “minimizing noise”. In our case, we define a “signal” by time- filtering the local temperature data to retain variations on time scales of 10 or 15 years and longer and then define the “noise” to be what is left over. We are not saying that this signal is forced by exterrnal agents; it is presumably some combination of forced responses and free low-frequency variations. But the forced response due to slowly varying external agents is presumably captured within this signal. We then maximize the ratio of the variance in the “signal” to the variance of the “noise”. This is an example of discriminant analysis, in which you group the data and look for those patterns that best discriminate between the data in different groups. (Roughly speaking, the different decades are different groups for our analysis, although we do not actually use non-overlapping decadal groups.) The result is a ranked set of patterns and a time series associated with each pattern. The most dominant pattern, the one that reduces the noise most effectively, turns out to be quite different from uniform spatial weighting. The animation at the top of the blog shows the evolution of annual mean temperatures filtered to retain the 4 most discriminating patterns (this is the number of patterns with a ratio of signal to noise greater than one.) Tapio has comparable animations for the individual seasonal means.
A more popular approach to multivariate analysis of the surface temperature record, complimentary to discriminant analysis, is “fingerprinting”. Here models provide one or more patterns (starting with the pattern forced by the well-mixed greenhouse gases) and, using multiple regression, we test the hypothesis that these patterns are discernible in the observed record. These approaches are complimentary because discriminant analysis does not start with a given pattern and test the hypothesis that it is present in the data; it is just a way of describing the data. A purely descriptive analysis can only take you so far, but for some purposes it is advantageous to let the data tell you what the dominant patterns are, rather than having models suggest how to project out interesting degrees of freedom.
In any case, you can do better than take a global mean if you want to reduce the noise level in the data.
The information content in the global mean depends on how many distinct patterns are present. Let’s assume that one has already isolated from the full time series what one might call “climate change”, either through a discriminant analysis or some other algorithm. If the evolution of the signal is dominated by one perturbation pattern , and if we normalize the pattern
so that it has an integral over the sphere of one, we can just think of the perturbation to the global mean as equal to
, the amplitude of the pattern. If 2 (or more) things are going on that contribute to observed climate changes, you are obviously going to need 2 (or more) pieces of data to describe the observations, and the value of the global mean is more limited.
If the response to CO2 , or the sum of the well-mixed greenhouse gases, is linear, the spatial response of surface temperature could still be a function of the frequency of the forcing changes. If one assumes in addition that this frequency dependence is weak, as in the “intermediate” regime discussed in earlier posts, then one can expect evolution of the forced response that is approximately self-similar, with a fixed spatial structure, in which case the global mean is a perfectly fine measure of the amplitude of the forced response.
It is easy to come up with examples of how an exclusive emphasis on global mean temperature can be confusing. Suppose two different treatments of data-sparse regions such as the Arctic or the Southern Oceans yield different estimates of the global mean evolution but give the same results over data rich regions. And suppose, for the sake of this simple example only, that the actual climate change is self-similar, and is, in fact, entirely the response to increasing well-mixed greenhouse gases. One is tempted to conclude that the method that gives the larger global mean warming suggests a larger “climate sensitivity”. But both would be providing the same estimate of the response to greenhouse gases in data-rich regions.
There are other interesting model-independent multivariate approaches to describing the instrumental temperature record besides the discriminant analysis referred to above. Typically one needs to choose something to maximize or minimize. For example, in this paper, Tim Del Sole maximizes the integral time scale, , where
is the autocorrelation function of the time series associated with a particular pattern. I encourage readers to think about other alternatives.
Addendum 5/8/11:
In response to a question below, here (thanks to Tapio) is the spatial weight vector that is multiplied by the data to generate the canonical variate time series for the first (the most dominant) term in the discriminant decomposition of the annual mean data set shown at the top of the post. The lower panel shows the filtered and unfiltered canonical variate time series. The shading is the band within which 90% of the values should lie in the absence of interdecadal variability, as estimated by bootstrapping.
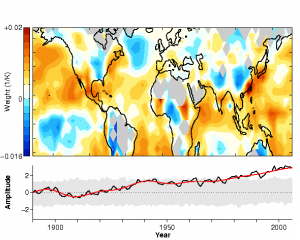
The low weights over land are interesting. Although this is only the first term in the expansion, it suggests that climate variations over land can be estimated by using a discriminant analysis of ocean data alone and then regressing the resulting canonical variates with the land data. This is consistent with dynamical model studies, such as Campo and Sardeshmukh, 2009, of the extent to which land variations are slaved to the ocean on these time scales.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Part of the utility in talking about a “global temperature anomaly”, at least in popular discussions, is that it is a relatively uniform field (within a factor of 2-3 or so [maybe a bit more near the poles]);what’s more, anomalies are often well-correlated even over synoptic-scale distances. It therefore provides some intuition as to what is happening. While a “global temperature increase of 3 C” may not mean much to a farmer in Wisconsin, if he applies that number to the temperature change averaged over Wisconsin, he is probably going to be more in the ballpark than if he applied that sort of reasoning to the precipitation anomaly field, whose “globally averaged value” is not often discussed in any useful setting.
In contrast, the paleo-climate community generally does not talk in such terms when discussing events such as the abrupt climate changes involved with see-saw like oscillations during the last glaciation, with anomalies anti-correlated between hemispheres. So the utility of a ‘global temperature anomaly’ as a variable depends on the nature of the forcing, but it’s reasonable (to first order) to think in such terms for increases in CO2. This utility probably breaks down as you continue to make your spatial scale smaller, but the science is, for better or worse, currently at a stage where the regional effects are details that branch off of the “big picture.”
Thanks for the post, I’ve got side-tracked by one question that your post raised which I hope isn’t too much off topic.
One idea I have come across revolves around the importance of the
homogeneoustruly global nature of the warming trend in recent decades. For example if one plays with the NASA-GISS mapping tool https://data.giss.nasa.gov/gistemp/maps/ the mid-20th century warming has regions of warming and cooling while the most recent warming period is almost globally warmer. It’s suggested this is important supporting evidence for attribution of the warming.At the height of the mid-20th century warming period your animation seems to have warming as a fairly complete global phenomenon which seems quite different to NASA-GISS. Is my observation about your work accurate? Is the pattern of warming using your methodology very different to others? Is it possible to think of the homogeneous/heterogeneous nature of the warming signal as being a methodological issue/artifact?
The discriminant analysis is a filter. This filter will make things more spatially homogeneous if and only if it is the more homogeneous components of variability that most clearly distinguish the inter-decadal from higher frequency variations. Is this process homogenizing the mid-century warming more than the late century warming? I guess I would need to quantify that before commenting further. It’s an interesting point.
It would be interesting to see the spatial distribution of the noise amplitude. Does it occur uniformly, or at temperate latitudes, or something else?
In discriminating between signal and noise, you have to have statistical models for each. Supposing we keep things linear for the moment, we can have a subspace over which the signal varies, and another subspace over which the noise varies, and observations over the sum of the two. (In the above example, the subspaces appear to be frequency bands above and below 1/10yrs.) The subspaces are probably not orthogonal in general (although your frequency bands are), so complete separation is unlikely. You would then get four components: a part attributable to the signal, a part attributable to the noise, a part attributable to both (so you couldn’t tell which was causing it) and a part attributable to neither (an indication of whether your statistical models are effective). The subspace intersection and null space intersection give the latter two.
A linear sum (signal+noise) of non-linear models should also be feasible, although there could be multiple solutions. The translates of each model manifold would act like a set of curvilinear coordinates. The coordinates of the observed history would give the signal, noise, and indeterminate components. (The indeterminates would be along curves of intersection of signal and noise manifolds.)
So you could, for example, take an ARMA(2,1) noise model, a ‘low frequency band’ signal, and determine how much was attributable to each, how much couldn’t be distinguished, and where (spatially) each component was strongest. By considering a range of different noise models and signal models, you could perhaps determine where to concentrate future measurements to be able to best distinguish between them or eliminate them, or how sensitive a result was to outlying observations in a small geographic area.
Perhaps the terminology “signal” and “noise” is a source of confusion (or perhaps I am confused). If you look at the temperature data from a random year, can you tell which decade it belongs to? Which aspects of the temperature field would you look at to optimize your chance of making the right assignment? Is looking at the global mean the surest way? These are the kind of question that the discriminant analysis tries to answer. An explicit noise model doesn’t seem necessary in this context. Asking different questions will motivate different ways of looking at the data, of course
Now I’m confused too. If you have the data for all the years as your training set, then it is trivial to construct a discriminator that identifies any given pattern. Consider each year’s data as an n-dimensional point, consider the decade as a function sampled on this set of of points, and interpolate. The question only becomes interesting when you restrict your interpolation function to some smaller subspace – like linear discriminants – so you have to find a best fit to the sample using functions of a given form. This restriction reflects your assumptions about the distribution of the data. For example, if you assume each class has Gaussian distributions with equal covariances but differing means, the linear discriminant is optimal. Without assuming equal covariances, a quadratic discriminant is optimal. And so on. The space of functions you use for ‘curve-fitting’ boundaries between classes depends on your implicit assumptions about the space of distributions that you use to model the data.
By choosing to minimize variance, for example, you implicitly optimize for a Gaussian distribution. That’s not unreasonable, of course – they’re very common. But I think it does count as a sort of noise model. I’m no expert, though, so I may have gotten confused over what you’re trying to do.
As you said – you have to define what you mean by “noise” and what you mean by “minimizing” it. (Minimum noise having maximum probability under some distribution.) Your way of dividing it up is very reasonable. But I thought that it could be generalized to other perhaps more realistic noise models, and assumed this sort of generalization was what you were asking for. No problem, though – it was just a thought.
I was both confused and misunderstood your comment. As you say, the whole point is to discriminate with a few degrees of freedom only. And to determine that one’s algorithm is optimal requires that one thinks of the observations as part of an ensemble. So in this sense there is an implicit (Gaussian stationary) noise model underlying our analysis. Thanks for the clarification. Needless to say, statistics is not one of my strengths.
Isaac. I enjoyed your post. There is another very different way to use discriminant analysis to describe the temperature record, and it has a connection to fingerprinting that might help clarify things.
Suppose you have two model runs, one forced and one unforced. If the forced response varies in time and can be idealized as additive and independent of unforced variability, then any component in the forced run should have larger variance than in the unforced run. In fact, the larger the ratio of the two variances, the larger the forced response. This reasoning suggests that the component with the largest possible ratio must be associated with the strongest response. Discriminant analysis can be used to find the weights that maximize the ratio of the forced to unforced variance. The resulting discriminant function must then be the thing to look at to best discriminate between forced and free fluctuations.
An interesting by-product of the forced-to-unforced discriminant pattern is that it optimizes detectability in the climate model. What I mean by this is that if you were to use this discriminant pattern as your forced pattern, and apply fingerprinting to the output of the forced run, then this pattern maximizes the statistic for testing climate detection.
When I used this approach to define the forced response pattern in a recent paper, I was surprised to find that discriminant analysis detects only one forced pattern, despite the fact that the forced runs are subject to multiple climate forcings. The time series of this pattern clearly shows that it captures both the warming trend and volcanic signals. I was not aware of your self-similarity argument as a possible explanation and would like to learn more about.
At first I was confused about how it is possible to attribute changes to specific forcings given that discriminant analysis identifies only one forced component. The answer is that all attribution studies that distinguish different forcings use more than surface spatial structure. Specifically, they use temporal information, vertical structure, or seasonality in the response pattern. It is easy to see how additional information, like temporal evolution, can enhance discrimination: for instance, the response to anthropogenic forcing is primarily a trend whereas the response to volcanic aerosols occur at very specific and isolated points in time, so even if the response is pattern is similar the time evolution is very different. The fact that discriminant analysis of annual mean surface fields identifies only one significant component implies that it is absolutely impossible to distinguish different forcings based on surface spatial information alone. I wonder if your self-similarity argument explains this empirical result.
Isaac: Thanks for the clear and insightful post. I have one comment regarding “optimal fingerprinting.” It is, as you write, complementary to space-time filtering of observations, which focuses on slow climate variations. But I do not think it is the optimal complement, for several reasons. Optimal fingerprinting relies on a linear regression of observations onto simulated climate change signals. The simulated climate change signals typically are linear trends (e.g., of surface temperature). To obtain a well-posed regression problem, it is furthermore necessary to reduce the effective number of degrees of freedom in the climate change signal, for example, by severe spatial smoothing. Climate change is then said to be detected if the generalized linear regression of observations onto the climate change signal is statistically significant, relative to a noise background of natural variability that is likewise estimated from a simulation. So at least three assumptions are typically made: (1) climate change “signals” evolve approximately linearly in time; (2) models simulate natural variability adequately; (3) signals of interest have very large spatial scales (typically thousands of kilometers). Assumption (1) seems unnecessary to me, (2) is best not made at the outset, and (3) may not always be adequate, for example, for some forms of aerosol forcing, which can give spatially localized responses.
I think it would be better to separate the analyses of simulations and observations to a greater degree. One could compute “slow manifolds” of simulations and observations separately (e.g., by a discriminant filter, or Tim DelSole’s optimally persistence patterns), without introducing model adequacy assumptions into the analysis of the observations. These independently obtained slow manifolds of observations and simulations could then be compared statistically. Statistical inference gets a bit more complicated (because the slow manifolds generally are nonlinear functions of the data), but this is not a fundamental problem because resampling methods can be used in the statistical comparison of observations and simulations. This would have the benefit of clearly showing model inadequacies. It can be done with small ensembles of simulations (or just one simulation) because ensembles are not necessary to estimate slow manifolds reliably (as the animation above shows for observations).
Tim: The discriminant analysis you are describing seems to be exactly the predictable component analysis for predictability studies of the second kind (the relation to optimal fingerprinting is briefly discussed here). But I am confused about your statement that it is surprising that the forced-to-unforced discriminant analysis finds only one forced pattern, if you compare a forced and an unforced simulation. In two-group LDA when the group-means have to be estimated, there is only one degree of freedom for discrimination (Fisher’s linear discriminant: the inverse of the within-group covariance matrix times the difference between the group means). So why would you expect to find more? It seems to me to distinguish more “climate signals” (different signatures of different forcings), you would need to compare more forced simulations, each incorporating a different forcing, with an unforced simulation.
Tapio: The discriminant analysis I was describing was *not* LDA, which tests for a difference in means and has only one degree of freedom, but rather, the version that test for a difference in variance and generates as many discriminants as vector dimension (perhaps I am using the wrong terminology?). The version I was describing is more analogous to your discriminant analysis paper, in which the two data sets are low-pass and high-pass time series, except that in my case the two data sets are the twentieth century run and the pre-industrial control run.
In regards to whether fingerprinting is optimal, I agree that studies that use trend maps or spatial filters have the limitations you point out, but other studies analyze the data in a different way that avoids these limitations. For instance, one can define the forced response by a sequence of 10-year means. In this case, no linear trend assumption is made, rather, the evolution of the response is defined by the model. In addition, this evolution can be expressed by the leading extended EOFs (based on 10-year means), in which case no explicit spatial filtering is applied. Finally, Allen and Tett (1999, Climate Dynamics) proposed the “residual consistency test,” which tests whether the residuals about the forced response have the same variance as predicted by the control runs. In this way, the assumption that the models adequately simulate natural variability can be checked (to some extent).
I think your idea of using slow manifolds to identify model inadequacies is good. I tried to do this to some extent in the recent paper I mentioned– I identified a slow manifold from the control runs (which turned out to be highly correlated with the AMO), and then compared the autocorrelation time scale of this component in observations and twentieth century runs. I found that the observed value was “in the middle” of the values produced by the models.
To help orient some readers: There are things one can do with the observations alone and others that one can do with observations + simulations. My post was focused on “exploratory” analyses of the instrumental temperature data with no reference to GCMs. Tim’s comments refer to the problem of how best to use simulations and observations together to separate forced from internal variations, a fundamental problem about which quite a bit has been written lately and to which I want to return (if only to force me to read some of these papers more carefully). I would second Tapio’s point that there is value in developing new exploratory analyses, keeping these separated more cleanly from simulations.
Isaac is right. I apologize for not sticking within the boundaries of your problem Isaac! I should have explained why I didn’t stick with observations and avoid models completely. There are two reasons.
First, when we say we are interested in “low-frequency” variations, we are implicitly saying we are interested in variations that have a large amount of low-frequency variance *relative* to the high-frequency variance. The key word here is “relative.” A simple counter example is white noise– white noise can have tremendous power at low frequencies, but we would not ordinarily characterize it as “low-frequency,” even if the absolute amount of power at low frequencies was larger than for any other variable. This logic implies that a measure of low-frequency variability must be some ratio of low-pass to high-pass variance. After that, the details of the low- and high-pass filtering do not seem to be important. For instance, the patterns produced by optimal persistence analysis (as described in my paper that Isaac mentioned) are nearly the same as those produced by Tapio’s method, provided they are applied to the same data (I verified this some time ago when Tapio kindly provided me his imputed data set). The reason they are nearly the same is because both methods effectively maximize the ratio of low-pass to high-pass variance (the fact that optimal persistence analysis does this is shown in here ). If the problem is to seek alternative methods for finding low-frequency variability, and the approach is to maximize some ratio of low-pass to high-pass variance, I question whether it is productive to consider different definitions of “low-pass” and “high-pass,” because (1) different measures give similar results and (2) there is little a priori basis for deciding between different measures of “low-pass.”
Second, as Isaac mentioned, since observation-based discriminants capture a combination of the forced response and free low-frequency variations, you end up with a mixture of free and forced variations. There really is no way to avoid this contamination when deriving weights using only observational data. To avoid this contamination, one must go outside data and define properties of the forced response that can be used to discriminant it from unforced fluctuations. This is possible with models.
Tim, how about doing the discriminant analysis with the spatial gradient of temperature, rather than the temperature itself (motivated by the idea that spatial gradients are more relevant for the circulation), or analyzing the surface temperature and pressure simultaneously, or working with the difference between cold half year and warm half year temperatures, rather than their sum, etc. I just think there are a variety of exploratory analyses that have the potential to provide new perspectives on the surface instrumental record.
I am very interested in your thoughts in this area. One point to recognize is that discriminant analysis has the remarkable property that the maximized ratios are invariant to linear, non-singular transformations. This means that taking spatial gradients and then performing discriminant analysis should not lead to larger ratios than performing discriminant analysis on the original data, since spatial gradients are merely a linear transformation of the data. (There are a couple of technicalities I am ignoring here; e.g., we usually maximize in the space spanned by the leading principal components, and gradients are not invertible.)
The problem with adding variables is that it increases overfitting problems, which means you have to compensate for the additional variables by using fewer principal components. But, with long model runs, overfitting can be overcome. The question I would like to hear more about is which combination of variables would you say ought to provide the best discrimination of low-frequency or forced variability? (Was this your original question?) The few cases I’ve explored did not improve discrimination power. Working with cold half year and warm half year would be equivalent to including seasonal information, which actually works well. I did this in the paper you refer to in your original post.
A very small point and rather OT and a pet peeve.
The not uncommon extension of the Stefan-Boltzmann to grey bodies where it does not hold.
An example is the construction of an effective emissivity, and then to carry on as if the fourth power law still held blind to the effective emissivity being itself a function of temperature.
From what I can remember the positioning of the atmospheric window would (if nothing else changed) gives emission rising faster than the fourth power due to the motion of the spectral peak towards the window. OTOH increasing water vapour changes the shape of the spectrum in a way that tends to counteract this producing something more akin to a linear response.
Whatever the precise real world effect their assumption of an effective fourth power law is not sound. Sorry I am not saying you do it. It just irks me.
My impression is that the consequences of non-grey radiation when the tropospheric temperature change is assumed to be uniform in the vertical is not as important as differences in the vertical structure of temperature change in high and low latitudes, and the differences in cloud feedbacks.
Isaac,
Sorry I was making a much narrower point. That being:
even if everything else remained the same except for a uniform rise in temperature, there is no reason to assume a fourth power law.
I was also ambiguous, I meant that the grey body approximation doesn’t hold in the real atmosphere.
Because the SB law is the result of integration of the Planck function over all frequencies for unit emissivity, the correct equivalent is to integrate over the product of the Planck function and the emissivity function. As the later is also a function of frequency and temperature one is unlikely to end up with a neat function such as a fourth power law.
I believe that any non isothermic atmosphere containing GHGs is more or less guaranteed not to follow a fourth power law.
Well that is what I think.
I was not disagreeing with other effects being more significant, simply querying whether assuming a fourth power law tends to an overstatement of that particular effect.
I am a bit puzzled as to how this works.
Dealing with the data for just one calendar month:
As I see it there is a data matrix X and some weighting vector u whose product is the canonical variate c.
The discriminating pattern v is obtained by regressing X on c. Correct?
The maximisation principle consists in essence in splitting c into high pass and low pass components say h(c) and l(c) and varying u until the ratio R = V[l(c)]/V[h(c)] is maximal, where V[·] is the variance operator. Correct?
So I must imagine that u adds weight to those grid points which as a set are highly correlated at low frequencies and poorly correlated at high freqencies and also have significant low frequency variance and not too much high frequency variance.
Now I don’t think u is actually displayed in the paper and it strikes me that it may have some peculiar properties. The case reminds me of a story line about a town being the perfect bellwether for political polling purpose, so nowhere else needed polling. If a super R maximising grid square existed u could have only one non zero element however unlikely such an occurrence might be.
I am sure I will have more questions but for now I am interested to know if u is sparse or more broadly just a few grid cells contribute most of its variance, and if it can and does take on negative values?
Alex
Alex: Temperature variations generally have long-range spatial autocorrelations, in particular at low frequencies. So while it would be handy if a “super R maximising grid square existed,” this is very unlikely. The weight vectors u indeed have large-scale structure. For example, for the first canonical variate that maximizes R for the data in the animation at the top of the page, the weight vector u generally gives greatest weight to Northern Hemisphere ocean grid points, except in the North Atlantic (which exhibits substantial decadal variability). Land surfaces are weighted down (many land areas have weights close to zero, others have negative weights). There are also large ocean regions in the Southern Hemisphere with negative weights (e.g., in the South Pacific).
Mathematically, you can see that the scale of variations in u is large from the relation v ~ S u, where S (up to a scaling matrix) is the covariance matrix of the data. The large-scale structure in u gives rise to the large-scale structure in the spatial patterns of temperature changes v (the long-range correlations represented by S lead to additional ‘smoothing’ of the structures in v).
See addendum to post above.
Tapio and Isaac,
Thanks for the clarification. I am gratefull for your giving of the additional graphic to us, that was generous.
I can now see that the weighting and discriminating patterns are quite distinct so the method has found something to chew on in the data.
I am innately suspicious of algorithms that minimize or maximize if they have free rein to mine the data. On reflection I can see that various steps, particularly the use of a PCs (giving you orthogonality) , should help to discourage them from latching on to some “thin” vector by a process of subtraction of similar vectors.
The weighting vector goes some way to answering the “how was it achieved” question, and the answer looks intriguing.
The use of many techniques, Regularization, PC truncation, Smoothing, Discriminant Analysis, does not make for an easy read, and I am not sure how much more detail I could easily extract or wish to. So I shall try to comprehend it at some sort of conceptual level.
As I understand it, what you have achieved is a separation of the signals into high and low frequency components, of which you keep the low frequency part, by selection of optimal measurement weights (that is the obvious bit). What is not so obvious is why this is better than filtering. The clever bit seems to be that a process of cancelling out unwanted noise by taking advantage of the spatial element avoids the temporal dispersion inherent in filtering, i.e. it maintains zero phase shift in the frequency domain. Thereby you may have achieved quite a sharp or high order low pass separation without producing nasty high Q resonances with their associated temporal distortions.
If that is right then it might be important to know that the weighting vectors will maintain there noise “cancelling” properties, i.e. that they are inherent properties of the system (of a geographic origin) not opportunistic vectors. It might be good to know if the GCMs for which some have logged many centuries of data do exhibit weighting vectors that are stable from century to century and run to run.
Many thanks
Alex
Alex: I liked your concise summary of discriminant analysis.
You’ve hit on a problem with discriminant analysis that worries me a lot, namely, the fact that the weight vector is sensitive to the number of PCs (or more generally, sensitive to the degree of regularization). For “short” climate time series, the weight vector typically develops more short scale variability as the number of PCs increases. Given this sensitivity, it is dangerous to interpret the weight vector literally because it can change dramatically when the number of PCs change. Despite this sensitivity in the weighting pattern, the discriminant pattern itself is nearly independent of the number of PCs, beyond a certain threshold, so it is clear it is extracting a robust pattern. What happens is that as more PCs are included, discriminant analysis typically assigns order one weight to the extra PCs, but then these PCs get damped strongly when the weight vector is multiplied by the covariance matrix to obtain the discriminant pattern (as described in Tapio’s May 7 post). It is surprising to me that there are few studies of this sensitivity and of the reliability of methods for selecting the number of PCs (at least as far as I am aware).
Tim,
Thanks, my intuitive insight, such as it is, harks back to when I knew something of acoustics and how to exploit the spatial and hence temporal variations of the acoustic field by the positioning of microphones which are in turn commonly discriminant by design.
I shied away from Tapio’s description of the relationship between the spatial vectors through the application of the covariance matrix but I think I am getting it.
I am impressed that a discriminate approach works yet I do worry that I am ignorant as to what has been achieved. Visually it looks like a slow component (~60yr) has been discriminated against, or at least not enhanced along with the underlying trend. Were that to be true then it must surely share much ot its spatial pattern with discriminated against fast components such as ENSO. But no matter for I am getting a bit beyond my reach.
As, (or if), we progress with mitigation then an ability to detect the effect of mitigation by lifting it out of the noise by techniques more sophisticated and timely than simply waiting for the medium term trend to emerge would be hugely beneficial.
Alex
Alex: To add to Tim’s comment, the results of the analysis here are not very sensitive to the kind of regularization employed. Of course, as in any rank-deficient or ill-posed problem, one has to be judicious in the choice of regularization approach and parameters. We used truncated principal component analysis with determination of the truncation parameter by generalized cross-validation. But using, for example, reasonable fixed values of the truncation parameter gives similar results. As Tim mentioned, higher-order principal components give rise to smaller-scale variations in weight vectors (because of the relation between principal component analysis, or singular value decomposition, and Fourier analysis of convolution operators). But they generally are not associated with coherent slow variability.
Your broader question is about how to assess the significance of any slow component of climate variation identified with this approach. Since the analysis does not make explicit use of the time ordering of the data, one can assess the significance of any slow component by bootstrapping (repeating the analyses on resampled versions of the dataset, in which time is scrambled). This gives the confidence bands in the plot above. Any time variations of the canonical variate that are coherent and outside these confidence bands are indicative of true slow variations (rather than overfitting).
The advantage of the discriminant approach over simple point-by-point time filtering of the data is, as you note, that it uses the spatial covariability of the data and thus creates a more efficient filter. Testing it with long control simulations from climate models (without anthropogenic forcing) gives the expected null result of smaller ratios of slow (interdecadal) to fast (intradecadal) variance. Such results could be used as the basis for climate change detection.