Posted on June 29th, 2011 in Isaac Held's Blog
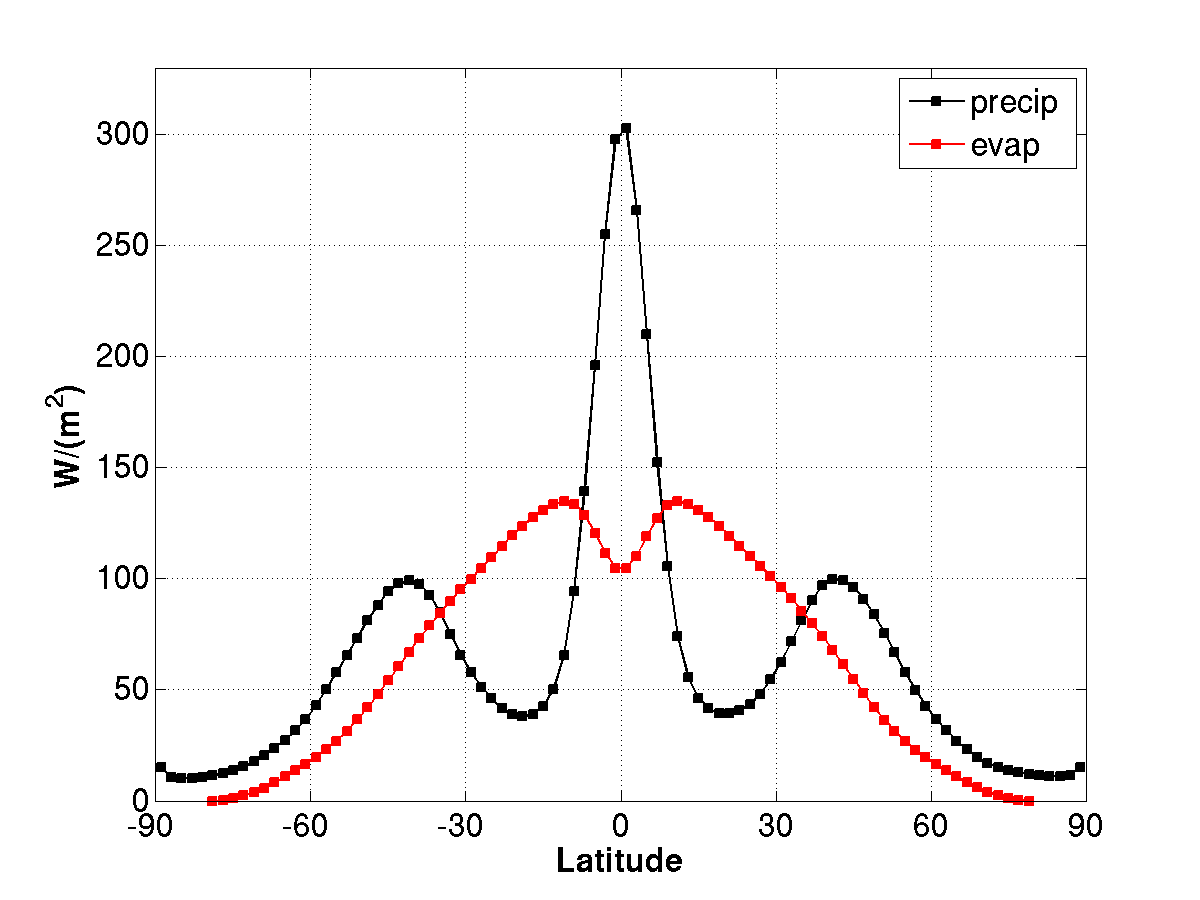 Time-mean precipitation and evaporation as a function of latitude as simulated by an aqua-planet version of an atmospheric GCM (GFDL’s AM2.1) with a homogeneous “slab-ocean” lower boundary (saturated surface with small heat capacity), forced by annual mean insolation.
Time-mean precipitation and evaporation as a function of latitude as simulated by an aqua-planet version of an atmospheric GCM (GFDL’s AM2.1) with a homogeneous “slab-ocean” lower boundary (saturated surface with small heat capacity), forced by annual mean insolation.
One often hears the statement the “strength of the hydrological cycle” increases with global warming. But this phrase seems to mean different things in different contexts.
The total amount of water vapor in the atmosphere has been increasing over the oceans, as clearly seen in the SSM/I microwave measurements of column integrated water vapor. The increase is as expected from the observed increase in ocean surface temperatures and the assumption of fixed relative humidity in the lowest 2-3 kms of the atmosphere, where most of the vapor resides, and is very consistent with atmospheric model simulations in which one uses the observed ocean temperatures as a boundary condition (e.g., Fig. 1 in Held and Soden, 2006). This increase is a consequence of the increase in saturation vapor pressure with temperature; it has nothing directly to do with the “strength of the global hydrological cycle” — by which I mean the globally averaged value of precipitation or evaporation. We need to avoid statements like “water vapor increases because of increased evaporation as climate warms”.
Globally averaged, precipitation balances evaporation (plus transpiration from plants) to an excellent approximation. To produce something like the observed rate of increase in vapor requires a sustained imbalance of roughly 0.002%. This minsicule difference obviously cannot be directly observed. In any case, it should be thought of as caused by the increase in atmospheric water, rather than causing it.
Think of a bucket (containing vapor) with “evaporation” filling the bucket, the overflow being “precipitation”. Now make the bucket bigger — but very slowly as compared to the time it takes evaporation to fill the bucket. If we hold evaporation fixed, precipitation will adjust by decreasing a tiny bit as the content of the bucket slowly increases while remaining full. Or let evaporation decrease; the content of the bucket will still increase as before as the bucket slowly grows. Analogously, it is not hard to generate a situation in a climate model in which temperatures warm and water vapor increases while evaporation and precipitation decrease in the global mean (one can increase carbon dioxide while increasing the amount of absorbing, non-scattering aerosol).
A better picture results if we assume that there are a lot of buckets moving around, each representing the saturation vapor pressure of different air parcels, and that they change their size depending on the temperature of the air in which they find themselves. If a bucket makes an excursion upwards it cools and contracts, then expands to its original size when it returns to its previous pressure and temperature. (Think Alice in Wonderland.) A lot of vapor is lost, to precipitation, when the bucket shrinks, so it is only partially filled when it returns. We should also assume that the rate of evaporation depends on the fullness of the bucket when it nears the surface — an empty bucket results in high evaporation, with the rate of evaporation slowing as the bucket fills. The strength of the global hydrological cycle can then be thought of as regulated by the frequency and amplitudes of the up and down excursions of the buckets, which control how empty the buckets typically are when they approach the surface. But what determines the statistics of these vertical motions?
Without trying to paint a full picture, I’ll just note that the dominant terms in the energy budget of the free troposphere, the region above the planetary boundary layer, are the radiative cooling and the latent heating associated with condensation. The easiest way to increase the strength of the global hydrological cycle in a model is to increase the net radiative cooling of the free troposphere (for example, by reducing absorbing aerosol or decreasing cirrus cloud cover). The dynamics of how this radiative cooling affects vertical motions, near surface humidities and evaporation might be intricate (more cooling => destabilization of the troposphere => more vertical excursions => more precipitation to balance the cooling, and also drier air entrained into the boundary layer => more evaporation) but you can’t easily avoid energy balance constraints. The controls on the strength of the global mean hydrological cycle are very different from the controls on the water vapor itself.
But when people say that the strength of the hydrological cycle is increasing, they are not necessarily referring to global mean evaporation or precipitation; sometimes they are referring to the redistribution of water by the atmosphere from one region to another.
Starting near the surface in the subtropics, where a lot of evaporation occurs, there are various kinds of air trajectories that can be thought of determining the pattern of precipitation. Some trajectories stay close to the surface as they move equatorward and then move upwards as they reach the “intertropical convergence zone (ITCZ)” marking the tropical rain belts. Others are swept polewards and upwards by midlatitude storms, creating the precipitation maxima marking the storm tracks. Buckets return relatively empty to the subtropical surface from either direction, helping to create an evaporation maximum in the subtropics. The distribution of precipitation and evaporation in an idealized version of GFDL’s AM2 atmospheric model with a zonally symmetric (longitude independent) lower boundary and, therefore, a zonally symmetric climate, is shown in the figure at the top.
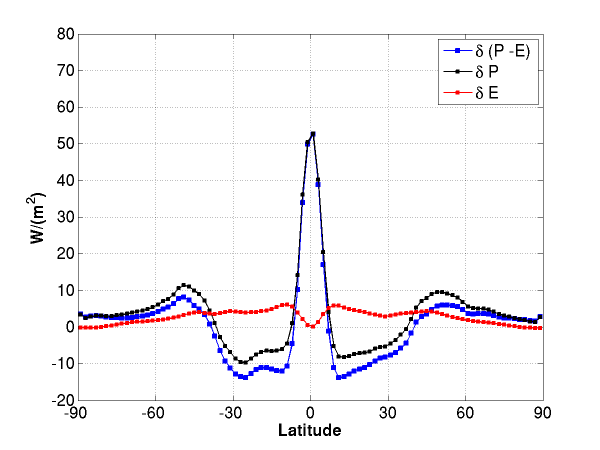
Now increase CO2 in this idealized model and let it’s climate equilibrate (which it does in a few years because the ocean has been replaced by a thin vertically homogeneous immobile slab of water). The result is that temperatures and water vapor increase while relative humidity doesn’t change much. Neither do the statistics of air trajectories change very dramatically, so buckets are still moving polewards and upwards from the subtropics into midlatitudes, shrinking by about the same proportions as before, but now dropping out more water because the buckets are bigger. So we expect the pattern of precipitation minus evaporation (P-E), which balances the convergence of the net atmospheric water flux, to be enhanced. As shown in the following figure, this is what happens in this model. Evaporation changes are relatively small (but see Wentz et al 2007), so the change in P-E is a good first approximation to the change in P.
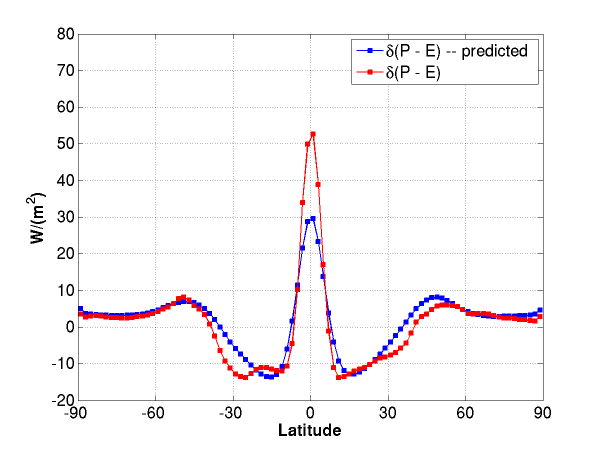
 And one can predict the change in P-E pretty well from the change in temperature and the increase in saturation vapor pressure. The “prediction” in the following figure refers to the assumption that the model’s moisture fluxes increase proportionally to the increase in lower tropospheric (700-100omb) saturation vapor pressure.
And one can predict the change in P-E pretty well from the change in temperature and the increase in saturation vapor pressure. The “prediction” in the following figure refers to the assumption that the model’s moisture fluxes increase proportionally to the increase in lower tropospheric (700-100omb) saturation vapor pressure.
This argument is more compelling outside of the tropics, where the motions carrying water vapor around are created by dynamics that is only secondarily affected by the latent heat release occurring in this process. In the tropics, latent heat release is an integral part of the dynamics causing these vertical motions, so there is no particular reason to assume that trajectories in the tropics will remain more or less the same if latent heating changes substantially. The figure suggests that the polar edges of the subtropics, near 30 degrees latitude, are drying out more that expected on the basis of this simple fixed flow, fixed relative humidity argument. In fact the Hadley circulation is expanding a bit, and, it seems, air trajectories are now bringing water into the ITCZ from somewhat further away, enhancing the ITCZ precipitation.
It is confusing to refer to this increase in water fluxes, causing increasing gradients in P-E, as an “increase in strength of the hydrological cycle”. An “increase in water fluxes within the atmosphere” is more understandable and more accurate.
The regional redistribution of precipitation due to the increase in atmospheric flux scales with the change in temperature. In fact, since the pattern of temperature change tends to be quite similar in different models, this redistribution tends to scale, across models, with global mean temperature change — that is, with climate sensitivity. One often hears the question “who cares about global mean temperature?”, but regional precipitation changes are more closely related to changes in global mean temperature than they are to changes in the global mean hydrological cycle.
Regional precipitation changes are certainly sensitive to regionally specific changes in circulation as well. An idealized GCM such as the one used here for illustration, with its homogeneous lower boundary, serves to isolate those aspects of the hydrological response that do not depend on local meteorology and boundary conditions.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Do the simulations presented in this post include a representation of the ocean energy transports in the tropics? If so, that may be the primary factor leading to the subtropical evaporation maximum. If not, then I suspect the evaporation minimum at the equator is due largely to the cloud distribution (Sobel, Adam H., 2003: On the Coexistence of an Evaporation Minimum and Precipitation Maximum in the Warm Pool. J. Climate, 16, 1003–1009.).
In atmospheric GCM simulations that neglect high clouds (or do not have clouds at all), neglect ocean energy transports, and have annual-mean top-of-atmosphere insolation, I have not obtained an evaporation maximum in the subtropics. These simulations feature some of the factors thought to be favorable to determining such an evaporation distribution like the velocity statistics that lead to dry air in the subtropics (discussed in this post) and weaker surface winds at the equator than in the subtropics. Presumably these favorable factors cannot overcome the larger net surface shortwave radiation at the equator than in the subtropics in these simulations.
There is no prescribed ocean heat transport in the model. The model has clouds — this is the full AM model (actually it is an old version, AM2.0, that I happened to have a plot from lying around). But I suspect that the evaporation minimum at the equator here is due primarily to a minimum in the surface wind speeds.
How do you view Wentz et al. ?
(This is my second attempt — my reply earlier today was a little incoherent.)
It’s very important if true and would be telling us that there is something going on in the tropospheric energy balance that the models are not capturing. Putting aside trends, the results suggest that models are not capturing the increase in global mean (or tropical mean) precipitation during ENSO episodes. We don’t understand the tropics very well, so there’s certainly room for surprises Here’s a recent paper that might give you some of the flavor of the discussion. Clarifying how well models simulate the response of global mean precipitation to ENSO seems like the highest priority to me.
I’m getting a late look at this, and it is very interesting. I think you really put your finger on it that people don’t really have a good definition when they say ‘intensified hydrologic cycle.’ Unfortunately, loose definition of the strength of the hydrologic cycle makes your statement “regional precipitation changes are more closely related to changes in global mean temperature than they are to changes in the global mean hydrological cycle” a head-scratcher.
A lot of people have developed hydrologic models that use air temperature as a proxy for energy available for evapotranspiration, but people using that paradigm are likely to be quite surprised by how low the change in evaporation is (your second figure). The spatial redistribution of precipitation, on the other hand, is striking.
Brent, in the statement that you quote, the “global mean hydrological cycle” simply refers to the global mean evapotranspiration or precipitation. Not sure why you consider this statement a head-scratcher. Local temperature changes within the troposphere are closely related to the global mean temperature (because the response to well-mixed greenhouse gases tends to have a pretty well-defined spatial structure. Typically, models that warm more globally also warm more locally. especially in the free troposphere. This local warming controls the increase in horizontal moisture flux, to first approximation, leading, in this simple aqua-planet model to the pattern of precipitation change in the figure.