Posted on July 8th, 2011 in Isaac Held's Blog
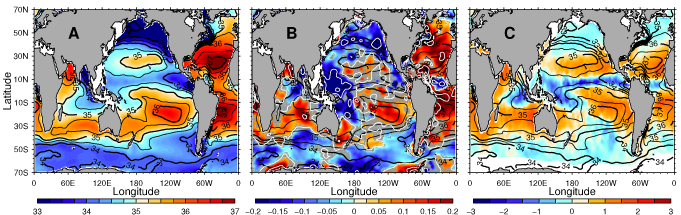 From Durack and Wijffels, 2010: A) Climatological surface salinity (0.5 pss contour), averaged over 1950-2000; B) the linear trend over these 50 years (pss/50 years) ; and C) the NOCS Southampton estimate of net climatological freshwater flux from ocean to atmosphere (m/yr).
From Durack and Wijffels, 2010: A) Climatological surface salinity (0.5 pss contour), averaged over 1950-2000; B) the linear trend over these 50 years (pss/50 years) ; and C) the NOCS Southampton estimate of net climatological freshwater flux from ocean to atmosphere (m/yr).
In post #13, I discussed the argument that warmer temperatures => more water vapor in the atmosphere => more transport of water away from regions from which the atmosphere habitually extracts water, and more transport to regions into which the atmosphere habitually adds water. The consequence is the expectation that “the wet get wetter and the dry get drier” if by wet/dry we mean regions with precipitation (P) greater than/less than evaporation (E). In that post, I effectively ignored the presence of land. Land introduces a variety of complications that make this kind of argument more difficult, most obviously because of the constraint that P must be greater than E on the time scales of interest (ie. changes in water storage on land can be ignored and runoff must be positive). I am going to continue to ignore the existence of land (and glaciers) in this post!
What is the evidence for trends in P or E or P-E over the oceans? Trends in the ocean salinity field promise to provide a test of our understanding — it is also helpful that the oceans provide a low-pass filter to noisy precipitation signals.
Oceanic salinity is driven by changes in the net fresh water input at the surface, P-E. (It is also forced by river discharge from the land and from melting icecaps.) Salinity is a tracer, carried by the oceanic flow and ultimately subject to molecular diffusion on the smallest scales. It cares only about the redistribution P-E and not P and E individually. This is convenient since, as discussed briefly in post #13, the constraints on how the the global mean P or E might change with warming are very different from the constraints on the changes in P-E, and it is helpful to test our understanding of these things separately.
The oceanic flow redistributes salinity through a mix of advection by steady circulations and transport by coherent eddies, chaotic advection, and turbulent diffusion. But salinity is also an active scalar which affects the density of seawater and, through the equation of motion, changes the flow. This is especially important in sub-polar regions — because of the form of the equation of state of seawater, salinity is, in fact, the primarily factor controlling density in the relatively cold subpolar oceans. If we could also ignore this inconvenient fact, salinity would becomes a passive tracer and its dynamics linear, driven only by the surface flux of freshwater P-E.
Suppose that we are given the statistically steady salinity distribution of a control climate and then assume that P -E is perturbed. In fact, consider the simplest possible case in which P-E is simply multiplied by a global constant, as the crudest possible representation of increased atmospheric water transport accompanying warming. If the circulation changes significantly, there isn’t much we can do except to try to solve the full problem, coupling the salinity with the temperature and momentum equations — that is, to work with an oceanic GCM. But suppose we arbitrarily assume that the circulation does not change much, so that we can think of the salinity as passive and its equation as linear. Then the solution is just that the salinity is multiplied by the same constant multiplying P-E. The total salt in the ocean is unchanged, so what this means is that all spatial salinity gradients are multiplied by a constant once the system settles into a new steady state. (There are some small inconsistencies in this argument, partly resulting from the existence of the Goldsborough circulation — the circulation has to be perturbed to some extent to balance a change in the mass sources and sinks — but this circulation is small compared to the dominant oceanic currents driven by density gradients.)
Note that this does not mean that the distribution of P-E simply imprints itself on the surface salinity distribution without change in shape, even if circulation changed can be ignored. The advection-diffusion operator can make this relationship non-local. If the Atlantic is much saltier than the Pacific, then scaling P-E up, in this passive limit, will create an even larger gradient between the Atlantic and the Pacific, whatever combination of P-E distribution and circulation asymmetry can be thought of as generating this salinity gradient in the mean climatology.
Durack and Wijffels have recently presented an important new analysis of salinity trends over the past 50 years (see Figure and link at top of post.) The comparison of panel A, showing the climatological surface salinity gradients, with panel B, their estimated 50 year salinity trends, is striking. (Panel C shows an estimate of the climatological P-E pattern. The expectation is that estimates of oceanic salinity trends are more robust that any attempts at directly estimating trends in P-E over the oceans.) There is a correspondence in all major features between panels A and B, the upshot being that surface salinity gradients are, indeed, increasing throughout the world ocean. In particular, the average salinity difference between the saltier Atlantic and the fresher Pacific is increasing, as one would expect from the quasi-steady advective-diffusive response to a scaled up P-E pattern, with little change in ocean circulation. In the North Atlantic, the sub-polar gyre has a positive salinity trend (except along its western boundary), with no obvious sign of the freshening that might result from the reduced poleward salt transport from the subtropics that would accompany a weakening of the overturning.
To my eye, the trends in panel B are substantially larger than expected from Clausius Clapeyron and the roughly 0.5C warming over this time period. I am also a bit confused as to how long we should expect it to take for the Atlantic-Pacific salinity difference to respond to an increase in the magnitude of P-E, assuming that part of this difference is associated with the asymmetry of the circulation. (I would have guessed that circulation times scales of a century or more would be needed, but it looks like this inter-basin gradient is being enhanced at more or less the same rate as the intra-basin gradients.)
This salinity trend analysis is deserving of close scrutiny (especially regarding effects of inhomogeneities in data coverage through this time period) given its potential to serve as a centerpiece for discussions of changes in the hydrological cycle associated with warming.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac,
Could we infer from the pattern-lock ( or spatial phase-lock) of the long-term trend with the mean climate of surface salinity as in panel B – if it is true – that the same mechanism responsible for why the Atlantic is saltier in its mean state than the Pacific may also be responsible for its long-term variation? The ocean dynamics is equally important to the mean surface salinity pattern in the Atlantic ( Qu et al. 2001: What governs the North Atlantic salinity maximum in a global GCM? GRL doi 10.1029/2011GL046757 ). Possibly the mechanism ( the oceanic “salt river ” termed by P. Niiler) could be used to explain the departure of the surface salinity trend from the surface fresh water fluxes. Could also the pattern-lock phenomenon have important implications on the pattern of long-term climate change such as decadal and/or abrupt climate change?
Thanks to your last post which included very useful suggestions to my interest in the hydrological cycle research.