Posted on January 1st, 2012 in Isaac Held's Blog
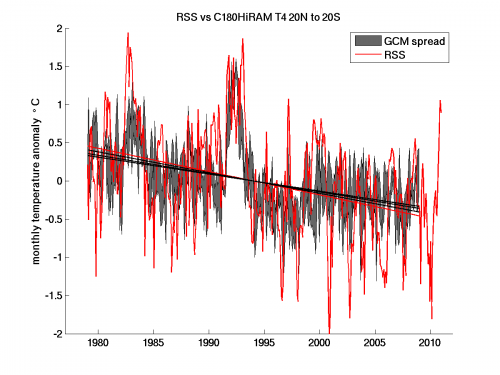
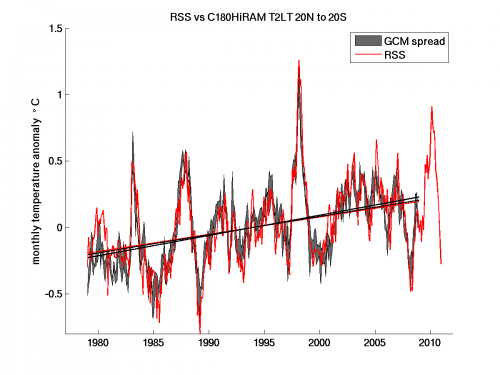Lower tropospheric MSU monthly mean anomalies, averaged over 20S to 20N, as estimated by Remote Sensing Systems – RSS (red) and the corresponding result from three realizations of the GFDL HiRAMC180 model (black) using HadISST1 ocean temperatures and sea ice coverage. Linear trends also shown. (Details in the post.)
Motivated by the previous post and Fu et al 2011 I decided to look in a bit more detail at the vertical structure of the tropical temperature trends in a model that I have been studying and how they compare to the trends in the MSU/AMSU data. The model is an atmosphere/land model using as boundary condition the time-evolving sea surface temperatures and sea ice coverage from HadISST1. It is identical to the model that generates the tropical cyclones discussed in Post #2 (and the animation of outgoing infrared radiation in Post #1). It has the relatively high horizontal resolution, for global climate models, of about 50km. Three realizations of this model, starting with different initial conditions, for the period covering 1979-2008, have been provided to the CMIP5 database, and it is these three runs that I will use in this discussion. The model also has prescribed time-evolving well-mixed greenhouse gases, aerosols (including stratospheric volcanic aerosols), solar cycle, and ozone. The atmospheric and land states are otherwise predicted.
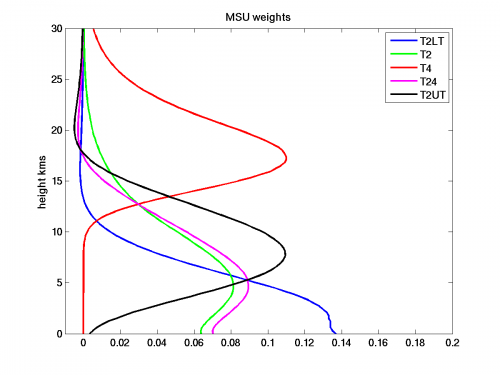
The MSU data, as gridded monthly mean anomalies, were downloaded from RSS. The weights for the channels referred to here are included in a figure at the bottom of this post — thanks to Qiang Fu and Celeste Johanson for help in this regard. All of the model results are monthly mean anomalies from the model’s seasonal cycle defined as the time mean for each month over the 30 year period Jan 1979- Dec 2008. Observations are plotted as anomalies from a time average over the same period. And all model and observed linear trends are computed over the same time interval as well (unless otherwise stated). I’ll only discuss averages over the deep tropics from 20S to 20N.
Analyzing an atmosphere/land model running over prescribed oceanic boundary conditions has advantages and disadvantages as compared to analyzing a model fully coupled with the ocean. The advantage is that one avoids conflating disagreements between model and observations regarding the variation in sea surface temperature (SST), on the one hand, with problems that the atmospheric model may have in coupling SST variations to the troposphere and land surface, on the other. And one can compare in much more detail the time evolution of quantities of interest — even if one’s coupled model is perfect, its El-Ninos will resemble reality only in their statistics.
The disadvantage is that one might be doing some damage to the atmosphere by disallowing two-way interactions with the oceans. The significance of this distortion is very much problem specific and can be subtle. For example, tropical cyclone intensity is presumably affected by running over prescribed SSTs, by not allowing the oceanic mixing generated by the storm to affect its intensity. If tropical cyclone intensity, in turn, affects the tropical lapse rate trends this would be a problem. I don’t, at present, see this or other related possibilities as significant for this lapse rate issue, but its something to be alert for.
Let’s start with the lower tropospheric channel referred to as T2LT or TLT. The red line in the figure at the top is the RSS MSU time series, while the shading spans the results from the 3 model realizations. (The smallness of this spread shows how tightly the tropical lower troposphere is coupled to the ocean surface in the model. This spread would be much larger in a fully coupled model). Trend lines are shown for both the observations and the three model runs (it is hard to see the 3 distinct model trend lines because of overlap). I get 0.130 C/decade for the RSS trend and 0.148 for the mean of the 3 model runs — with 0.154, 0.137, and 0.152 for the individual runs). If I drop the first two years, 1979 and 1980, the mean model trend drops to 0.143 and the RSS T2LT rises to 0.149. (It might be a consequence of how I plotted this, but this early period does seems to be a major source of the discrepancy. You can think of this as cherry-picking or as a very crude way of judging whether this difference is plausibly significant.)
Moving on to the deeper tropospheric average provided by T2 (also referred to as TMT), we get a very similar looking plot:
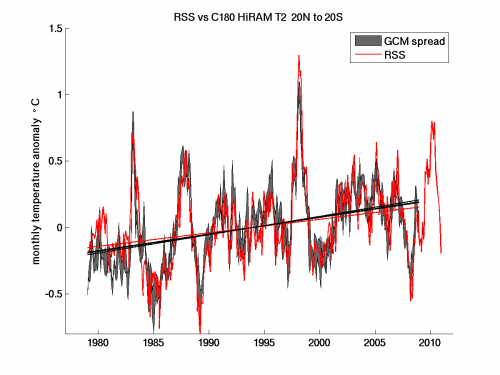The model trends are now (0.138, 0.125, 0.129) with a mean of 0.131, with the RSS trend over this period is 0.102. These trend are smaller than the T2LT trends, in both the model and the observations, despite the fact that T2 weights the lower troposphere less strongly that T2LT. The model trends actually increase with height through the troposphere. The problem, long appreciated, is that T2 has significant weight in the stratosphere, where there is a cooling trend in both model and observations as indicated here by the T4 time series:
The warming due to absorption by El Chichon and Pinatubo aerosols is superposed on an uneven cooling trend. The El Chichon signal is relatively weak in the model, contributing to the underestimate of the cooling trend. (The model is also missing substantial internal variability — it does not simulate a realistic Quasi-Biennial Oscillation, but his does not appear to be the dominant signal in this missing variability). Here I follow Fu et al 2011 and use T24 = 1.1*T2- 0.1*T2LT (oops — I meant T24 = 1.1*T2- 0.1*T4; June 8, 2012) to reduce the influence of the stratosphere on T2. A plot of T24 would look a lot like the that for T2 above, but the mean model trend is increased to 0.168, while the RSS T24 trend is 0.143. The model-0bs difference here is smaller than for T2 itself because the model’s cooling trend in T4 is smaller than that observed.
The actual model trends as a function of height are shown here, along with the trends using the T2LT and T24 weighting functions. To try to capture the model’s upper tropospheric warming better, I have defined T2UT = 2*T24 – T2LT to get something that follows the upper troposphere a little more closely (see the weights at the bottom of the post — you want to avoid negative weights while keeping the integral of the weights unchanged). (I have arbitrarily plotted the satellite channel trends at the pressure levels at which model versions agree with the model trend: T2LT = 700mb, T24 = 550mb, T2UT = 450mb.) The red dots are the RSS values. Also shown at 1000mb in magenta is the trend in SST and, by the three black dots, the land+ocean mean surface trends in the 3 realizations — all over the 20N-20S region.
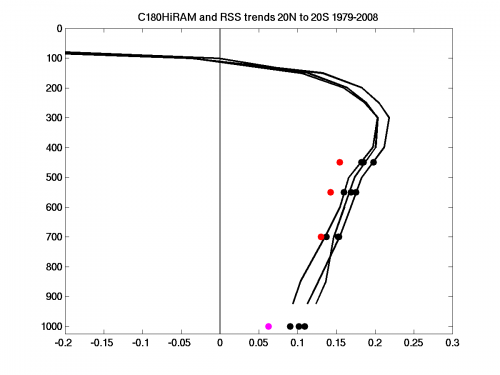There is substantial spread in the land warming, associated (I think) mostly with rainfall variability in semi-arid regions — I doubt that the effects of this variability propagate upwards beyond 700mb or so.
For fun, I also generated the same figure after dropping the first two years from the analysis, with this result:
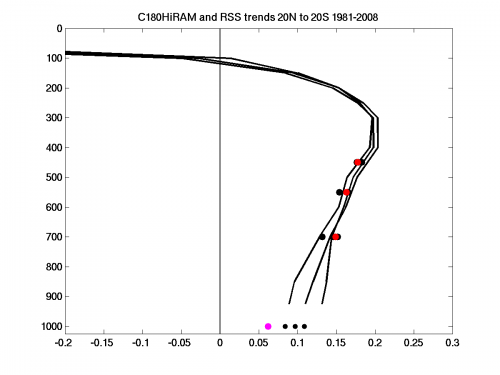The difference between these two plots is not small. A bias of the sort seen in the first plot, with the tropics evidently being destabilized as compared to the model, would have substantial consequences for tropical meteorology if extrapolated into the future.
Let 
This is just one model and one observational analysis. (See Thorne et al, 2011 for a recent discussion of differences between alternative analysis of the MSU data, and inconsistencies between radiosondes and MSU.) Accepting this comparison at face value, it is still not clear to me if there is a significant model bias or not, when the SSTs are specified. The differences seem subtle, but small differences in lapse rate can have important effects on tropical meteorology.
I would like to encourage more analysis of these prescribed SST (“AMIP”) simulations in this context. Most of the recent model-data comparisons of tropospheric lapse rate trends focus on coupled models. Especially in the tropics, biases in forcing or climate sensitivity make themselves felt to a large extent through the SSTs. Superposing the bias due to SST differences on any biases due to the internal atmospheric dynamics controlling tropical lapse rates can be confusing. Normalizing tropospheric trends by surface ocean trends can help in this regard, but this assumes that the tropical mean SST is the only thing that matters, which need not be the case.
It is also nice to be able to focus on specific time periods in a way that would not be possible in free-running coupled models generating their own ENSOs, the detailed time histories providing potential insights into the data sets as well as the models. Are the early years in this record (1979-1980 roughly) also the source of model-data disagreement when other AMIP models are examined? Can we determine whether these differences are due to problems in the MSU data, the SST input into the models, or model biases?
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]
Hi, Isaac,
About half of the discrepancy between AR4 GCMs and MSU observations in T24-T2LT trends for 1979-2010 is caused by the overestimation of AR4 GCMs tropical mean surface trends while another half by the difference in the ratio of T24/T2LT (Fu et al. 2011). The second half is of interest in terms of the vertical structure of the tropical temperature trends. T24/T2LT (T2UT/T2LT) is about 1.1 (1.2) from observation but 1.2 (1.4) from AR4 GCMs.
Your analyses using GFDL AGCM (HiRAMC180) runs provide important insight to the understanding of the discrepancy between AR4 GCMs and MSU observations in the ratio of T24/T2LT or T2UT/T2LT: By constraining the spatial distributions of SST trends using the observations, the ratio of T24/T2LT (T2UT/T2LT) becomes about 1.14 (1.28) that is much closer to those from observations. Here it might be important to emphasize that it is the surface spatial trend pattern instead of tropical mean surface trend that makes the difference (the ratio should not be sensitive to the tropical mean surface temperature trends).
As another note, the ratio of T2UT/T2LT is 1.12 (UAU) and 1.2 (RSS) from MSU observations, 1.29, 1.33, and 1.22 from GFDL HiRAMC180, and ranges from about 1.3 to 1.5 from AR4 GCMs. It seems suggest that there might be a systematic bias in simulated SST spatial trend patterns in AR4 GCMs (this need to be confirmed by analyzing more AGCMs simulations).
Qiang
Qiang — thanks — it will be interesting to see if there is a systematic difference in the upper level amplification associated with the pattern of the SST change in atmospheric models. One could use as boundary condition the SSTs generated by the coupled models over this time period, rather than observed SSTs, to address this.
Isaac,
the earliest two years is an interesting issue. In a GRL piece in 2007 we showed that starting in 1979 led to an outlier in terms of amplification behavior in the observations compared to almost any other choice of similarly long period. In part this may highlight the limitations of fitting a linear model to a system that is not simply linear (given that the value is within the spread from a model (AMIP also if memory serves correctly) ensemble this seemed plausible). Or it may highlight some real physical process. People seem obsessed over the end-point issue only at one end (the present) whereas arguably the far more interesting end-point is the start in 1979 vis-a-vis other potential start dates.
Did your AMIP runs go back prior to 1979 and can you compare those early period series to MSU equivalents calculated from radiosondes. Specifically it would be of interest to see whether the very marked step-like change in the mid-1970s tropospheric average temperatures is replicated in the AMIP runs.
Thorne, P. W., D. E. Parker, et al. (2007). “Tropical vertical temperature trends: A real discrepancy?” Geophys. Res. Lett. 34(16). Article Number: L61702 DOI: 10.1029/2007GL029875
Peter — thanks for the reference and comments.
These particular AMIP runs do not go back further in time.
I did not say much in the post about the relationship between mean surface and tropospheric trends — partly because I find the influence on the mean tropical lapse rate of convection over land, with its big diurnal cycles, confusing. In this fixed SST model, there is still substantial variability in land temperatures across the realizations. To the extent that one can think of the land warming as forced by the ocean warming, is it more useful to look at the ratio of ocean warming to tropical-mean tropospheric warming? Have you or anyone generated something like your Fig 1 normalizing T2LT by mean oceanic warming?
I can certainly see that the choice of time interval affects the trends in the data or in a model realization, but it is not as clear that it should affect the difference between a model with prescribed SSTs and the data.
Isaac,
the first paper that explicitly recognized the tight coupling to my knowledge was Santer et al., 2005. There we used the tropical average over land and ocean. In a couple of more recent papers it has been argued that the tropical troposphere is likely driven by the tropical oceans (Santer et al., 2008, Thorne et al., 2011). I have long argued that given the tight constraint we should normalize the model amplification behavior estimates by the observed surface changes. In the CMIP3 ensemble there is an order of magnitude spread in surface trends which yields a large spread in tropospheric estimates and the multi-model average tropical surface warming is roughly twice that observed making a comparison to the multi-model coupled average meaningless. You would expect a difference under such circumstances and in fact not finding a difference would be significantly more problematic scientifically than finding one. On the other hand if we undertake first a transform so we scale the model amplification behavior in each run by the surface trend and then compare to the observed tropospheric trends we get a more physically insightful result. The alternative is AMIP style runs as you do here of course.
Santer, B. D., T. M. L. Wigley, et al. (2005). “Amplification of surface temperature trends and variability in the tropical atmosphere.” Science 309(5740): 1551-1556.
Santer, B. D., P. W. Thorne, et al. (2008). “Consistency of modelled and observed temperature trends in the tropical troposphere.” International Journal of Climatology 28(13): 1703-1722.
Thorne, P. W., P. Brohan, et al. (2011) “A quantification of uncertainties in historical tropical tropospheric temperature trends from radiosondes” Journal of Geophysical Research – Atmospheres, doi:10.1029/2010JD015487
For the avoidance of doubt I should clarify that this only applies to the deep tropics where convection is the dominant vertical mixing process. In other regions it is far from clear whether tropospheric temperature changes should be greater than, the same as, or less than surface changes. So, it doesn’t follow that surface changes should be amplified aloft globally …
Isaac,
In a paper by myself and David Neelin, we looked at some of these issues on somewhat shorter timescales, interannual and shorter over the last few decades. We compared profiles of temperature anomalies, regressed onto the free-tropospheric vertical average temperature anomalies, to a theoretical curve calculated using a series of reversible moist adiabats. The idea was to normalize by overall temperature change without relying on local boundary layer values, which may be somewhat decoupled from the free tropospheric changes. We got values that were extremely close to the moist adiabatic values for NCEP-NCAR reanalysis for basically all tropical regions and for monthly and daily anomalies (with the exception of the easterm Pacific for daily data). For daily AIRS satellite data (over two years) there were still good correlations but the regression coefficients were somewhat higher than the theoretical curve at midlevels and lower in the boundary layer; radiosondes during TOGA-COARE over the Pacific warm pool showed this behavior as well; monthly data looked closer to the moist adiabat, at least in the free troposphere.
Christopher E. Holloway and J. David Neelin, 2007:
J. Atmos. Sci., 64 (5), 1467-1487. doi:10.1175/JAS3907.1
https://journals.ametsoc.org/doi/abs/10.1175/JAS3907.1
We also looked at 3 models from CMIP3 used in the IPCC AR4, although this was not in the paper; it is in my Ph.D. dissertation, located on (Figure 2.14 on page 52). The models matched very closely to the moist-adiabatic curve for 25 years of the historical climate runs (this was over the warm pool but was also true for the tropics as a whole). We also did a simple profile of differences over a century of the climate change runs, and you can see almost the same shape of warming for that time scale.
We figured that the models, like the NCEP-NCAR reanalysis, are probably somewhat too constrained by their convective parameterizations, causing them to follow the moist-adiabatic curve too closely. But we know that the models are also doing this for shorter-term variability, and observations seem to validate a lot of this link to the moist adiabat on these shorter time scales.
Chris, thanks. I think we can all agree that the relevance of the moist adiabat on shorter time scales, plus the intrinsically short time scales of tropospheric adjustment, requires us to look very carefully at evidence that suggests departures from this behavior on longer time scales.
Hi, Chris and Isaac,
Although it was not presented in our GRL paper, we found a nearly constant T24/T2LT ratio on the interannual time scale from AR4 GCMs which agrees excellently with that from the MSU observations. This enforces your results and statements. Note that the tropical tropospheric temperature variability on the interannual time scale is dominated by the ENSO while in last thirty years the warming mainly occurs in the Atlantic ocean, and to less extent over Indian Ocean and West Pacific.
Qiang
Isaac:
Someone directed me to your interesting post. I have some comments as this is a topic with which I’m all too familiar.
1. In several papers, summarized in Christy et al. 2010, we and others investigated the accuracy of the various tropical upper air temperature datasets in detail. It was shown that RSS contained spurious tropical warming in the 1990s due to the overcorrection for the diurnal cooling that characterizes the drifting afternoon spacecraft. RSS was clearly the outlier (see Fig. 4.) Thus, using RSS as the comparison does not represent the real observational evidence and portrays too much apparent agreement.
2. The comparison in the posting above does not contradict the evidence in our papers that the CMIP3 models overstate the amplification ratio. The HiRAMC180 comparison is using a model, but tightly constrained by real temperatures, i.e. an AMIP style run. The CMIP3 coupled model runs show more warming than actually occurred in this time period (globally about twice too much) with a tropical amplification factor around 1.37 (ratio of trends Tlt/Tsfc, see Fig 10 in Christy et al.)
3. In the runs of your model I see a TLT trend of +0.148 C/decade for 1979-2009. Observational tropical trends, as published, are +0.09 +/- 0.03 C/decade, producing an amplification ratio of 0.8 +/- 0.3 (Christy et al. 2010.) The HiRAMC180 model indicates a scaling ratio (using trend of Tsfc as +0.12 C/decade) of 1.23 – a little less than the typical GCM, but outside of the observed ratio.
4. The same comments apply to T2 (RSS has some extra warming not found in the other datasets except for STAR which was examined in detail in Christy et al. 2011 and found also to have instituted RSS’s diurnal correction, so suffers from the same problem as RSS.) Thus the red dots in your Fig. should be accompanied by many others further to the left (see our Fig. 10).
5. With much misinformation on this issue I want to indicate that any model/observation comparisons should be normalized (i.e. such as using the amplification ratio to eliminate variations due to volcanoes and ENSOs) and use the full tropical surface temperatures (rather than say SSTs only.)
6. Perhaps the first paper that recognized the tight coupling between tropospheric layers temperatures and the surface was Christy and McNider 1994 .
Thank you for the post and the opportunity to provide information that evidently was not used in your post.
Christy et al. 2010, What do observational datasets say about modeled tropospheric temperature trends since 1979? Rem. Sens., 2, doi:10.3390/rs2092148.
John, thanks for taking the time to comment. Here are some responses to the points that you raise:
My motivation in this post was the narrow one of reacting to Fu et al 2011, and I used RSS so as to relate to that paper. I did not mean the post to read as an endorsement of one product over the other. Here is a link to Christy et al 2010 to make it a bit easier for readers to access. Glancing at the figure at the top of my post, I don’t see anything from the model/RSS comparison to hint that there is less agreement after 1991, but this obviously requires a closer look. Biases in TLT ans SST data sets should be independent, so I would very much appreciate it if someone could point me to studies suggesting non-stationarity in their covariability, or non-stationarity in AMIP model biases, with the hope of indentifiying or supporting arguments for one product over another.
An idea I was trying to push in this post is the use of AMIP rather than fully coupled models so as to separate the effects of model/obs differences in SSTs from differences in vertical coupling. Avoiding the need to adjust for ENSOs or volcanoes is precisely my point
I personally think that it is more useful, when thinking about coupling of the surface with the troposphere in the tropics, to use only SSTs and not land temperatures. There are good reasons why we typically constrain only SSTs (and sea ice) in these AMIP runs. The difference in characteristic time scales in atmosphere and ocean makes it plausible that decoupling of the two doesn’t create too many problems (and I think the detailed agreement, at higher frequencies than the trend, in the figures in the post is evidence of this) — but land and atmosphere vary on the same time scales so decoupling them can cause a variety of problems. I am skeptical that specifying land temperatures somehow in this kind of model would be helpful in model/data comparisons. I would argue that it is better to think of land together with the troposphere as responding to SST variations–as discussed also in post #11, and when normalizing tropospheric trends with surface trends, I would rather see normalization by the SST trends only
With regard to the strong coupling between surface and troposphere, I was first exposed to this by Pan and Oort, 1983 based on radiosondes.
Hello Dr. Held,
In order to consider the body of evidence, readers should also consider Santer et al. (2011), Thorne et al. (2011a,b). In the unlikely chance you have not already read those papers then I highly recommend them as they supersede Christy et al. (2010) and do not necessarily support their findings. In fact, as I noted at SkepticalScience:
“……evidence that has been published the past year or so that showed model predictions are consistent with observations when one takes the inherent uncertainties into account or notes that there are still outstanding issues with the satellite tropospheric temperature estimates (e.g., Thorne et al. (2011a), Thorne et al. (2011b), Mears et al. (2011)).
Dr. Christy appears to be of the opinion that the satellite data (in particular the UAH data) are the metric to use against which to validate the models, but a recent paper by Mears et al. (2011) finds that there are probably unresolved issues with the satellite estimates. Christy and Spencer also have a long history of being overconfident in their product and dismissing concerns about biases in their product– I have documented that here.
From Thorne et al. (2011a):
“It is concluded that there is no reasonable evidence of a fundamental disagreement between tropospheric temperature trends from models and observations when uncertainties in both are treated comprehensively.”
From Santer et al. (2011):
“There is no timescale on which observed trends are statistically unusual (at the 5% level or better) relative to the multimodel sampling distribution of forced TLT trends. We conclude from this result that there is no inconsistency between observed near-global TLT trends (in the 10- to 32-year range examined here) and model estimates of the response to anthropogenic forcing.”
Again from Santer et al. (2011):
“Given the considerable technical challenges involved in adjusting satellite-based estimates of TLT changes for inhomogeneities [Mears et al., 2006, 2011b], a residual cool bias in the observations cannot be ruled out, and may also contribute to the offset between the model and observed average TLT trends.”
From Mears et al. (2011):
“As we move higher in the atmosphere, the radiosonde-satellite trend differences tend to increase. For TMT,
only about 50% of the radiosonde trends lie within our error bars, except in the northern extratropics, where the radiosonde network is the most spatially complete, and thus the adjusted data sets, which in almost all cases rely upon a neighbor constraint, are most likely to be reliable. Here the agreement remains good. For TMT, the STAR trends are consistently larger than RSS but generally just within our uncertainty bounds when diurnal adjustment uncertainties are included, while the UAH trends are less and tend to be outside our calculated error margins with the exception of the southern extratropics where the two data sets are in good agreement.”
Mears et al. conclude:
“It is clear from this comparison that many hitherto unexplained differences between the data sets, many of which have been previously documented, remain. Although the internal uncertainty estimates derived herein lead to consistency between a number of estimates there are nearly as many cases where differences between the RSS product and competing estimates cannot be reconciled as being caused solely by RSS data set internal uncertainties. An inescapable conclusion from this is that the methodological choices that we and others have made have lead to a substantial and significant impact upon the resulting estimates.”
Yes, of course, no model is perfect. But neither are the data, so we need to keep in mind that the satellite data (or radiosonde data) have their own issues and be open to the likelihood that those issues, when addressed, may bring the models and observations into even better agreement. As noted by several researchers it is not advisable to think that one dataset alone (e.g., UAH) represents the “truth”, because as noted by Thorne et al. (2011):
“No matter how august the responsible research group, one version of a dataset cannot give a measure of the structural uncertainty inherent in the information.”
As I said in response to Dr. Christy’s comment, my intention here was not to try to sort out the differences between the UAH and RSS temperature trends. What I was trying to do — this does not seem to get through very clearly — is argue that one is better off using AMIP simulations, with prescribed SSTs, rather than coupled models, when addressing issues about model biases in lapse rate trends. Santer et al (2011) use coupled models, as do most recent studies. Due to internal variability in the models and in nature, one ends up with large sampling uncertainties that prevent one, unnecessarily, from making much sharper statements. Unless someone can convince me otherwise, I think working with AMIP models that, as shown in the plots above, produce negligible variability in tropospheric trends, is far better — allowing us to study the details of these time series, and the consistency between SSTs and MSU temperatures, and not just the overall trends. Biases in SST trends strike me as a very different issue, for which bringing in estimates of internal variability is crucial.
Hello Dr. Held,
Thank you for your reply. You make some valid points. For what it is worth, I agree with your approach.
This may be off topic, but recently some people have been making claims that the climate models are on the “verge of failing”[Knappenberger] or that the IPPC models “are close to being refuted” [Pielke Senior]. I would be very interested in your thoughts on whether or not such confident conclusions/assertions are warranted.
Our models are deficient in all sorts of ways, of course, some minor and some more troubling, which is why there is so much ongoing work to try to improve them. I’ll return to surface temperature evolution, which I presume is what is being referred to here, and transient climate responses in GCMs, in future posts.