Posted on January 21st, 2012 in Isaac Held's Blog
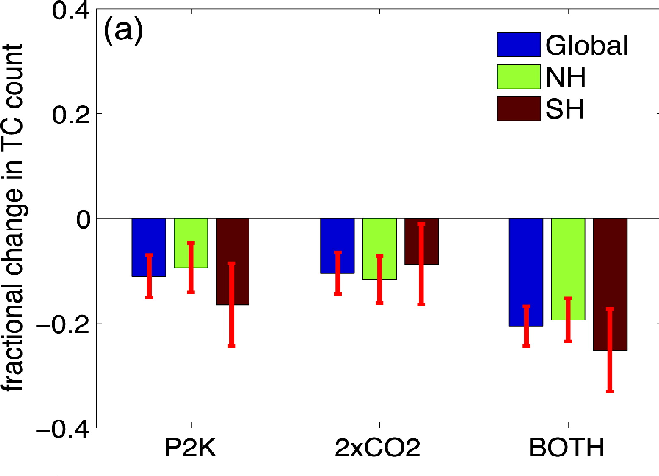 From Held and Zhao 2011, a simulation with an atmospheric model of the change in the number of tropical cyclones that form over each hemisphere and over the globe when sea surface temperatures (SSTs) are raised uniformly by 2C (labelled P2K), when the CO2 is doubled with fixed SSTs, and when SSTs and CO2 are increased together.
From Held and Zhao 2011, a simulation with an atmospheric model of the change in the number of tropical cyclones that form over each hemisphere and over the globe when sea surface temperatures (SSTs) are raised uniformly by 2C (labelled P2K), when the CO2 is doubled with fixed SSTs, and when SSTs and CO2 are increased together.
Suppose that we have a model of the climatic response to gradually increasing CO2, and we examine the globally-averaged incoming top-of-atmosphere flux, , as a function of time (using a large ensemble of runs of the model to average out internal variability). Letting
refer to the difference between two climate states, for example the difference between the climates of 2100 and 2000 in a particular model, we end up looking at an expression like
where is the global mean surface temperature and
refers to all of the other things on which
depends. Here
is the CO2 concentration, or, to the extend the useful range of this linearization, log(CO2). The forcing
might be defined as
. We typically go a step further and write
so that we can think of this last term as a feedback, modifying the radiative restoring strength,
i.e, so that . While this is a formal manipulation that you can always perform if you want to, it is obviously more useful when
is actually more or less proportional to
. Ideally, there is a causal chain:
=>
=>
. But what if the change in
due to an increase in CO2 results from some other causal chain that doesn’t pass through the warming of the surface (or the warming of the strongly coupled surface-troposphere system)?
The classic example is the cooling of the stratosphere due to increasing CO2. This cooling has no direct connection to the surface/tropospheric warming. If there were a strong negative cloud feedback, say, that prevented the surface/troposphere from warming, the stratospheric cooling would be hardly affected. But this stratospheric cooling does has a substantial effect on , the energy balance at the top of the atmosphere — let’s call it
where
is a measure of the stratospheric temperature response. The standard procedure is to include this term in the forcing, so that we retain an expression of the form
, with
This has the advantage of maintaining the simple forcing-feedback picture, but at the expense of a more complicated expression for the forcing.
An alternative way of justifying this redefinition is to include, as part of the forcing, all responses that effect the energy budget very quickly — before the surface temperature responds substantially. This is what I referred to as the ultra-fast response in post #11 (ultra-fast = atmosphere in isolation – a month or so at most; fast = ocean mixed layer; slow = response of bulk of ocean; ultra-slow = even slower). In practice, one can try to estimate the forcing after the ultra-fast adjustment has taken place in a couple of ways. Using a full coupled atmosphere-ocean model, one can increase the CO2 instantaneously, at t = 0, and watch how the ensemble mean responds, extrapolating back to t=0 to estimate the forcing. The point here is not to look in detail at the ultra-fast response in the first month or so, but to extrapolate back using the “fast” relaxation characterizing the warming of the ocean surface — ie, plotting
vs
and extrapolating back to
(as in post #5). An alternative procedure is just to increase the CO2 in an atmosphere/land model with fixed ocean temperatures and sea ice as boundary conditions and examine
in the equilibrated state. The first alternative seems more secure in that it is not subject to possible distortions due to decoupling atmosphere from ocean, but it may suffer from some fuzziness in the extrapolation if the distinction between ultra-fast and fast adjustments is not as sharp as we might like.
For the case of the stratospheric temperature adjustment to CO2, you can avoid addressing this issue head on because, to first approximation, you can look at the energy balance at the tropopause rather than the top of the atmosphere. But it has become clear from the analysis of GCMs in the past few years that there is a potential for ultra-fast responses to CO2 in the troposphere as well, particularly in the cloud field — see Gregory and Webb 2008, Colman and McAvaney, 2011, and Andrews et al 2011. The result is that a part of the cloud change in a typical climate change scenario scales with the warming of the surface and another part does not, effectively scaling instead with the CO2 itself. Letting stand for the cloud field, we have formally
. This splits the naive “cloud feedback” in the original analysis into two terms, moving one of them, the ultra-fast part that is realized before substantial temperature change occurs, into the forcing — leaving a remainder that scales with the surface warming and can usefully be thought of as a feedback.
The ultra-fast cloud response seems to be mostly confined to solar reflection from low clouds, at least in the Colman-McAvaney paper — which is also what I see in a quick look at some aqua-planet simulations with one of our models. What is the mechanism? I’m not sure –it’s not clear to me whether land-ocean contrasts are the key, or whether open-ocean processes that can be studied with aqua-planet simulations capture the main mechanisms. A CO2 change causes immediate changes in infrared fluxes, and these changes in fluxes can effect clouds in the absence of significant temperature changes — by changing the radiative cooling from cloud tops or the subsidence of air in the tropics (the adiabatic warming associated with this subsidence closely balances the radiative cooling) — both of which can effect low cloud amounts. I’ll leave further discussion of the dynamics of the ultra-fast cloud response for another time (maybe I’ll understand it better then).
Models’ ultra-fast responses in precipitation have been discussed fairly extensively, partly with geoengineering in mind. Ming Zhao and I have recently looked at the ultra-fast response of tropical cyclones to CO2, by fixing SSTs and increasing CO2 in the model discussed in post #2. For doubling of CO2 with fixed SSTs, we get about a 10% reduction in the number of tropical cyclones averaged over the globe, as shown in the plot at the top. These results may very well be model dependent at present – for example, Yoshimura and Sugi, 2005 get a larger reduction in the same setup. Almost all models show a reduction in global mean tropical cyclone numbers in global warming simulations, in which CO2 and SSTs are increasing together. In our results, only about half of this global mean reduction is related to the warming.
Is any of this important? Between the fast times scales on which the oceanic mixed layer equilibrates and the slow time scales on which the deep ocean heat uptake saturates, the climate response tends to be proportional to the forcing itself, with a proportionality constant that depends both on the strength of the radiative restoring and on the efficiency of the heat uptake by the oceans. That is, in , one can set
so that
. See post #3, where I refer to this frequency band as the “intermediate regime” and argue (following many others) that it is relevant both for 20th century simulations and for 21st century projections. But if
is proportional to
and, therefore, to
(assuming the forcing is dominated by CO2), this extraction of part of the cloud response that scales with
rather than
is irrelevant. Testing this decomposition with observational trends also becomes very difficult.
Geoengineering is the place where this distinction is most clearly relevant. If one is successful, through solar management, say, in preventing warming, one still has to deal with consequences of the CO2 increase that are not dependent on the warming.
Also, consider the standard idealized scenario where CO2 increases up to some point and then is held fixed at that level thereafter. During the increasing phase, the ultra-fast responses are mixed in with the temperature-dependent responses, but after equilibration of CO2, we would see the effects of the remaining warming without the overlay of the ultra-fast response to CO2. With respect to cloud feedback, this makes it harder to connect transient and equilibrium responses quantitatively .
I have already discussed in (post #5) an unrelated problem in connecting transient and equilibrium sensitivities — the potential for change in the strength of radiative restoring due to change in spatial structure of the warming as the system equilibrates. To the extent that we don’t understand these things, it is that much more difficult to use evidence that bears on equilibrium sensitivity (primarily paleo) to constrain the transient climate response, and vice-versa.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac,
The recent paper, ” Fast and slow timescales in the tropical low-cloud response to increasing CO2 in two climate models”, by Watanabe et al. might also be of interest.
Jianhua, thanks — that does look very relevant
One mechanism for ultra-fast cloud response that is discussed in Andrews et al 2011, Section 6.3, is the “physiological forcing” effect of CO2. This phrase refers to the tendency of plants to close their stomata under elevated CO2, altering the surface energy balance over land to a state with more sensible and radiative cooling, and less latent cooling. As discussed in Doutriaux-Boucher et al 2009 and Andrews et al 2011b, this shift in the partitioning of surface energy fluxes over land happens very rapidly, and results in a reduction of low cloud fraction over land (at least in these models…). This mechanism is also discussed in a more idealized context by Betts and Chiu 2010 (though they do not address issue of timescale, since physiological forcing occurs within the PBL over land, one would expect it to act rapidly and directly in response to CO2, and not to care about changes in SST). I think the question you pose, regarding to what extent aquaplanet simulations show similar responses, is very interesting, and would be more surprising than ultrafast CO2 responses over land.
Tim, we do see evidence of cloud responses in an aqua planet version of our model with prescribed SSTs — almost 0.5 W/m2 in shortwave reflection for CO2 doubling — but we haven’t had a chance to analyze it. It will be interesting to see if other aqua-planet runs show anything similar.
Dear Prof. Held,
This is slightly off topic, but you write above,
“This cooling [in the stratosphere] has no direct connection to the surface/tropospheric warming. If there were a strong negative cloud feedback, say, that prevented the surface/troposphere from warming, the stratospheric cooling would be hardly affected. But this stratospheric cooling does has a substantial effect on N, the energy balance at the top of the atmosphere…”.
Reading this came as a big surprise to me. I have been told that the cooling in the stratosphere is one of the key indicators that humans are causing global warming. But, if there is no relationship between the cooling in the stratosphere and the human contribution to warming at the surface, then I don’t understand how stratospheric cooling could be even relevant to ‘what is causing global warming’. Surely, it would just prove that we are adding CO2 to the atmosphere – which is not disputed.
If you had time to clarify this, I would be most grateful. Do you think the stratospheric cooling is relevant to the IPCC conclusion that, “most of the observed increase in global average temperatures since the mid-20th century is very likely due to the observed increase in anthropogenic greenhouse gas concentrations”?
Alex, I think you have understood my comment correctly.
More generally, suppose A and B are two parts of the climate system, both of which respond to CO2, but we happen to be focused on reducing the uncertainty in the A-response. If A and B are strongly coupled, then it should be obvious that you want to take into account your ability to model the B-response when estimating your uncertainty in the A-response. But consider the limiting case that A and B are totally uncoupled. Observations of ocean acidification do not provide any obvious constraints on the surface temperature response to CO2. This example reminds us that it is not just the fact that they are uncoupled that makes the B-response irrelevant to constraining the A-response — you also need to assume that the dynamics of the two responses are unrelated — in this case, the carbonate chemistry controlling the pH trends has no connection to the feedbacks controlling climate sensitivity. Getting the former right does not give us more confidence in the latter.
Stratospheric temperatures are not as cleanly decoupled from surface temperature as the ocean pH — there are interesting couplings going from stratosphere-to-troposphere and from troposphere-to-stratosphere that are the subjects of an extensive literature. For example, surface/tropospheric warming in models could have an effect on the stratospheric Brewer-Dobson overturning circulation by affecting the waves that propagate from the troposphere and drive this stratospheric circulation. But none of these connections are strong enough to suggest (to me) that simulations of stratospheric cooling help constrain climate sensitivity significantly. (I guess things could get more subtle and interesting as one approaches the tropopause — could the height of the transition from warming to cooling in the tropics be correlated with climate sensitivity?)
I guess this depends partly on one’s priors. Both the stratospheric and tropospheric responses have radiative transfer as their starting point, so if you question the basics of our understanding of radiative transfer, then your confidence in tropospheric responses should be affected by the simulation of stratospheric cooling. But if, like me, you have no reason whatsoever to doubt the basics of our understanding of the relevant radiative transfer, I don’t see how simulations of stratospheric cooling can help much in discriminating between models with very different tropospheric responses to CO2 due, say, to different cloud feedbacks.
Isaac,
“I’ll leave further discussion of the dynamics of the ultra-fast cloud response for another time (maybe I’ll understand it better then).”
I hope your understanding comes soon! As a new reader of your blog, your ongoing series of posts regarding sensitivity timelines (or response timelines) is fascinating. I hope some of this type of material makes it into the AR5 as from my POV, having been mostly a consumer of media reporting of the IPCC ARs, I perceive there to have been too much focus on equilibrium climate response (though certainly the ARs themselves contain plenty of projectsions of “X warming by X year”.
That’s enough for now….
BillC
As you’ve noticed, I am trying to build a case for less of an obsession with equilibrium climate sensitivity.