Posted on February 13th, 2012 in Isaac Held's Blog
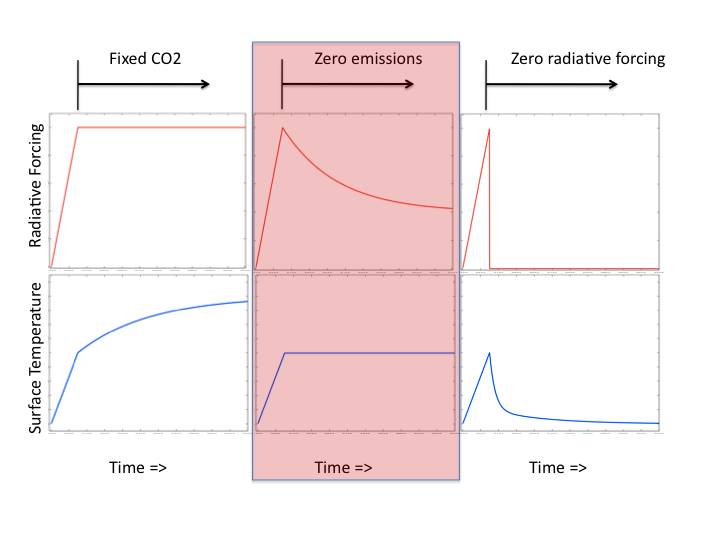
Schematic of three different idealized global warming scenarios. The time period is roughly 1,000 years and each scenario starts with the CO2 increase and warming from the anthropogenic pulse of emission in the 20th and 21st centuries. On the left, emissions are slowed so that CO2 is maintained at the level reached at the end of this pulse. In the center, emissions are eliminated at the end of the pulse, resulting in slow decay of CO2. On the right, CO2 levels are abruptly returned to pre-industrial levels —perfect geoengineering — a scenario useful for isolating the recalcitrant component of warming discussed in post #8.
If we stop emitting CO2 at some future time how would surface temperature evolve over the ensuing decades and centuries — ignoring all other forcing agents? This question (or closely related questions) has been looked at using a number of models of different kinds, including Allen et al, 2009, Matthews et al, 2009, Solomon et al, 2009, and Frolicher and Joos, 2010. These models agree on a simple qualitative result: global mean surface temperatures stay roughly level for as long as a millennium, at the value achieved at the time
at which emissions are discontinued, as illustrated schematically in the middle panels above.
This simple result emerges from a cancellation between the climate response to CO2 perturbations and the CO2 response to emissions. If the CO2 in the atmosphere remained at the level attained at time , then the surface would continue to warm as the deep ocean equilibrated and the heat uptake by the ocean relaxed to zero. This increase from a transient response with substantial heat uptake to a response with an equilibrated deep ocean is the fixed-concentration commitment.
However, when emissions are eliminated, the CO2 in the atmosphere does not stay fixed, rather it decays slowly. This decay does not take the system back to pre-industrial CO2 levels, since full equilibration requires transfer of carbon to sediments and crustal rocks, which requires far more than a millennium. We can imagine the airborne fraction of the emitted carbon as evolving in time, from a larger value before , perhaps comparable to that observed in recent decades (about 45%), and then asymptoting, after roughly 1000 years, to a smaller non-zero value.
The papers listed above suggest that the reduction of airborne fraction from the current value to this equilibrated value more or less compensates for the additional warming that would be experienced with fixed CO2. Additionally, the time scale of the adjustment of this airborne fraction and of the relaxation of the ocean heat uptake to zero are roughly the same — they are both controlled in large part by the physical mixing of shallow oceanic waters into the deeper oceans. This similarity in the slow adjustment time scale, and the coincidence of the rough cancellation of the fixed concentration warming commitment with the reduction in airborne fraction, combine to make plausible the relatively flat surface temperature response.
One could make a long list of things that could upset this picture, dramatic changes in land surface carbon uptake/release being an excellent example. In any case, it will be interesting to see what emerges from new generations of Earth System Models when applied to this idealized scenario.
It is worth keeping in mind that sea level, for example, will respond very differently in this zero-emission scenario — the component due to thermal expansion continues to rise on these time scales, in all of these models, as the surface warming penetrates further into the ocean. It is also worth keeping in mind that the temperature response to short-lived forcing agents, such as methane, would look more like the right panel in the figure, with the temperature response peaking at the time at which emissions are curtailed.
To the extent that the response of climate to emissions is linear, as it presumably is for small enough emissions, we could write an expression for the response of any climate index to CO2 emissions,
:
where is the climate response at time
for unit emissions between the times
and
. (
is a time before which anthropogenic emissions are negligible.) If the problem can also be assumed stationary in time, then
is a function only of the time elapsed between forcing and response,
. The claim is not that this linear perspective is the final story, of course, but only that it may be a useful point of reference.
combines the response of climate to CO2 and the response of CO2 to emissions.
What might look like? Following the discussion above, for the global mean surface temperature we can imagine it looking as simple as
The fast relaxation time is the time required for both the temperature of the ocean surface layer and its CO2 concentration to equilibrate, treating the deeper ocean layers as infinite reservoirs of heat and carbon. A single relaxation time might not be adequate, but as long as the relaxation takes place fast enough, it would have little effect on the big picture except to smooth out the response to the high frequency component of the emissions. Might this
response function actually be more robust than the physical climate CO2
or carbon cycle
CO2 responses separately? If your model does not represent the time scale of the equilibration of the deep ocean adequately, this might, as mentioned above, have compensating effects on the shapes of the CO2
and
CO2 response functions, leaving the
response with the same relatively flat shape.
Ignoring the relaxation time , the implication of this simple form for the response is that the global mean surface temperature at time
can be thought of as simply the linear response to the sum total of past emissions
The implications of this result can be looked at as a glass half empty or half full. From a pessimistic perspective it says that, in the absence of geoengineering, we are committed for the next millennium to the warming that we have already created by past emissions. More optimistically, we could say that future surface temperature increases are due to future emissions — that is, it is not the climate system that has committed us to additional warming, but rather the inertia in the society and infrastructure producing the emissions themselves.
To the extent that this picture holds, we can also say that the emissions trajectory over time is not particularly important for where we end up — the climate in the year 2100, say, would depend on the total emissions between now and 2100 and not on how these emissions were distributed over the 21st century.
The ease of communicating this result is also worth emphasizing. Only one number is needed — — the warming per unit cumulative emissions. Typical central estimates for
in the papers listed above are in the range 1.5-2 degrees C per trillion tons of carbon emitted. Clearly, it is pretty important to know whether this simple picture is useful or misleading.
One final point. For the idealized scenario pictured in the central panel at the top of the post, the warming never approaches the value consistent with the equilibrium response to the maximum CO2 at the end of the anthropogenic pulse. To relate the sustained temperature response to the maximum CO2 we need to use the transient climate response (TCR). (See posts #4-6 for discussion of the TCR). I think this is another good reason to place more emphasis on the TCR in discussions of climate sensitivity.
[note added on Feb. 25, to make contact with some previous posts and to address an e-mailed comment:]
As the system equilibrates the spatial structure of the warming will presumably change, even if the global mean temperature does not. In particular, you would expect more polar amplification with time, especially in the Southern Ocean, where temperatures are very slow to warm (see figure at the top of post #11). On the other hand, tropical temperatures, which are more equilibrated, might cool over time. You can’t infer a whole lot from global mean temperature about things like the temperature of the oceans around the Antarctic ice sheet. See Gillett et al 2011.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac, thanks for this post. I agree that the linearity between emissions and temperature response makes an “emissions sensitivity” sensible to pursue, and could be very useful as a tractable and clear metric for policy-makers.
The one thing I have been more skeptical about is the virtual non-dependence between global temperature and declining radiative forcing (in the long term) in the zero emission scenario. It is certainly believable that if we keep the forcing constant, there will be more “warming in the pipeline” as the oceans warm up to equilibrium. Indeed, that is just basic physics.
But once we let this forcing decay (by ceasing emissions) then eventually the forcing will decay beyond whatever imbalance is currently keeping us at a non-zero net TOA flux. The weak slaving between global T and the changed RF seems only believable if the decaying forcing asymptoted toward whatever value would close the TOA energy balance at modern day conditions (i.e. the equivalent CO2 concentration that could result in a zero net TOA budget in the modern day with T held fixed). Once the forcing becomes more negative than this zero value, it would seem the climate would cool at a similar timescale as “heating in the pipeline.”
The Solomon study invokes the deep-ocean as a stabilizer to this, but it is not very intuitive, and seems to have very large implications between the time dependence of forcing and response in paleoclimates. Could you elaborate on this?
Chris — your comment ended up in the Spam folder — not sure why.
The key point in this idealized linear picture is precisely that the forcing does not drop below the value needed to equilibrate with the temperature achieved at end of the emissions pulse, because not all of the carbon is removed from the system by natural processes on this 1,000 year time scale. You seem to be describing a picture in which the carbon perturbation decays to zero.
Isaac,
If I have understood correctly, you are describing the temperature T(t) as the combined result of two response functions. One to get from emissions to forcings F(t) = f * E(t) and one from forcings to temperature T(t) = g * F(t). Where * is the convolution operator.
So T(t) = g*(f*E(t)) = (g*f)*E(t)
For T(t) to equal A times the integral of E(t) we need A = g*f
i.e. function pairs whose convolution is a constant.
Function pairs of the form
f(t) = m·t^a and g(t) = n·t^b where a+b = -1 m·n=A { · = multiplication }
give g*f = A as required.
As I recall the temperature response to forcing has been modelled as T(t) = g*F(t) where g(t) = n/Sqrt(t) or more generally n·t^b where b = ~ -1/2. This gives rise to a sort of law of squares asymptotic approach to equillibrium, I think Hansen and others have shown this.
So provided that f(t) =~ (A/n)·t^-(1-b) the temperature will track the total emissions as described
i.e. T(t) = ~ A·Integral[E(t)·dt]
This is likely to be the case provided that f(t) is long tailed which is thought to be the case as you show in your schematic (centre box top line).
The unceasing emphasis given to the equillibrium sensitivity is doubly sad, it is not something that we wish to verify and were a mitigation plan to be adopted it becomes redundant and transient response become what matters. It is important in a world were we do nothing which seems a terribly gloomy state of affairs.
Alex
You are correct that, taking this linear picture seriously, can be expressed as a convolution of a response function that generates radiative forcing from emissions, I’ll call it
can be expressed as a convolution of a response function that generates radiative forcing from emissions, I’ll call it 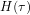 , and a function that generates temperature from radiative forcing, say
, and a function that generates temperature from radiative forcing, say  :
:
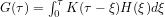 .
. and
and  equal to power laws is what you want to do.
equal to power laws is what you want to do.
I couldn’t follow your algebra completely, but in any case I don’t think that setting
This is probably more than most readers care to know, but when I try to make more explicit the simple picture I drew above — using a single slow relaxation time scale common to both carbon and temperature (rather than a diffusive picture that I think you are referring to) — assuming that the fast response is instantaneous to keep the algebra simple — and just thinking non-dimensionally about the shape of these functions — I get something like:
Interestingly, when I compute the convolution, and if I assume that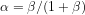 , I get a
, I get a  that is almost flat — it starts and ends at the same value but has a little bump —
that is almost flat — it starts and ends at the same value but has a little bump —  . If the relation
. If the relation 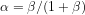 does not hold, then
does not hold, then 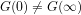 . Assuming that I got this right (which is not a safe assumption) this is a little surprising — my intuition would have been that
. Assuming that I got this right (which is not a safe assumption) this is a little surprising — my intuition would have been that  was the relevant condition.
was the relevant condition.
Hi Isaac,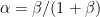 satisfies
satisfies  and your intuition
and your intuition 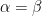 would be fine for small
would be fine for small 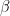 .
.
Your calculation seems right to me (unless I’ve misunderstood the context). The condition
Paul.
Paul, thanks — I managed to confuse myself because of the way that I wrote the relation between and
and 
Hi Isaac & Paul
It may not be clear to everybody why that relationship holds.
The limit of the convolution as t goes to zero, goes to the integral of H(tau) times the delta function which is just H(0) = 1. Only the delta function part of K(tau) matters as t goes to zero. The integral with the exponential part goes to zero and a convolution of a function with the delta function is just the funcntion which goes to H(0) = 1 as t goes to zero.
The integral of K(tau) converges rapidly to (1+beta), (1 from the delta function part and beta from the eponential part).
Because it converges rapidly and when only considering the limit as t goes to infinity we only need to consider H(t) as t goes to infinity where it is effectively a constant (1-alpha).
A convolution of a function with a constant is the same as the integral of the function times the constant (1+beta)(1-alpha).
The requirement that convolution takes the same value at both t = 0 and t – infinity gives the relation: 1 = (1+beta)(1-alpha).
Isaac,
Thanks, it is much clearer now.
Some aspects still concern me but that must wait. The notion that the mixing down of heat and CO2 share a common mechanism is very interesting but the effective reservoir size ratios of for heat and CO2 seem unlikely to be the same but I can see that the time evolution to equliibrium would be the same. A number of other factors would have to be shown to be small or to equate to an additional constant term in the combined response function.
I am trying to interprete K(tau) in terms that could be useful when setting up an energy balance equation normally given for a lumped thernal mass as:
As a convolution this I would write as:
The temptation is to generalise this to:
and substitute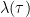 with the inverse (deconvolution with unity) of your
with the inverse (deconvolution with unity) of your  giving
giving
My apolgies to all for the jargon but it is not easy to express another way. Intutively has a similar effect to
has a similar effect to  increasing over time but
increasing over time but  has to be convolved with a forcing history to get a temperature and I need to go the other way so I need its converse which is its deconvolution with unity.
has to be convolved with a forcing history to get a temperature and I need to go the other way so I need its converse which is its deconvolution with unity.
I would then go on to add a function that accounts for the mixing down of heat in a way similar to the effect of your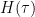 .
.
I would do eassentially the same thing for the CO2 response function, convolve the two response functions which each are sums of functions giving a long list of convolutions to be added up, each of which needs to be either to be constant (which includes just being very small) or can be added to other terms to form a constant.
That would be it in principle, if I could do it, my question is: does that seem to be the way to go?
Does it even make sense (my not making sense seems to be a growth market)?
I think I have added enough comments to allow it to by understood by others.
Thanks
Alex
“We can imagine the airborne fraction of the emitted carbon as evolving in time, from a larger value before T, perhaps comparable to that observed in recent decades (about 45%), and then asymptoting, after roughly 1000 years, to a smaller non-zero value.”
I believe that you are using the term “airborne fraction” incorrectly. Airborne fraction is the ratio of [emissions at time T] over [the change in concentration between time T and time T+1]. If emissions are zero, and the change is negative, the airborne fraction is technically zero (but in reality, I think is poorly adapted to such questions).
I think the term you are looking for is more like, “We can imagine the difference between the current concentration and preindustrial concentrations decreasing over time, starting at 120 ppm (or about 30%) today, and asymptotically approaching some non-zero value on the order of hundreds or thousands of years.”
-MMM
Maybe we need another term — something like “cumulative airborne fraction”.