Posted on February 28th, 2012 in Isaac Held's Blog
This post is concerned with arbitrariness in the terminology we use when discussing climate feedbacks. The choice of terminology has no affect on the underlying physics, but it can, I think, affect the picture we keep in our minds as to what is going on, and can potentially affect the confidence we have in this picture.
In feedback analyses of a climate response to some radiative forcing, we start with a reference response, the response “in the absence of feedbacks”, and then we look at how this reference response is modified by feedbacks. An electrical circuit analogy often comes to mind, with the reference response analogous to the unambiguous input into a circuit. But the choice of reference response in our problem is ultimately arbitrary. The following is closely based on the introductory section of Held and Shell 2012.
My starting point is the same as that for several other posts: an expression for the net incoming flux of energy at the top of the atmosphere. Here I am just going to think of the incoming energy flux as a function of three numbers, , where
is the forcing agent and where
and
are two other things that
depends on. Perturbing our forcing agent we define the radiative forcing as
. I’ll assume that
is positive. To establish a new equilibrium we need
or
.
We could stop here, treating and
on an equal footing. But suppose that we are mostly interested in
. (In fact, let’s suppose that
is the global mean surface temperature.) We no longer treat
and
in the same way but instead write the surface temperature response as
where and
is a measure of B-feedback. (In using this terminology, we are presuming that
can be thought of as proportional to
— see post #22). The reference response in the absence of B-feedback is just
. We can then write
where is a non-dimensional measure of the
-feedback.
Now I am going to make a choice for that may seem a little odd — I’ll choose
to be the tropospheric temperature. Most infrared photons escaping to space are emitted from the troposphere rather than the surface. If the troposphere does not warm, then to regain energy balance the surface has to warm by an order of magnitude more than if the tropospheric warming were comparable to that of the surface. If the surface and tropospheric responses are, in fact, comparable, this would be described as a large negative tropospheric feedback drastically reducing the magnitude of the reference response (the response at fixed tropospheric temperature).
This is clearly not the traditional formulation! The standard choice would be to set equal to the surface temperature minus the tropospheric temperature, so that
-feedback would become lapse rate feedback. The reference response is now the response you get in the absence of lapse-rate feedback and is now much smaller — and the feedback relatively modest.
But what is wrong with this tropospheric feedback picture? It doesn’t change the final answer — it just makes for a different decomposition between reference response and feedback. The main problem is that the no feedback limit, in this tropospheric feedback perspective, is not physically plausible. Warming the surface without warming the troposphere would destabilize the atmosphere, and atmospheric circulations would develop to transfer energy from the surface to the troposphere to fight off this destabilization. Atmospheric models of all kinds as well as observations (especially on interannual time scales) are consistent with this picture. By choosing an unphysical reference response, we end up with a framework in which the total response is a small difference between two large terms. It’s not that it’s wrong; it’s just not natural.
The picture becomes even more problematic if we add another effect to the mix, for example a positive surface albedo feedback that we would typically think of as modest. For a given size of the radiative effect of the albedo change per unit surface warming, , in (W/m2)/K, the non-dimensional measure of the strength of the feedback,
will be very large because the reference response,
, is very large if one uses the tropospheric feedback framework. One is effectively evaluating the importance of albedo feedback by estimating how much it would increase temperatures while thinking that temperature perturbations are only damped by those infrared photons emitted by the surface. But this albedo feedback would never, in reality, operate in the absence of the strong negative “tropospheric feedback.” So one gets a very skewed picture of the underlying dynamics, despite the fact that this is simply making a particular, unconventional, choice of reference response.
Those of you who have glanced at the paper linked to above will realize that by introducing the idea of the arbitrariness of the reference response, what I am really trying to do here is soften you up to the idea of redefining how we talk about water vapor feedback — by using a fixed tropospheric relative humidity, rather than fixed specific humidity, as the reference response. More about this in another post.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Isaac: I have seen a related issue of the arbitrariness of this definition of the reference response come up in discussions with systems (control) engineers in places like over on Anthony Watts’s blog. Some of them will argue vociferously that any net positive feedback leads to instability, despite my attempts to explain that as long as the positive feedback is not too large, its role is to magnify the no-feedback response but not to produce instability.
As near as I can understand it, if we wanted to adopt their way of looking at the system, then rather than talking about the Planck response as producing the “no-feedback” temperature change and going from there, we would instead look at things in terms of feedback on the original change in radiative imbalance due to a change in CO2 concentration (or whatever). In this picture, the Planck response itself is considered a negative feedback because it says that as the temperature rises, the radiative imbalance decreases. (In fact, I noticed that in his textbook, Dennis Hartmann chooses this point-of-view and thus refers to the Planck response as the “Stefan-Boltzmann feedback”.)
And, then using this terminology, the statement of the state that the climate system is believed to be in is one where the net feedback (including the “Stefan-Boltzmann feedback”) is negative, but less negative than the Stefan-Boltzmann feedback alone.
Joel, I would just be careful to distinguish between the issue of what names we give specific terms in our equations (what you are talking about, I think) and rearranging the equations and then giving the resulting terms new names (what I am doing above when talking about “tropospheric feedback” for example).
Isaac,
The following sentences from Held and Shell seem to be crucial.
(In order they appear in the text.)
i) “Being aware of this arbitrariness can be important; while the behavior of the system is unchanged by how one chooses to analyze it, different choices can simplify or complicate one’s conceptual picture of the processes controlling the climate response.”
ii) “There is little correlation across the models between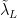 and
and 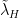 , suggesting that the remaining scatter has different sources in these different feedback terms, unlike the situation in the traditional formulation.”
, suggesting that the remaining scatter has different sources in these different feedback terms, unlike the situation in the traditional formulation.”
iii) “Whether this approach simplifies the analysis of observations of climate change will depend on whether observed relative humidity changes remain small, especially in the tropical upper troposphere, where these changes would have the largest effect on the troposphere’s radiative balance (Soden et al. 2005).”
iv) “A drawback is that one loses contact between the reference, “no feedback”, sensitivity and the simplest textbook estimate based on Stefan-Boltzmann.”
The last of these (iv) expresses a sentimental attachment that I don’t share. I believe many factors contribute to the correspondence with this simplified view and I wonder whether this owes much to happenstance. It is more important to me that the reliance of (Planck response at constant specific humidity) on radiative transfer (part of the puzzle that is well understood) means that we have some certainty in its value, as is expressed by its narrow range in the simulators. It gives us a firm peg in the ground against which to construct the dimensionless feedback factors. This is just as true of
(Planck response at constant specific humidity) on radiative transfer (part of the puzzle that is well understood) means that we have some certainty in its value, as is expressed by its narrow range in the simulators. It gives us a firm peg in the ground against which to construct the dimensionless feedback factors. This is just as true of  (response at constant relative humidity) and the paper reports that its spread in the models is just as narrow (in fact marginally narrower).
(response at constant relative humidity) and the paper reports that its spread in the models is just as narrow (in fact marginally narrower).
The second sentence (ii) seems to report and echo (Ingram (2010)) an important finding. This seems to be akin to having found a more orthogonal basis for the problem at hand, a choice of vectors whereby the projection of the models onto them express less covariance. (Here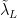 and
and 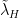 are the inferred model feedbacks for lapse rate and humidity under a scheme assuming fixed relative humidity as a basis vector as opposed to fixed specific humidity.) Your paper reports that the over all spread in three coefficients (temperature, humidity, lapse rate) is halved by this change of basis from constant specific humidity to constant relative humidity. Whether this expresses a truth that fluctuations in humidity are compensated for by a determined fluctuation in lapse rate, or merely a model happenstance is an interesting question. If the first is true the new basis characterizes the situation well, if the second is true it hides an issue that would best not be hidden.
are the inferred model feedbacks for lapse rate and humidity under a scheme assuming fixed relative humidity as a basis vector as opposed to fixed specific humidity.) Your paper reports that the over all spread in three coefficients (temperature, humidity, lapse rate) is halved by this change of basis from constant specific humidity to constant relative humidity. Whether this expresses a truth that fluctuations in humidity are compensated for by a determined fluctuation in lapse rate, or merely a model happenstance is an interesting question. If the first is true the new basis characterizes the situation well, if the second is true it hides an issue that would best not be hidden.
This feeds into the third sentence (iii). The new basis seems to be well adapted to the problem of characterizing the simulators, seeing where they materially differ from each other and best expressing the nature of their differences. The differences are minimized in terms of these three coefficients but if the observations come to disagree with near constant relative humidity is this new basis still to be preferred. If the lapse rate is in reality strongly determined by the humidity in the way that this choice of basis highlights in the models then the answer seems to be that it is to be preferred. Could it not then be that the models would be expressing a common, quite tightly defined bias in radiative transfer well expressed just in terms of a bias in humidity?
The first sentence (i) informs us that we can make intelligent choices as to which basis best characterizes the problem in light of the question being addressed. I suspect that there is a reluctance to the adoption of alternatives. I think I have expressed why I think sentences (iv) and (ii) indicate that nothing useful is lost under the alternative basis and if the apparent relationship between humidity and lapse expresses a truth then much could be gained.
(I would like to see the new kernel for a change in temperature at constant relative humidity. Hopefully I could better understand how varying the lapse rate at constant relative humidity effects radiative transfer. I have presumed throughout that under constant RH the kernel will have less amplitude in the upper troposphere thereby reducing the effect of varying the lapse rate. FWIW I think your basis makes the problem easier to understand and the application of kernels more intuitive, precisely because my struggle to continually bear in mind the lapse rate/humidity compensation is removed. I think that your papers with Soden 2006/2008 would be more intuitive and clearer under constant RH but I guess that they would not then have addressed the expectations of the readership. My only real worry is whether the consistency of lapse rate/humidity compensation demonstrated by the simulators expresses a truth.)
Many Thanks
Alex
Alex, I think you understand what I am saying very well. And I agree that if in reality relative humidity does change enough to impact the global energy budget as temperatures warm, the advantages of the feedback framework described in the Held and Shell paper will be reduced.
Thanks Isaac,
There is something related that always bothers me.
A reduction in the magnitude of the lapse rate with warming implies that the upper troposhpere must warm more rapdily than the surface, which I find odd.
Yet if I think about this not in terms of altitude but of pressure the excess warming may be transformed away.
I believe to the first order, tropospheric volumes scale in proportion to the absolute temperature. Providing the reciprocal of the lapse rate doesn’t scale any faster than the absolute temperature that excess warming would not occur in the pressure point of view. If the product of the lapse rate and the temperature was more or less a constant, the temperature difference between the surface and each pressure level would remain the same, to the first order.
In terms of radiative transfer it seems to be how far up the atmosphere a layer is in terms of the mass above and below (e.g. pressure) not the altitude, that matters. So I would use pressure when trying to think about radiation, in which case, to the first order, the troposphere would be warming evenly throughout. That would simply seem less odd to me.
If it turns out the lapse rate varies more strongly than that, either in the real world or in the simulators, it will go back to seeming somewhat odd. That doesn’t really matter, the main point being that the excess warming in terms of altitude might be much reduced or reversed in the pressure point of view.
I would be very pleased to know the answer.
Alex
The term that you are referring to is small compared to the change in moist adiabatic lapse rate with increasing temperature — the picture looks more or less the same whether you look at it in height or pressure coordinates.
Isaac,
Thanks again regarding lapse rate and pressure.
I will have to confess that I find myself struggling with some aspects of the papers, Soden & Held 2006 & 2008). Some of my difficulties are proving to be an impediment to a workable understanding of the origin of the negative correlation between and
and 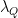 and why it is absent between
and why it is absent between 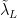 and
and 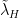 .
.
Before I go further, I ask whether the origin of this correlation is an important point that you intend to explain as your presentation unfolds. If so, you could confirm that much and delete what follows.
At the risk of seeeming a bit slow in the head, I have found the nature of the water vapour kernel a bit elusive. My clue to a better understanding and an explanation of why I, (and perhaps others) might find it confusing is highlighted by the units for the kernal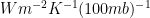 and why these are the same for the temperature kernel.
and why these are the same for the temperature kernel.
There seem to be two different interpretations of temperature in the demoninator. In the latter case (call it kernel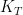 ) it is a thermometer temperature, in the other case (call it
) it is a thermometer temperature, in the other case (call it 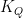 ) it is equivalent to the change in temperature necessary to produce the required change in water vapour at constant relative humidity. Is that correct?
) it is equivalent to the change in temperature necessary to produce the required change in water vapour at constant relative humidity. Is that correct?
If so, may I say that these papers are complex and it is a point that I didn’t fully appreciate in SH2006 but this is my interpretation of Section 4 of SH2008.
That being the case, a tendency for the simulators to track close to constant relative humidity would result in an equivalent water vapour temperature that already includes the effect of any change in the lapse rate. More generally, no matter how the water vapour responds to temperature it is the actual temperature, the combined surface and lapse rate change, that affects the water vapour content and gives rise to an equivalent change in temperature that already includes a lapse rate component and hence, in order to balance, the will include a compensation which shows up as a negative correlation with
will include a compensation which shows up as a negative correlation with 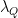 unless
unless 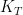 is replaced with some
is replaced with some  that already includes the appropriate water vapour effect.
that already includes the appropriate water vapour effect.
It so happens that the simulators track constant relative humidity but if they didn’t but clustered around a different track, and one that could be expressed as a ratio between real and water vapour equivalent temperatures, that could lead to a different choice for for model comparison that reflected the average track of the ensemble and still present the results in a form where the correlation was minimised.
for model comparison that reflected the average track of the ensemble and still present the results in a form where the correlation was minimised.
In the spirit of maintaining the arbitrariness, I am trying to see all this in a way that prevents the lack of correlation between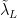 and
and 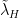 appearing to be meaningful.
appearing to be meaningful.
I welcome any comments, especially if I am missing the point. I won’t mind being wrong given the challenge I think those papers, and the one in question here, present.
Alex
Alex,
Brian and I decided to normalize the “water vapor kernel” in this way so that it would be easily compared to the temperature kernel in the case in which relative humidity is unchanged. This is a convention, and nothing in the results of the feedback analysis depends on this normalization. (This choice does make it easier to talk about which parts of the atmosphere contribute most to the traditional water vapor feedback, when relative humidity is unchanged — this is a good topic for another post.)
If models did decrease the relative humidity a lot as they warm,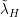 would be large and negative. If, for some reason, specific humidity was conserved, I think you would then expect correlation between
would be large and negative. If, for some reason, specific humidity was conserved, I think you would then expect correlation between  and
and 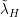 across the models — the models that warmed more in the tropical upper troposphere would need a larger reduction in relative humidity to maintain the same specific humidity. You can presumably find a basis after the fact in which the different feedbacks are uncorrelated across an ensemble of models, but I don’t think any particular choice of variables will work in general.
across the models — the models that warmed more in the tropical upper troposphere would need a larger reduction in relative humidity to maintain the same specific humidity. You can presumably find a basis after the fact in which the different feedbacks are uncorrelated across an ensemble of models, but I don’t think any particular choice of variables will work in general.
Isaac,
Thanks for the link to your paper- it is extremely elegant in its thought and outline, and seems like it can have some degree of practical application, especially if global relative humidity changes tend to be small. I had two questions on the paper (sorry if this is premature as you prepare your next blog post, or if I’m missing something basic, as I’m tired)-
1) The constant relative humidity property is obeyed to first order on a global scale, but it is not necessarily true on a local scale. In perturbing a model by 1 K and seeing how the OLR increases w constant relative humidity, it seems to me that there is a loss of information on the geographic structure of your “no-feedback, RH conserved” climate sensitivity. This would then be compensated for by large regional variation in the feedback term ). This would be true of regional variations in any reference system, but it seems less artificial in the traditional view, where it’s just the Planck increase in radiant flux reacting rather than the dynamics that constrain relative humidity. But I’m also not sure if it is interesting, since the no-feedback sensitivity is not a property of the real Earth system.
). This would be true of regional variations in any reference system, but it seems less artificial in the traditional view, where it’s just the Planck increase in radiant flux reacting rather than the dynamics that constrain relative humidity. But I’m also not sure if it is interesting, since the no-feedback sensitivity is not a property of the real Earth system.
2) Would you view a worthwhile extension of your paper to include non-linearity in the feedback terms (and reference system itself) with the climate state (for larger changes)? It’s not much for small changes, but the behavior of the OLR vs. T curve is interesting in shedding light on broader planetary science questions, like the origin of the runaway greenhouse. This is sometimes viewed as one possible bifurcation if exceeds one, but in your reference system, it’s the numerator in Equation 14 of your paper that seems to increase rapidly with temperature.
exceeds one, but in your reference system, it’s the numerator in Equation 14 of your paper that seems to increase rapidly with temperature.
Joel- For people not initiated in how feedback terminology works in climate, it might be convenient to illustrate this from the perspective of the dependence between OLR and surface T (for example, in this post I did).
1) There are large regional variations in a lot of aspects of modeled climate responses, clouds especially but also relative humidity. The global mean energy budget is just a starting point.
2) In these posts I have been emphasizing simple linear pictures of climate responses to small perturbations, because I believe that climate responses are, in fact, linear for small perturbations, and this is not widely enough appreciated. So I may be giving the false impression that nonlinearities that develop as perturbations increase in size are not important — a lot of the interesting dynamical issues relate to these nonlinearities.
Isaac,
I feel like I am missing something from a layperson’s standpoint. If you fix relative humidity you eliminate the traditional large positive water vapor feedback as clearly shown in your Figure 1. OK.
But since the standard terminology of the “no-feedback response” to a doubling of CO2 includes the physically necessary Stefan-Boltzmann or Planck responses, by changing the decomposition as you propose you are going to radically alter the magnitude of the “no-feedback response”. Instead of being 1.2K it’s going to be what, double that? Thus I feel like this is going to take A LOT of explanation to laypeople and particularly skeptical laypeople that it is not a fudge (which it is clearly not). It’s going to be said that terminology is being changed to eliminate the need for “strong positive feedbacks” as has always been claimed to be the case.
If my last paragraph seems harsh I don’t intend for it to. Perhaps my projection of the consequences of this terminology change is too strong.
Final note – I believe my comment is unconnected to Joel’s above, though obviously he reads some of the same blogs I do.
The reference response in our calculation is increased by a factor of about 1.8 (1.77 to be precise) by fixing relative rather than specific humidity.
If there is a good scientific reason to modify your feedback terminology then you should do it, irrespective of the reactions of “skeptical laypeople” or anyone else.