Posted on May 16th, 2013 in Isaac Held's Blog
Schematic of the response of tropical rainfall to high latitude warming in one hemisphere and cooling in the other or, equivalently, to a cross-equatorial heat flux in the ocean. From Kang et al 2009.
When discussing the response of the distribution of precipitation around the world to increasing CO2 or other forcing agents, I think you can make the case for the following three basic ingredients:
- the tendency for regions in which there is moisture convergence to get wetter and regions in which there is moisture divergence to get drier (“wet get wetter and dry get drier”) in response to warming (due to increases in water vapor in the lower troposphere — post #13);
- the tendency for the subtropical dry zones and the mid-latitude storm tracks to move polewards with warming;
- the tendency for the tropical rainbelts to move towards the hemisphere that warms more.
There are other important elements we could add to this set, especially if one focuses on particular regions — for example, changes in ENSO variability would affect rainfall in the tropics and over North America in important ways . But I think a subset of these three basic ingredients, in some combination, are important nearly everywhere. I want to focus here on 3) the effect on tropical rain belts of changing interhemispheric gradients.
My exposure to this issue started some time ago listening to Suki Manabe discussing early coupled atmosphere-ocean model simulations in which the latitude of the Pacific intertropical convergence zone (ITCZ) was sensitive to the cloud cover in midlatitudes of the Southern Hemisphere — these were the days in which cloud cover was prescribed in the models so it was easy to manipulate. By increasing the cloud cover in the South, well away from the tropical rainbelts themselves, one could move the ITCZ from south of the equator to north of the equator (where it is in reality).
In the late 80’s a flurry of work on Sahel rainfall and particularly the severe drought in the preceding decade, starting with Folland et al 1986, argued that much of the decadal variability in the Sahel is tied to the differential warming of the hemispheres. Relatively cool Northern Hemisphere, as in the 70’s, results in less Sahel rainfall, thinking of the Sahel as marking the northernmost extension of the ITCZ, or monsoonal rainfall, over Africa, which retreats due to the pull of the differential cooling of the Northern with respect to the Southern Hemisphere. While there are other things going on in the Sahel, most recent research supports this picture of variations in interhemispheric temperature gradients, whether produced by variability in Atlantic overturning or aerosol forcing, as being a big part of the Sahel drought picture. I talk about this here, although that page is a bit dated.
John Chiang and collaborators have emphasized the importance of this mechanism for paleoclimate as well as higher frequency climate variations in a series of papers, see this recent review (Chiang and Friedman, 2012). Another paper that affected my own work on this issue was that of Broccoli et al 2006, which helped shift the picture of the underlying dynamics from one focused on surface energy balances and changes in tropical ocean temperatures to one focused on the requirements of atmospheric energy balance. Two former students of mine, Sarah Kang and Dargan Frierson, have picked up on this energy balance perspective in more recent work, starting with Kang et al 2008.
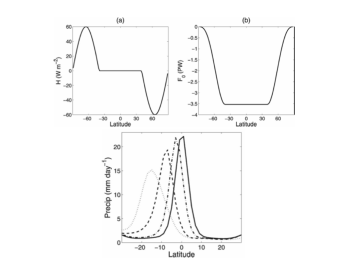 Sarah has focused on a setup in which one takes an atmospheric model of the type used for climate simulations and couples it to a “slab ocean” of uniform depth with no ocean currents, which just provides some heat capacity and a saturated surface. Starting with the case in which there is no heat flux through the bottom of the slab ocean, the resulting climate is independent of longitude and symmetric about the equator, with most tropical precipitation confined to a sharp ITCZ located over the equator (the solid line in the lower panel). The model determines its own surface temperature, and the energy flowing into the slab will be zero everywhere if you average long enough. (One of the nice things about this setup is that, unlike models in which surface temperatures are prescribed, you never have to worry about generating a double ITCZ.) Heat is then added poleward of 40N in one hemisphere and the same amount is removed from the other hemisphere (as pictured in the upper left panel.) . This is equivalent to prescribing a cross-equatorial heat flux in the ocean underneath the slab (upper right). No heat is being input or extracted equatorward of 40 degrees. After the model equilibrates, the ITCZ has moved into the warmed hemisphere. The larger the heating, the larger the displacement of the ITCZ. The lower panel shows the precipitation from simulations in which the peak in the imposed subpolar heating/cooling is 10, 20 and 40 W/m2.
Sarah has focused on a setup in which one takes an atmospheric model of the type used for climate simulations and couples it to a “slab ocean” of uniform depth with no ocean currents, which just provides some heat capacity and a saturated surface. Starting with the case in which there is no heat flux through the bottom of the slab ocean, the resulting climate is independent of longitude and symmetric about the equator, with most tropical precipitation confined to a sharp ITCZ located over the equator (the solid line in the lower panel). The model determines its own surface temperature, and the energy flowing into the slab will be zero everywhere if you average long enough. (One of the nice things about this setup is that, unlike models in which surface temperatures are prescribed, you never have to worry about generating a double ITCZ.) Heat is then added poleward of 40N in one hemisphere and the same amount is removed from the other hemisphere (as pictured in the upper left panel.) . This is equivalent to prescribing a cross-equatorial heat flux in the ocean underneath the slab (upper right). No heat is being input or extracted equatorward of 40 degrees. After the model equilibrates, the ITCZ has moved into the warmed hemisphere. The larger the heating, the larger the displacement of the ITCZ. The lower panel shows the precipitation from simulations in which the peak in the imposed subpolar heating/cooling is 10, 20 and 40 W/m2.
One way of thinking about this is to focus on how the surface temperatures in the tropics are affected by the extratropical heat sources/sinks, assuming that the ITCZ will follow the warmest surface temperatures. But I prefer a perspective based on the atmospheric energy budget, as in the papers by Broccoli et al and Kang et al linked to above.
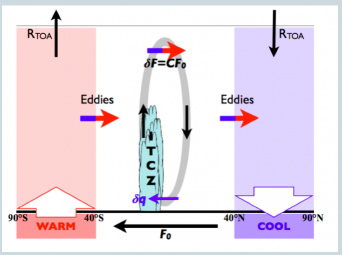
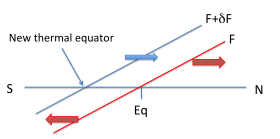
Before the system is disturbed, the northward heat flux F in the atmosphere is zero at the equator and has some slope in latitude as pictured below. The Hadley cells, symmetric about the equator, have poleward flow in the upper troposphere and equatorward flow near the surface, with rising motion mostly confined to the ITCZ. These cells transport energy in the direction of their upper tropospheric flow. In response to the high latitude heating and cooling, the atmosphere tries to resist the resulting interhemispheric asymmetry by transporting energy across the equator from the heated to the cooled hemisphere. In this setup, you can equivalently talk about how much of the prescribed oceanic flux is compensated by an atmospheric flux in the opposite direction. In the schematic at the top of the post, the fraction of the flux that is compensated is denoted by C. Putting aside how C is determined, we can estimate the new latitude of the “energy flux equator” where the atmospheric flux vanishes. (See sketch below.) If simple Hadley cells continue to dominate the horizontal energy fluxes in the tropics, with most of the rising motion in a sharp ITCZ, then the ITCZ will need to be close to this energy flux equator so that energy flows away from this latitude in both directions.
But how do you estimate C? Start by ignoring any responses in clouds. Part of the input of energy into the warmed hemisphere is balanced more or less locally by an increase in the energy radiated away to space and the rest is transported to low latitudes. I picture the transport as a diffusive process (post #37), with a diffusivity that weakens as one approaches the tropics, where the mean meridional circulation (the Hadley cell) takes over a lot of the energy transport. The subtropical heating/cooling by midlatitude storms creates a problem because the tropical atmosphere can’t sustain large horizontal temperature gradients. If the change in the net radiation at the top of the atmosphere is primarily a function of tropospheric temperature (ie if clouds don’t change), then the changes in this net radiation have to be very uniform with latitude across the tropics. So the key from this perspective is the extent to which the eddy diffusive-like fluxes in midlatitudes manage to extract or input energy into the subtropics of each hemisphere, which the circulation must then redistribute.
As discussed in the Kang et a papers linked to above, if we either fix clouds in the GCM or use an idealized moist GCM with no clouds, this degree of compensation at the equator, C, seems to be of the order of 25-40%, a value you can get from a simple diffusive model with the diffusivity tuned to the atmospheric fluxes in the control climate. If you use the standard AM2 model that was used in our contribution to the CMIP3/AR4 database, you get something like 80%, but this number can be changed by manipulating the closure scheme for moist convection. It’s not the convection per se that matters, but the effect of the convection scheme on the cloud feedbacks — the response of clouds to this extratropical heating/cooling perturbation and the effect of these changes on the top-of-atmosphere (TOA) balance. It is still the TOA that matters here, because the net surface fluxes are prescribed — one can only change the net atmospheric poleward fluxes if the TOA fluxes change. (It is this emphasis on the TOA fluxes that distinguishes this perspective from those focusing on surface temperatures.)
There are two distinct kinds of cloud feedbacks that come into play. First, there can be changes in clouds in the high latitude regions which are directly being heated or cooled. These modify the heating/cooling that the atmosphere feels, so they effectively renormalize the forcing. But in addition, once the tropical circulation is modified clouds in the tropics will react to these changes in circulation to alter the energy transports needed to homogenize the tropical temperatures. For example, the strength of the subsidence increases in the tropics and subtropics of the cooled hemisphere, which might result in an increase in low level cloudiness (due to the suppression of vertical mixing of vapor into the upper troposphere)– a positive feedback on the initial cooling. (The movement of the ITCZ would also directly generate changes in long and shortwave fluxes at the TOA, but these tend to cancel — the effects of shallow clouds are often dominant.) So this is a hard problem to get right quantitatively, as are all cloud-related issues it seems. But the qualitative effect is clear.
This mechanism is important when thinking about the tropics during past glacial periods, given the large cooling associated with Northern ice sheets. It is important for the response to aerosol forcing that preferentially cools the Northern Hemisphere. It is important for the response to variations in the Atlantic meridional overturning, which directly modifies the cross-equatorial ocean flux. And it can be important for understanding the mean climatology, as indicated by the reference above to Suki Manabe’s early experience with coupled atmosphere-ocean models (see also Hwang and Frierson, 2013 and Marshall et al 2013).
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Great post. I wonder about the role of the tropical cloud feedbacks that result from the ITCZ shift itself and it’s feedback on cross-equatorial heat transport. (i.e. if you shift the ITCZ Northward, how do the resulting cloud feedbacks influence the hemispheric contrast of net radiation at the TOA). I think the statement in the post that the longwave and shortwave mostly cancel is true but not completely true. I think we have evidence from models and observations that the inter-annual variability of ITCZ location leads to TOA radiative imbalances that further heat the warm hemisphere (the hemisphere that the ITCZ has shifted into). The reason being, if you shift the ITCZ North, the clouds reflect more shortwave in that hemisphere (less absorbed shortwave) and there is less OLR emitted (energy gain) but the longwave change appears to be bigger in magnitude than that in the shortwave, so the net change is to heat the Northern tropics -> positive feedback on the initial shift. Does any have any thoughts as to why one might expect the longwave change to be larger than the shortwave change and if this is robust across different models and/or the observations?
It doesn’t take much imbalance between the shortwave and longwave effects of the deep convection for the net to be important. but what I am confused about is how this affects the ITCZ displacement if it rides with the ITCZ itself. The interhemispheric radiative forcing difference seems like a useful measure when considering forcing away from the ITCZ itself, but it is not clear to me that it is the relevant metric if it contains a large part that follows the ITCZ.
I agree with you; the radiative response to an ITCZ shift most likely isn’t the cause of the shift but can act as a feedback on the shift itself. I think we’re gathering evidence that it acts as a positive feedback which begs the question of what stabilizes the system (brings the ITCZ back to equilibrium position). I think the seasonal cycle of insolation and thus the seasonal ITCZ migration is the stabilizing influence.
Aaron, if one focuses on the cross-equatorial energy transport, then the changes in TOA flux associated with the ITCZ movement are a part of the story. But suppose that the system is really just trying to reach a consistent energy balance on both sides of the ITCZ (thinking of the ITCZ as a wall). Then it is not clear to me that the TOA signal of the ITCZ, which moves with the ITCZ, will make much of a difference. I would be reluctant to accept that the seasonal cycle is needed to stabilize the ITCZ position since it seems quite well behaved in aquaplanet models with no seasonal cycle.
Not that I am entirely clear on the simplest starting point for this problem. Even in Sarah’s idealized model the tropical rainfall broadens a lot as it moves off the equator, so the idealization of an ITCZ acting as a wall at the point of vanishing poleward energy flux is not very compelling. This one of the reasons why we moved away from thinking of the ITCZ latitude as something to be explained (I didn’t get to this in this post) and instead tried to think in terms of a picture dependent on constraining the gross moist stability (the ratio of energy transport to mass transport in the Hadley cell).
Very interesting.
Marcel LeRoux didn’t receive a lot of credit for his ideas, probably because he didn’t offer many physical equations to substantiate his observations. But one of his ideas was the meandering of the ITCZ driven by the colder pole. A sterling example was the Holocene Climatic Optimum. During the HCO, Northern summers received disproportionately higher amounts of insolation, which contrasts with present times in which Southern summers receive disproportionately higher amounts of insolation. The result, which is consistent with the colder, denser hemisphere displacing the ITCZ – further north during the Northern HCO summers and further south during current Southern summers.
There is a great tool to view the insolation, forecast.uchicago.edu/Projects/orbit.html
Contrast years 2013 and -6000.
This is not strictly analogous to CO2 driven warming. The insolation varied by close to 50w/m^2 ( total radiative forcing would have been less of course, but still greater than what we expect from CO2 doubling ). But to the extent that CO2 might displace the ITCZ, one would consider whether seasonal skew meant disproportionately warmer winters than summers, and the extent of Arctic amplification.
That the Climatic Optimum was primarily driven by changes in insolation (more insolation in Northern summer and less in Northern winter) is the standard hypothesis and has been used repeatedly as a test of climate models, as one can see by searching on the Paleoclimate Modelling Intercomparison Project. Modeling studies go back at least to John Kutzbach’s work in the early 80’s, with an emphasis on the African humid period, one focus being on whether vegetation feedbacks are needed to create a model that is as humid as Northern Africa was during this period.
Hi Isaac
It is not the topic but I’m searching the reasons of the subsidence in the Hadley cells.
One of the usually invoked reasons is the radiative cooling but I don’t understand why this radiative cooling should affect only the air parcels of Hadley cell.
To fall an air parcel must be cooler than the ambiant air, or is it the ambiant air that falls?
And why?
Could you give me an explanation, please?
Since the post concerns Hadley cells, this is close enough.
Radiative cooling is present nearly everywhere in the troposphere. The distinctive aspect of the tropics is that horizontal temperature gradients are small enough that horizontal motions bringing warmer air in from somewhere else cannot help balance this cooling, unlike higher latitudes. So one is left with two possibilities: vertical motion — that is, adiabatic warming due to subsidence — or latent heat release in convection. You get a large scale circulation in the tropics by concentrating the convection in a certain area, like the ITCZ, with net upward motion in this region of sustained convection and subsidence elsewhere. The area in which the latent heating occurs is relatively small, so most of the tropics is subsiding. In an idealized Hadley circulation the subsiding air will be denser than the air in the regions of upward motion at the same pressure level, on average, in order to generate the kinetic energy of the circulation. i don’t think in terms of “ambient air” in this context. The atmosphere is pretty complicated, and you can try to understand it starting from different perspectives, but this is the picture of the tropics that I start with.
Dr Held –
I hope you’ll consider this comment, as I began following your ideas here by tracking potential temperature (PT), and ended at meteor’s question.
I’m considering why the ITCZ should be a persistent structure.
Working backwards from your 3rd diagram: You show energy outflows, so this applies to ITCZ top air (with highest initial PT). You indicate equal flows, so mass- and energy-flow arguments are interchangeable. Converging bottom air progressively picks up PT. At the “heat equator”, N & S PT will be equal. An ITCZ elsewhere should form a cold front, which will naturally migrate to correct this. As air PT is equal, mass inflows should also match.
This provides a credible position for the ITCZ bottom (and so top), and equal inflows.
But this doesn’t explain equal outflows, which I need for top stability. “Must match inflows” is unpersuasive.
The ITCZ establishes a lapse-rate (LR) profile averaging around 6°/km, where outside it is the DALR of 10, apparently preventing subsidence. High-PT air flowing poleward from the ITCZ will cool by radiation (OLR), but the corresponding bottom air (inflowing) is also cooler. The Hadley subsidence should be an extended region of fairly constant LR profile matching that of the ITCZ. This region must be strongly ordered, similar to upward heat conduction through a descending solid slab; ie countercurrent heat and mass flow.
If that passes inspection:
Cooling of a column of Hadley subsidence depends (as you say) on the presence of IR heat-absorbing components (“GHG.s”). Back-of-envelope suggests that any slice of that column receives net radiant heat from below, varying roughly as the square of local LR and inversely as GHG “concentration”. The strong LR dependence should act to minimise local LR until it permits subsidence, which will reduce upward heat-transfer.
This scheme provides an orderly route for top air at high PT to descend and join the low(er) PT bottom air inflow, and also flow-resistance tending to equalise ITCZ top outflow (mass, so heat).
As the control is the top/bottom PT difference, this mechanism suggests that behaviour may be relatively insensitive to amount or nature of GHG.s.
This presents the ITCZ and Hadley circulation as a self-organising heat engine, possibly most affected by GHG.s via their indirect effect on extratropical heating. Has the model you describe been used for this?
The inverse dependence on GHG.s suggests this mechanism is inoperative at high concentration. Venus’ upper troposphere apparently shows near-classical DALR, consistent with this. My approximation naturally fails at zero GHG, so this model is inadequate to estimate the true GHG sensitivity.
The ITCZ position appears to be an available metric for heat flow anomalies (such as warm/cold meridional currents) globally.
You seem to be arguing for the boundary between the northern and southern branches of the Hadley cell being located at the warmest surface temperatures, an idea that is very intuitive and made more precise by Previ and Plumb 2007 who talk about the maximum in moist static energy (which is going to be close to the maximum in temperature over the oceans). But this does not say anything about why the SST maximum is where it is — it could adjust to the hadley cell structure rather than the other way around potentially. You also don’t seem to be focusing enough, if I understand you correctly, on the need to maintain a very uniform horizontal temperature field within the Hadley cell and above the boundary layer. I also don’t share your concern about matching mass fluxes in the upper level branches to the mass fluxes in the lower branches, which just seems like mass conservation. The Previ-Plumb paper linked to above provides one entry point into the literature on these kinds issues.