Posted on July 16th, 2013 in Isaac Held's Blog
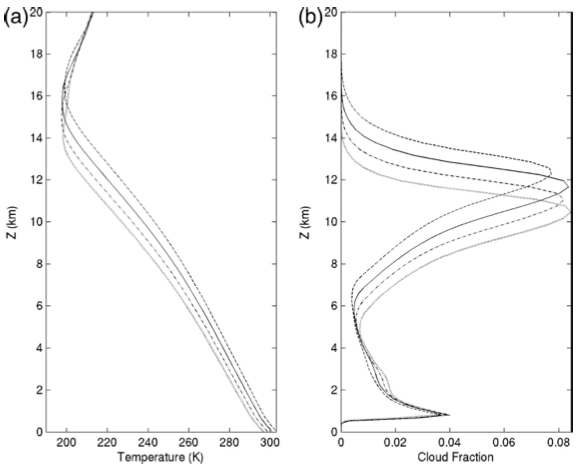 The response of a 1km non-rotating doubly periodic model of radiative-convective equilibrium to an increase in surface temperature, in increments of 2K. Left: temperature, showing a moist-adiabatic response; Right: fraction of area with cloud at each height, showing an upward displacement of upper tropospheric clouds. From Kuang and Hartmann 2007.
The response of a 1km non-rotating doubly periodic model of radiative-convective equilibrium to an increase in surface temperature, in increments of 2K. Left: temperature, showing a moist-adiabatic response; Right: fraction of area with cloud at each height, showing an upward displacement of upper tropospheric clouds. From Kuang and Hartmann 2007.
The presence of cirrus clouds in the tropics warms the troposphere because infrared radiation is emitted to space from their relatively cold surfaces rather than the warmer temperatures below the clouds. The response of these clouds can be important as feedbacks to climate change. A reduction in the area covered by these high clouds would be a negative feedback to warming. [7/25/13: Several readers have pointed out that a reduction in the areas of high cloud cover would be a negative infrared feedback but a positive shortwave feedback and that the net effect could go either way.] An increase in the average height of these clouds with warming, resulting in a colder surface than would be the case if this height did not increase, would be a positive feedback. It is the latter that I want to discuss here. GCMs have shown a positive feedback due to increasing height of tropical cirrus since the inception of global modeling (e.g., Wetherald and Manabe, 1980). This is probably the most robust cloud feedback in GCMs over the years and is one reason that the total cloud feedbacks in GCMs tend to be positive. This increase in cloud top height has, in addition, a clear theoretical foundation, formulated as the FAT (Fixed Anvil Temperature) hypothesis by Hartmann and Larson, 2002.
The FAT hypothesis argues that the temperature of these tropical cloud tops should remain at fixed temperature (to a first approximation) as the climate warms. The argument depends on the relative humidity remaining more or less unchanged in the tropical upper troposphere and on basic radiative transfer. The key aspects of radiative transfer relevant to FAT are discussed elegantly by Ingram 2010.
Most radiatively active cirrus clouds in the tropics are generated by the detrainment from deep convective clouds, starting out as the anvils of thunderstorms, thinning as they spread horizontally and evaporating as they subside and warm. Their characteristic height is determined by the height at which the strongest outflows from convective updrafts occur. What determines this outflow height?
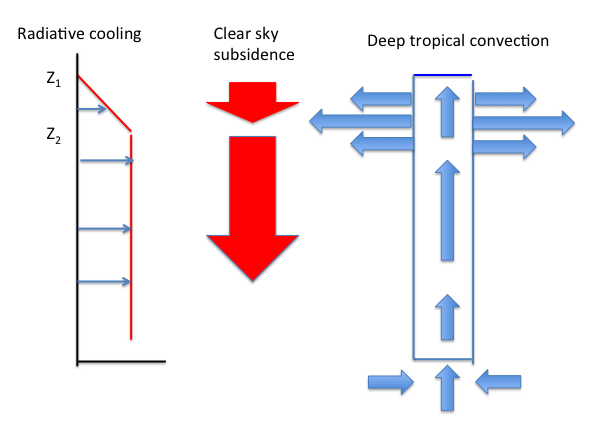
The temperature profile in the tropics is close to a moist adiabat set by the deep convection that occupies a small fraction of the area. This moist adabat is efficiently communicated to the rest of tropics and sets the temperature profile in non-convecting areas as well. When air tries to descend in the clear regions, to compensate for the upward mass flux in the deep convective cores, its temperature will try to follow a dry adiabat, but these temperatures are too warm to be consistent with the moist adiabat set by the convection, and it is the radiative cooling that allows for a consistent picture, with the magnitude of cooling setting the rate of descent of air away from the convection. Specifically, the subsidence rate is proportional to , where
is the radiative cooling and
is a measure of the dry stability of the air column, the departure of the temperature profile from the dry adiabat.
So the vertical structure of the radiative cooling in the clear sky must be consistent with the vertical structure of the upward mass fluxes in the deep convective cores, since the compensating subsidence is constrained by this radiative cooling. Suppose that the radiative cooling is constant below the height Z2 and drops to 0 at the higher level Z1 (see sketch below). The rate of subsidence needed to balance this profile of cooling will have a similar vertical structure (ignoring structure in ). This increase in subsidence in the clear tropical regions, by conservation of mass, must be accompanied by a transfer of mass from the convective cores to the subsiding region. So the outflow from the cores will be concentrated where cooling decreases rapidly with height.
 Water vapor is responsible for most of the cooling of the tropical upper troposphere. Roughly speaking the height at which the cooling has a sharp vertical gradient is determined by the total amount of water above this height. Since the saturation vapor pressure is a function of temperature only, if the relative humidity is fixed the profile of water vapor pressure in the vertical is determined by the temperature, and the temperature at which this gradient occurs will tend to be fixed. Ingram, in the paper linked to above, provides a clear discussion of the assumptions required to get the result that the infrared cooling rate is a function of temperature only. Besides fixed relative humidity (or more generally, relative humidity that is a function of temperature), the key assumption is that infrared absorbers/emitters other than water vapor, including the surface, can be ignored in computing the cooling in this region. I won’t try to duplicate that analysis here.
Water vapor is responsible for most of the cooling of the tropical upper troposphere. Roughly speaking the height at which the cooling has a sharp vertical gradient is determined by the total amount of water above this height. Since the saturation vapor pressure is a function of temperature only, if the relative humidity is fixed the profile of water vapor pressure in the vertical is determined by the temperature, and the temperature at which this gradient occurs will tend to be fixed. Ingram, in the paper linked to above, provides a clear discussion of the assumptions required to get the result that the infrared cooling rate is a function of temperature only. Besides fixed relative humidity (or more generally, relative humidity that is a function of temperature), the key assumption is that infrared absorbers/emitters other than water vapor, including the surface, can be ignored in computing the cooling in this region. I won’t try to duplicate that analysis here.
This seems like a long argument with a lot of assumptions, but it is confirmed rather beautifully in high resolution cloud-resolving simulations in small domains. The figure at the top is from a high resolution (1km in the horizontal) model of non-rotating radiative-convective equilibrium of the sort discussed in posts #19 and 26. This kind of model allows us to directly simulate aspects of deep moist convection in the tropics. The domain is 64 x 64 km. (The small domain serves to avoid some of the issues related to spontaneous aggregation discussed briefly in #19.) A nice feature of this simulation is the relatively high vertical resolution compared to most other models of this type. The surface temperature is a prescribed boundary condition. The two plots above show the averaged temperature and cloud cover responses to warming of surface temperature. The warming on the left has the familiar structure of increasing amplitude with height consistent with a moist adiabat. And the clouds on the right clearly move upwards with warming.
But plotting the upper tropospheric cloud cover as a function of temperature rather than height, Kuang and Hartmann get the figure below (the modest changes in the magnitude of the cloud cover are removed from the plot by normalizing by the maximum value so as to focus on the vertical structure)
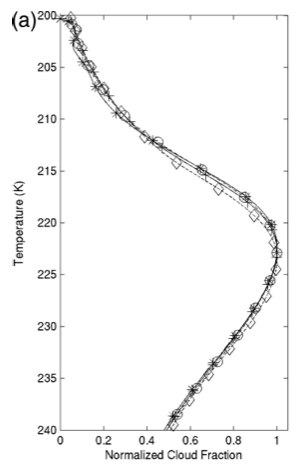 The theory works remarkably well. The change in the temperatures at the height of the maximum in the cloud cover is an order of magnitude smaller than the change in temperature at fixed height.
The theory works remarkably well. The change in the temperatures at the height of the maximum in the cloud cover is an order of magnitude smaller than the change in temperature at fixed height.
The arguments underlying this result are quite general and don’t depend on the changes in the extent of cloud cover or the spatial organization of the convection being negligible, as long as the relative humidity does not change much. So one should be able to see this FAT feedback in the interannual variability in the tropics, which is important since a lot of the satellite data that allows one to study this kind of thing is restricted to the last decade or so, which is not long enough to analyze trends usefully. Zelinka and Hartmann 2011 provide an extensive discussion of the observational picture based on analysis of internanual variability over the past decade. The result is very encouraging for the basic theory. They emphasize, however, that the way in which , the departure of the temperature profile from the dry adiabat, changes in interannual variability and in global warming might be sufficiently different to complicate inferences about subsidence profiles (
) and outflow temperatures from cooling rates
.
FAT cloud feedback is closely linked to water vapor feedback since it depends on relative humidity remaining relatively unchanged in the tropical upper troposphere (especially when plotted against temperature rather than height). Obviously, a lot rides on the response of relative humidity to warming.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Zelinka et al 2013 (J. Climate) decompose the cloud feedback into cloud fraction, cloud top pressure, and cloud optical depth feedbacks. Analogous to the feedback framework with a constant RH base state you introduced in Held and Shell 2012, could the cloud feedback (at least in the tropics) be conceived to consist of a FAT base state? Or is that implicitly already contained within the Held and Shell 2012 framework (since FAT depends on fixed RH)?
FAT is not included in the fixed RH reference that Karen and I used in the 2012 paper. Given the connection of FAT to fixed RH I think it would make sense to include it. But it is only in the tropics that one has this picture of how the level of the upper clouds is determined so it would not be very clean.
Thanks for the response. Technical difficulties of computing the feedbacks aside, I’m trying to think of what would be the most useful base state from which to conceptualize feedbacks operating, given what physical/dynamical responses we know to be robust in response to warming. In addition to constant RH and FAT, tropopause rise comes to mind (to which FAT is obviously linked).
Tropical expansion and polar amplification are other candidates, but how they would be quantitatively incorporated into the feedback framework seems especially shaky. Since they are less well constrained than say fixed RH or FAT, perhaps that’s going too far.
I wonder if this effect could introduce a bias in hurricane track algorithms when global climate is warming. They typically looked at fixed levels in the atmosphere.
The changes due to climate trends are presumably far too small to be of any relevance to hurricane strength algorithms from remote sensing, let alone track estimation.