Posted on September 9th, 2015 in Isaac Held's Blog
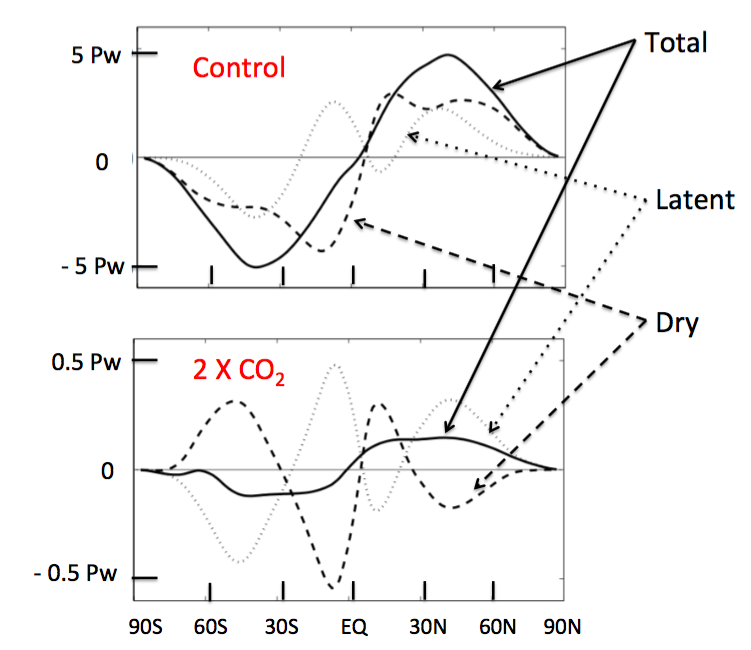
Upper panel: annual mean northward atmospheric energy transport as a function of latitude averaged over the control simulations in CMIP3. The total flux is shown as well as the decomposition into the latent flux and the dry static energy flux. Lower panel: Response of these fluxes to doubled CO2 (2 x CO2 minus control) in slab-ocean models with fixed oceanic heat transport. Fluxes in petawatts. Courtesy of Yen-Ting Hwang.
A warming atmosphere typically results in larger horizontal moisture transports. In addition to the implications for the hydrological cycle and oceanic salinity discussed in previous posts, this increased moisture transport also has implications for energy transport. If energy is used to evaporate water at point A and the vapor is transported to point B where it condenses, releasing the heat of condensation, energy has been transported from A to B. This latent heat transport is a large component of the total atmospheric energy transport. The thin dotted line in the top panel above is the northward latent heat transport averaged across the CMIP3 models. Outside of the tropics, eddies are mixing water vapor downgradient, resulting in a poleward transport. Close to the equator, the Hadley circulation dominates, with its equatorward flow near the surface that carries water vapor from the subtropics to the tropical rain belts (the compensating poleward flow near the tropopause carries very little water vapor in comparison). This tropical branch with equatorward vapor transport is clearer in the Southern Hemisphere in this plot, due I think to more continents and larger seasonal cycle of tropical rainfall in the north, producing less separation in the annual mean between the tropical and midlatitude rainbelts.
To get the total flux we add the remaining “dry” component, the flux of dry static energy, to this flux of latent energy. (I’ll refer to the flux of dry static energy as the “dry” flux here. Some background on atmospheric energy fluxes can be found on pages 50-51 here.) This dry flux (dashed line) is directed polewards everywhere but tends to have two maxima, one in low latitudes due to poleward flux in the Hadley cell, where this transport counteracts the latent heat flux — and another in midlatitudes dominated by the transport of sensible heat by midlatitude storms. The total atmospheric flux is very simple in contrast, varying smoothly in latitude and directed from equator to pole in each hemisphere, with a midlatitude maximum. The sense you get is that the total flux is a simpler object to think about than its components. I am going to focus on the extratropical part of these fluxes in the following.
In global warming simulations, the extratropical poleward latent flux increases, more or less as expected from an assumption of fixed relative humidity and fixed wind fields. The total poleward flux also increases, but the increase is smaller than the increase in latent flux. Without going into the details of how the response of the total flux might be controlled, it is evidently constrained in ways that the latent and sensible fluxes individually are not, so it cannot keep up with the increasing latent flux. The upshot is that the poleward dry flux outside of the tropics decreases with warming. The lower panel shows the response of “slab ocean” models in the CMIP3 archive to a doubling of CO2. (Hwang et al 2011 correct some errors in a similar plot in Held and Soden 2006. This plot is slightly different from the figure in Hwang et al. where the individual model responses are divided by their global mean surface warming. I thank Yen-Ting Hwang for redrawing this figure for this post.) In these slab ocean models the atmosphere is coupled to a shallow stagnant layer of water. Prescribed fluxes of heat into or out of the lower boundary of this slab account for the horizontal heat transport by the oceans. Because the slab is thin it equilibrates much more quickly than a full ocean model. These equilibrated slab ocean simulations are a bit easier to think about than transient warming simulations with full ocean models in which there are changes in oceanic heat storage and transport. But in fact the analogous figure for a typical 21st century scenario is very similar, perhaps with a bit less compensation between the moist and dry components.
This extratropical dry flux is dominate by the eddy flux of sensible heat, proportional to [v’T’] where primes denote deviations form the zonal mean and the brackets an average over time, height, and longitude. The reduction in [v’T’] is potentially important for changes in weather — it must be associated either with a reduction in the typical temperature perturbations T’ or in the north-south winds v’ (or, conceivably, in the correlation between the two). This eddy flux is often thought of as having a diffusive flavor, with the eddies generating a downgradient turbulent diffusion of heat. One explanation that you sometimes see for the reduction in eddy sensible heat flux with warming is polar amplification, with a reduced north-south temperature gradient resulting in lower flux, given more or or less the same turbulent diffusivity. But the argument given here, if you can call it that (we haven’t really explained why the total poleward flux doesn’t increase as rapidly with warming as the extratropical latent flux), does not seem to have anything to do with polar amplification, at least explicitly. Is the explanation based on polar amplification misleading? I’ll just leave this question hanging for now.
Something else interesting happens due to this compensation between extratropical latent and dry fluxes. It is easier to see this effect if you increase the water vapor by an even larger amount than in these global warming scenarios. My colleagues and I have looked at this in a more idealized setting (Frierson et al 2007). This is an atmospheric model with water vapor, evaporation and precipitation and latent heat transport, coupled to a slab ocean. But there are no clouds and we assume a grey atmosphere with radiative fluxes a function of temperature only, so water vapor does not interact with the radiative transfer. The model climate is symmetric about longitude circles and about the equator. The model still has the complexity of deep moist convection in the tropics and storms modified by latent heat release in midlatitudes. We could call this model the mouse of climate models, in the spirit of the fruit fly model discussed in earlier posts. Rather than increase the temperature to see what happens when the water vapor increases, we just increase the water vapor more directly by increasing the saturation vapor pressure. I think this is a nice framework for addressing the kinds of questions exemplified by the discussion above, and I don’t think we understand this model very well.
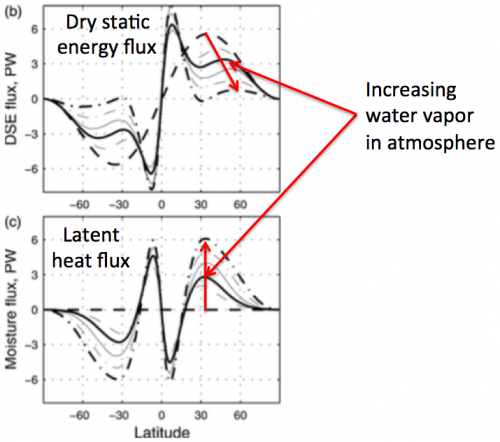 This figure from Frierson et al, shows the changes in the dry flux and the latent flux for very large changes in water vapor. We even go to the dry limit (the dashed line) with no water vapor in the atmosphere. It turns out, interestingly enough, that this model generates a more precise compensation between the changes in latent and dry fluxes than more comprehensive GCMs. But the point I want to focus on here is the poleward movement of the maximum in dry flux with increasing water vapor. The extratropical poleward latent flux peaks at a lower latitude that the dry flux. So when it increases, the compensating decrease in the dry flux is larger on the equatorward side of the dry flux maximum, causing a poleward shift in this maximum.
This figure from Frierson et al, shows the changes in the dry flux and the latent flux for very large changes in water vapor. We even go to the dry limit (the dashed line) with no water vapor in the atmosphere. It turns out, interestingly enough, that this model generates a more precise compensation between the changes in latent and dry fluxes than more comprehensive GCMs. But the point I want to focus on here is the poleward movement of the maximum in dry flux with increasing water vapor. The extratropical poleward latent flux peaks at a lower latitude that the dry flux. So when it increases, the compensating decrease in the dry flux is larger on the equatorward side of the dry flux maximum, causing a poleward shift in this maximum.
In many kinds of climate models we find that the atmospheric circulation and the associated climate regimes are shifted polewards with warming on average — in particular the latitude of the maximum kinetic energy in midlatitude storms shifts polewards. Can this shift be understood in more or less the same way as the shift in the dry flux? An increase in water vapor makes midlatitude storms more efficient at transporting energy since the latent heat flux adds constructively to the dry flux, but this increase in efficiency is greater on the equatorward side of the maximum in storm activity. So maybe we can think of the storms shifting towards the poles because that is where there is more work left to do, relatively speaking. There are an impressive number of competing ways of thinking about the poleward shift in circulation with warming. Maybe this one deserves a closer look.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



Hi Isaac,
Do you have a sense of how the poleward shift with warming compares in dry v. moist models? Perhaps the cleanest comparison would be in Dargan’s model, increasing the LW absorber both in the dry limit and in one or more moist cases. Motivation: I’m wondering how fundamental moisture is to this shift, but my physical intuition for these extratropical storms is quite lacking.
Thanks,
Spencer
I think the calculations you suggest are among the simulations described in Lu et al 2100. I have to reread this paper, and I am sure that there are other relevant papers as well. In that paper and elsewhere the argument is that the effects of an increase in the mean temperature on the poleward displacement of the westerlies ends up depending on the increase in dry gravitational stability and its effect on baroclinic instability. In the post, I was trying to push a somewhat simpler picture. .
Hi Spencer,
Cheikh Mbengue and I looked at the question of how far one can go in understanding poleward shifts of storm tracks etc. in a dry framework: Mbengue and Schneider (2013). It’s a little difficult to say exactly how much of the shift in more comprehensive, moist simulations is due to “dry” dynamics alone, because it is ambiguous to say what the relevant dry dynamics are. But storm tracks do shift poleward in a dry framework, by amounts somewhat smaller than but comparable to what is seen in moist simulations, for example, if mean temperatures and, with it, the tropopause height increase, or if only the static stability in the deep tropics increases. In the dry simulations in the above paper, the tropical static stability effect (which is ultimately a moist convective effect) dominates for changes representative of global warming. (A mechanistic model of how that works is in Cheikh’s thesis and will be in a paper soon.)
Tapio
I am an experimentalist but interested in studying the poleward moisture/heat transport problem with satellite cloud-tracking winds (so-called atmospheric motion vectors, or AMVs). My comment may be off the theoretical discussions but is related to the topic from an observational point of view.
In a comparison between AMVs and the reanalysis data, I found that the reanalysis winds often underestimate the poleward motion in the extratropical mid-troposphere, especially in the cloudy regions where these AMVs were acquired. This bias could be caused by a conservative treatment in the data assimilation approach, which tends to reject the high wind speeds that disagree with the modeled background winds in extratropical energetic systems.
This bias seems to be present in both ERA-I and MERRA reanalysis data, and makes me think what impacts it would create on poleward moisture and heat transport? If I understand your lecture note correctly, the majority of poleward fluxes (heat and moisture) come from cloudy regions where v’T’ or v’q’ are in the poleward direction. If v’ are systematically underestimated in these reanalysis datasets, I would expect the poleward fluxes be also. In other words, the system is pumping more heat to the Arctic than the estimated currently.
Because comparisons between models and reanalyses are so ubiquitous in current climate modeling, it is vital that we critically examine the latest reanalyses, especially for such basic quantities an the poleward heat and water fluxes. Thanks for your work on this.