Posted on April 13th, 2016 in Isaac Held's Blog
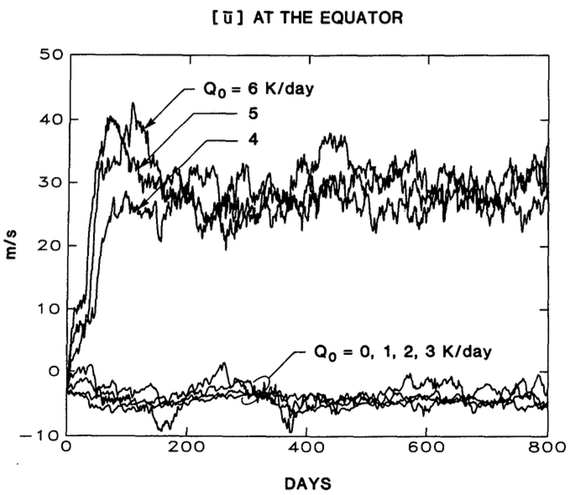
The average around the equator of the eastward wind in the upper tropospheric layer of the idealized atmospheric model of Suarez and Duffy 1992, for several different values of the strength of an imposed tropical heat source.
GCMs often play a conservative role as a counterpoint to speculation or idealized modeling regarding “tipping points” or abrupt climate change, in favor of gradual, more linear climate response to external forcing. Think of abrupt collapse of the AMOC (Atlantic Overturning Circulation) or the “death spiral” of Arctic sea ice. These high-end models may not always be correct of course, but I think they provide an appropriate null hypothesis that must be critically examined in the light of observational constraints, possible missing physics, etc. I’ll use the problem of equatorial superrotation to illustrate this point — also taking this opportunity to introduce this relatively obscure subject.
(Edited a bit for clarity, 4/16/16)
The figure is from a paper by Suarez and Duffy 1992 using an idealized two-level global model of the atmosphere. Two-level implies that the horizontal winds are defined at only two vertical levels, which we can think of as the lower and the upper troposphere. The interaction between an upper tropospheric and a lower tropospheric flow is the classic starting point for thinking about the fluid dynamics that produces midlatitude storms. The tropical Hadley circulation also seems, at least naively, to be representable to a first approximation with two levels. The first non-trivial climate models — models that simulate weather and that can be integrated over long enough periods to obtain the statistics of that weather — were two-level models, initially confined to mid-latitudes (Phillips 1956) and then moving to a global geometry (Smagorinsky 1963). It is tempting to continue to use two-level models to try to encapsulate our understanding of aspects of atmospheric climate, despite the fact that GCMs long ago moved to much finer vertical resolution. Suarez and Duffy use a dry version of such a model, starting with a control climate that is independent of longitude and then adding a longitude-dependent heat source in the tropics. As the magnitude of this heat source is increased, the model undergoes an abrupt transition to a very different climate. Is the atmosphere capable of making this kind of profound abrupt transition?
In the control climate of this model, the east-wind winds at the equator in the upper troposphere are (realistically) close to zero after averaging around the equator; in the new climate generated when the tropical heating is strong enough, the eastward winds at the equator increase dramatically. This alternative climate is referred as superrotating. Eastward midlatitude jets can be generated by simply taking a ring of air that is stationary with respect to the surface at the equator and moving it polewards, towards the axis of rotation, while conserving its angular momentum, but you can’t generate eastward winds at the equator that way. The interesting case is equatorial superrotation — equatorial winds in the direction of and faster than the rotation of the surface at the equator. Equatorial superrotation (which I’ll abbreviate as just “superrotation”), is seen in many planetary atmospheres. Is the abruptness of this transition to a superrotating state realistic?
And does this issue have any conceivable connection to global warming? The simplest way to make a case for potential relevance is to point to simulations of the very warm Eocene (especially that of Caballero and Huber 2010). These do produce strong equatorial superrotation, and they show some acceleration towards larger superrotation with increasing warming, albeit at much warmer temperatures than are relevant for the next century — but the transition is not nearly as abrupt as in the figure above. Most importantly, there is only a barely significant hint of an increase in westerlies near the tropical tropopause in GCM projections for the next century (Figure 12.19. in Ch. 12 of the AR5/WG1 report.).
I discuss this issue in this lecture from 1999, where I talk about some of the underlying mechanisms that favor superrotation and that might create an abrupt transition. One important ingredient is the excitation of Rossby waves (see post #57) that propagate out of the tropics into midlatitudes. If the tropical Rossby wave source increases — this is what increasing the heat source in Suarez and Duffy does — there should be a tendency towards superrotation. If the tropical wave source increases with warming, then warming should produce some superrortation (holding everything else fixed). Abruptness then seems to depend in large part on the fate of Rossby waves excited in midlatitudes that propagate into the tropics. But these arguments are sufficiently qualitative that they could be applied to full GCMs as well as the two-level model.
The Suarez-Duffy paper did not attract much attention. I feel a bit guilty for not having done more on this problem in recent years. I am not even sure how robust the two-level result is to the details of the model formulation. But I suspect that we might learn something significant about the atmosphere by understanding better the susceptibility to this abrupt transition in idealized atmospheric models, including this dry two-level model. And this understanding might in turn be relevant to how we judge the credibility of this aspect of our high-end simulations.
I would put a very low number on the probability of a big surprise in the response of equatorial winds to warming in the coming century. But it would not be infinitesimal. This superrotation problem still troubles me because there are aspects of GCMs that are uncertain that might be relevant to this issue. For example, the vertical redistribution of horizontal momentum by small-scale moist convection in the tropics could affect the tendency towards superrotation — and this momentum exchange could be sensitive to the spatial organization of convection (into squall lines etc) that is not well resolved in current models. In addition, Cabellero and Huber and others point to Madden-Julian Oscillation (MJO)-like phenomena as playing a role in the transition to superrotation, yet the MJO, an intensely studied mode of variability in the tropics on a 30-50 day time scale, is not simulated very robustly in current GCMs. But I would need much stronger arguments than anything I currently have to override (the thankfully rather boring) GCM simulations and push this issue as important for anthropogenic climate change.
In this case and in some others like it on potential tipping points, such as AMOC collapse, GCMs do seem to provide a conservative null hypothesis. Even though I may have an argument or idealized model suggesting that some abrupt climate response might be possible, if our GCMs — by which I mean the best simulators of the climate that the world can come up with — do not show this behavior then I cannot just decide to prefer my theory to the GCM simulations. I need a compelling argument that the GCMs do not include some key ingredient or are inconsistent with observations in a way that is relevant to the response in question.
I hope to return to the topic of superrotation in upcoming posts — there are several new interesting papers on this topic.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



With regard to simple models, GCMs, and abrupt responses: the recent paper by Boos and Storelvmoa (doi:10.1073/pnas.1517143113) seems like a nice example. They show that GCMs do not give an abrupt response of the monsoon to radiative forcing unlike a simple model, and they are then able to show what is missing from the simple model that causes the discrepancy.
Another example: Wagner and Eisenman 2015 (https://doi.org/10.1175/JCLI-D-14-00654.1) on sea ice. They show that the abrupt responses in the simplest energy balance models or single column models of sea ice go away with very modest additional complexity (namely, combining the two classes of models). And this is more in line with GCM simulations.
Hi Isaac, as a newcomer to the comments thread let me first say thanks for this blog, which is a real source of inspiration for many of us. Regarding the Suarez & Duffy and Saravanan models, I think a potentially crucial way in which they differ from reality is in the lack of a seasonal cycle. The cross-equatorial Hadley cells that result from the seasonal cycle give an annual-mean deceleration at the equator which largely balances the momentum convergence by tropical eddies, with midlatitude eddies playing a smaller role (that’s the balance in our GCM work, anyway). The important thing is that the Hadley cell drag isn’t particularly sensitive to the structure of the mean flow, and therefore isn’t subject to the same kind of eddy-mean flow feedback that most likely explains the abrupt transition in the Suarez & Duffy paper. In any case, there’s certainly enough complexity even in the simple models to leave ample room for surprises, so it would be interesting to revisit the Suarez & Duffy study but adding a seasonal cycle to test the robustness of the bifurcation.
Rodrigo, thanks.
Regarding the seasonal cycle, it is plausible that it acts to prevent superrotation. I am not sure that this is the key to the distinction between the 2-level and full GCMs, but all I have to go on is the model that I built in the 1990′s (mentioned in the lecture linked to above but never published) — a 2-level model with a seasonal cycle and realistic boundary conditions — that still superrotated.
I am interested in the claim that the basic momentum balance of relevance is between the Hadley cell bringing up low angular momentum air from the surface and acceleration by equatorially-generated waves, with the drag due to midlatitude eddies playing a secondary role. I was under the impression that weakening the latter made it easier to superrotate — ie Laraia and Schneider, DOI: https://doi.org/10.1175/JAS-D-15-0030.1. If the drag due to midlatitude eddies does not penetrate all the way to the equator it will not show up in the equatorial momentum budget, but its effect will still be felt through the strength of the upwelling in the Hadley cell presumably.
This also brings to mind a paper (DOI: https://doi.org/10.1175/JAS-3312.1 that Karen Shell and I wrote in 2004, using a very simple axisymmetric shallow water model to show that once you begin superrotating due to some applied torque at the equator, and the Hadley cell weakens in response, the loss of this Hadley drag can itself lead to an abrupt transition to even stronger superrotation, even if the applied torque is fixed.
Yes, superrotation can certainly happen even in the presence of a seasonal cycle (as in the GCMs), I’m just curious as to how it might affect the nature of the transition to superrotation. And I agree, the effect of drag by upward flow in the Hadley cell is an interesting way in which eddy-mean flow interaction could come back into the picture.