Posted on May 23rd, 2016 in Isaac Held's Blog
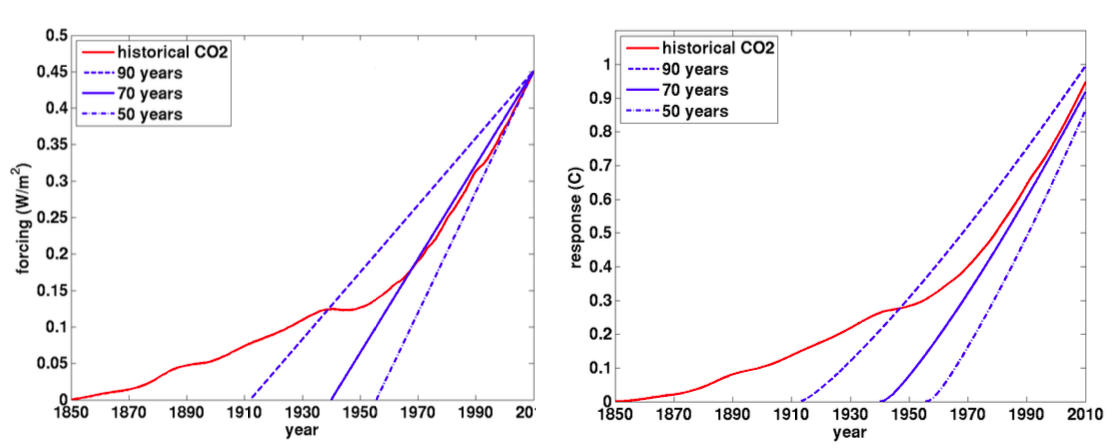
The radative forcing (left) and global mean temperature response (right) using a simple GCM emulator, for the historical CO2 forcing (red) and for the linearly increasing forcing consistent with the simulations used to define the transient climate response (blue), for 3 different ramp-up time scales, the 70 year time scale (solid blue) corresponding to the standard definition.
The terminology surrounding climate sensitivity can be confusing. People talk about equilibrium sensitivity, Charney sensitivity, Earth system sensitivity, effective sensitivity, transient climate response (TCR), etc, making it a challenge to communicate with the public, and sometimes even with ourselves, on this important issue. I am going to focus on the TCR here (yet again). The TCR of a model is determined by what appears to be a rather arbitrary calculation Starting with the climate in equilibrium, increase CO2 at 1% per year until doubling (about 70 years). The global mean warming of the near surface air temperature at the time of doubling is the TCR. In a realistic model with internal variability, you need to do this multiple times and then average to knock down the noise so as to isolate the forced response if you are trying to be precise. If limited to one or two realizations, you average over years 60-80 or use some kind of low-pass filter to help isolate the forced response. Sometimes the TCR is explicitly defined as the warming averaged over years 60-80. Although I have written several posts emphasizing the importance of the TCR in this series, I would like to argue for a de-emphasis of the TCR in favor of another quantity (admittedly very closely related – hence the modesty of this proposal.)
If you talk to someone about the TCR you have to explain why this idealized 1%/yr scenario is of interest. From my perspective, the importance of the TCR stems from its close relationship to the warming from the mid-19th century to the present that can be attributed to the CO2 increase. There is a growing literature on estimating TCR from observations, using the instrumental temperature record over this time frame. But these studies are not direct estimates of TCR; they are estimates of the warming attributable to the CO2 increase which are then converted to TCR by assuming that the warming is proportional to the CO2 radiative forcing. If forcing due to a doubling of CO2 is and the forcing due to the observed increase in CO2 over the period T = (T1 T2) is
(T) then
TCR = WACO2(T)/
Here I have defined WACO2(T) as the global mean Warming Attributable to CO2 over the time interval T and I have set . For the rest of this post, I’ll just assume that T = (1850, 2010). For this period,
is about 0.45.
The past warming attributable to CO2 is itself important as a constraint on models used to project this warming into the future. Whether your model is a simple extrapolation or an energy balance model or a full GCM that simulates climate by simulating weather, you obviously want the model you are using to be consistent with the past warming.
Estimating WACO2(T) from observations over the past century or so is far from straightforward, due primarily to the uncertainty in the cooling due to anthropogenic aerosols, but also due to the presence of other forcing agents, including other well mixed greenhouse gases, as well as internal variability, But what’s the point of converting someone’s estimate of the range of values of WACO2 consistent with observations into the corresponding range of TCR values? The point is simply that the latter has become a standard for the comparison of GCM responses, so the range of TCR estimates from models is readily available. But this does not seem like a very good reason to try to communicate the importance of the TCR value rather than the more obviously relevant WACO2(T).
How good is the proportionality assumption TCR = WACO2(T)? And if it is good, why? For concreteness I’ll use a very simple three time-scale fit to the response of a particular GCM to an instantaneous doubling of CO2. The model is GFDL’s CM3 and the fit is described in Winton et al 2013. The response takes the form
with = [1.5, 1.3, 1.8]K and
= [3, 60, 1000] years. I have rounded off the time scales a bit. Since this model is linear you can scale this response to that for an infinitesimal increase and then add up the responses to the forcing over time for any CO2(t). (See the discussion of the response to volcanic forcing in post #50,)
I carried it along for these calculations,, but the very long millennial time scale present in the GCM has negligible effect on WACO2 or TCR , so this is really a two-time scale model for our purposes. And you may have noticed that this is a a rather sensitive model. But keep in mind that it is linear, so if you multiply all of the ‘s by the same factor you change the amplitude of all responses, including WACO2 and TCR, by this same factor.
[In the calculations to follow, I’m assuming that the radiative forcing due to CO2 is exactly logarithmic in CO2 concentration, so 1% increase/yr is a linear increase in radiative forcing.]
The red line in the figure on the left above shows the CO2 radiative forcing from 1850 to 2010 from GISS. The solid blue line shows the linear increase in forcing over 70 years that ends up at the same value of forcing at 2010 as the red line. This is the forcing due to a 1%/year increase multiplied by — or, equivalently, it is the forcing due to a
%/yr increase for 70 years. Also shown with the blue dashed lines are the linear forcing trajectories that reach the same point in 2010 but increasing the 70 year interval to 90 years or decreasing it to 50. The 70 year linear increase at
%/yr is evidently a pretty good fit after 1960. It’s not relevant whether a 1%/yr increase is larger than the increase in CO2 forcing since we are assuming linearity and normalizing the TCR anyway. The key is that a linear fit to the recent period of rapid increase in CO2 forcing requires roughly 70 years starting from zero.
The figure on the right shows the responses of the three-time scale model to these forcing trajectories. The standard (70yr) TCR after normalization underestimates the WACO2 (the red curve) by about 3%, which is basically negligible given the the uncertainties in TCR that we are concerned about. My eyeball estimate of the error, given the forcing that is missed by this linear approximation before 1950, keeping in mind the 60 year intermediate e-folding time in this model, would have been a bit more than this, so I have checked this result a couple of times — which does not guarantee that I did not make a mistake, of course, (It seems that the error made by missing the response to the increases in CO2 in the first half of the 20th century is canceled in part by the fact that the linear fit in the more recent period is not perfect.) Even if you make the sub-optimal choices of 50 or 90 years for the ramp-up, the errors are only of the order of 10%.
So the approximation WACO2 = TCR looks good, at least for this particular response function. If you want to modify the model to create a larger difference, you will have to decrease the relative importance of the fast response that occurs on time scales shorter than the time scales of the CO2 evolution itself and put more weight on the longer time scales. Using discrete response times is not the only way of emulating a GCM’s response function. Diffusive models have a long history in this regard. But as long as the fast response is as large a part of the response to centennial-scale forcing as it is in GCMs (see Geoffroy et al 2013) you won’t get very much of a discrepancy.
We could de-emphasize the 1% year simulation in favor of just simulating the response to the historical CO2 increase. This simulation is performed routinely by some groups, but for the CMIP projects, including the upcoming CMIP6, it is the response to the historical evolution of all of the well-mixed greenhouse gases (WMGGs) that is typically requested, without breaking out the CO2 contribution. This raises another issue — the validity of assuming that you can get the response to CO2 from the response to the full set of WMGGs by simply normalizing by the ratio of the radiative forcings. Given questions about how best to define radiative forcing (a good topic for another post), this adds an unnecessary layer if you is are primarily interested in a model’s response to CO2.
Rather than focusing on TCR itself, especially when discussing this topic outside of scientific circles, we should think of it as just a standard way of estimating WACO2 for a model, a technique that could be improved if desired. Perhaps what we need is a good acronym for the warming attributable to CO2. WACO2 seems less that ideal.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



This is perfectly laid out. The lesser alternative is probably to have something called an effective TCR, where the modifier implies that CO2 effectively pulls in the other GHG’s along with the baseline impact of just CO2.
It’s frustrating to read blogs such as And Then There’s Physics, where every post is the same confusing message of presenting the dry definition for TCR without the necessary context. One clear post is all that is required. Thanks.