70. Spherical rotating radiative-convective equilibrium

Posted on June 3rd, 2016 in Isaac Held's Blog

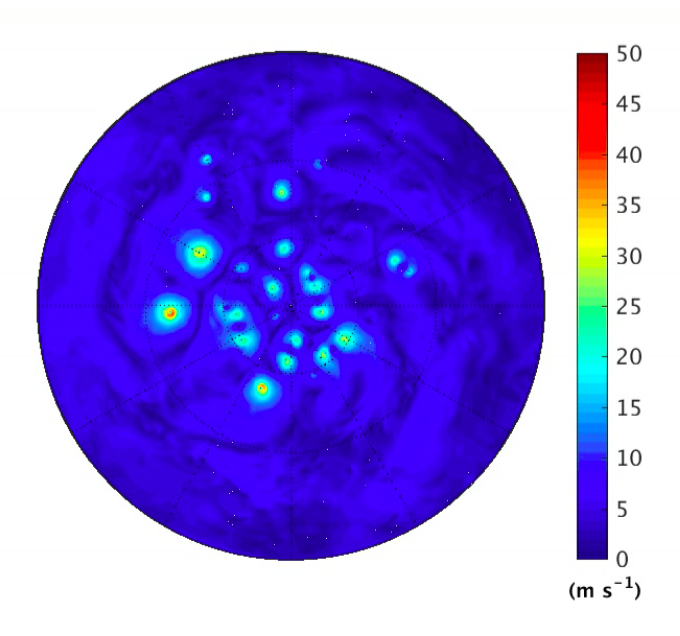
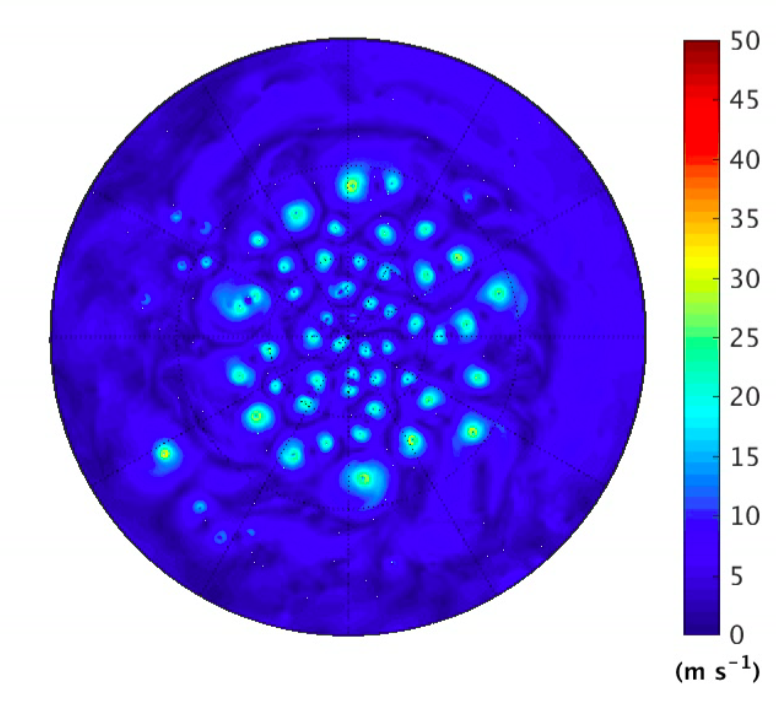Snapshots of near surface wind speed in simulations of spherical rotating radiative convective equilibrium, as described in Merlis et al 2016.  A full hemisphere is shown, the outer boundary being the equator.  The surface temperature is prescribed at 307K in the upper panel and 297K in the lower panel.  For animations of one month simulations click on (307, 297).

Continuing a recurrent theme in these posts, I’ll describe yet another idealized framework for thinking about the climatology of tropical cyclone (TC) formation.  In this setup, we assume a rotating sphere with a homogeneous surface  — water-saturated; no continents; surface temperatures prescribed to be uniform over the entire sphere.  There are no seasonal or diurnal cycles in the insolation (and we prescribe a spatially uniform ozone distribution as well).  So the only source of spatial inhomogeneity is the rotating sphere.  For our thin rapidly rotating atmospheric spherical shell, the key inhomogeneity is the latitude dependence of the strength of the horizontal component of the Coriolis force, the “Coriolis parameter”, where is the latitude. The amplitude of increases from the equator, where it vanishes, to the poles.  This latitudinal gradient in is critical for TC evolution.  In the Northern Hemisphere, the increase of with latitude causes cyclonic vortices to drift north and west with respect to the larger scale flow in which they’re embedded, a process known as -drift.  ( is the conventional symbol used to represent the northward gradient of .)

Being spatially inhomogeneous this model is potentially a lot more complicated than the homogeneous model described in Post #43 that uses a a doubly-periodic  “-plane” geometry, ie with a constant strength of the Coriolis force .  The intriguing result in the latter setup, but also the problem with that setup, is that the domain fills up with tropical cyclones.  These TCs are so long-lived and interact so weakly that there is rarely room for another storm to form.  The -plane framework is fascinating to me but it seems more suited to studying mature storm structure rather than new storm formation (genesis).  On the sphere -drift carries these storms polewards, clearing out the tropical regions where the storms develop and making plenty of room for new storms.

Compared to the more standard aquaplanet simulations described in posts #42 and #67, this setup has the simplification of surface temperatures that are uniform in latitude as well as longitude.  When you prescribe more realistic surface temperatures with an equator-to-pole gradient, you get large east-west winds and instabilities resulting in midlatitude storms.    These aquaplanet frameworks may be ideal for studying the interactions between TCs and extratropical storms, but it is also nice to get rid of these storms altogether to see how the TC’s behave on their own, which is just what the uniform sea surface temperatures do.

There was some earlier work with more or less this same setup, but focusing on the mean precipitation rather than TC statistics — such as Kirtman and Schneider 2000, who describe a model in which the tropical precipitation still gathers itself into a sharp intertropical convergence zone at the equator despite the absence of any spatial inhomogeneity in the lower boundary condition or the incident solar flux.  The theory for this kind of organization of the mean precipitation is itself of interest, but this earlier work did not discuss TC simulation.  Tim Merlis, Wenyu Zhou, Ming Zhao and I were discussing this framework — it has the nice feature that anyone with a GCM can configure it easily — but I was personally rather discouraged by the complexity coming from the inhomgeneity of both the mean climate and the TCs.   However, more recently Shi and Bretherton 2014 returned to this setup but focusing on TCs, with a lot of interesting results that caught our interest.  So we tried our hand at this framework in Merlis et al 2016. We used somewhat higher horizontal resolution (about 50 km) and focused in particular on the response to increasing surface temperatures.

Most importantly from my perspective is that this model and the homogeneous -plane model of Zhou et al 2014 and post #43; the aquaplanet model with SSTs a function of latitude of Ballinger et al 2015 and Post #67, the “slab-ocean” aqua-planet of Merlis et al 2013 and Post #42, and the atmospheric model with realistic boundary conditions of Zhao et al 2009 and Post #2 all use exactly the same atmospheric model.  They differ only in their boundary conditions, at the surface and incident solar flux at the top of the model, and in the domain geometry.  The model with realistic boundary conditions does a pretty good job on the global number of TCs, their seasonal cycle, the response of TCs to ENSO, etc.  Having this realistic point of contact is important to help justify the idealized configurations — ie, if they help us understand the realistically configured model they may help us understand nature. I am struck by the variety in these simulations, which I think gives us a lot to think about when trying to understand the TC climate more fundamentally.

The figure at the top shows a snapshot (and animations) of the near-surface wind speed for simulations with two different surface temperatures, 297 and 307.  The basic picture is of TC genesis in low latitudes , after which the storms migrate poleward and congregate into a swarm of cyclonic vortices around the pole.   The situation in the polar cap resembles the -plane simulation of Post #43.  This evolution has gone on for some time before the month shown in the animation, so we think the distribution of vortices has equilibrated.  New storms entering the polar cap crowd are compensated by some merger or destruction of vortices already congregated there, so this cap of vortices does not seem to be growing, which is nice since that leaves the generation region more realistically free of crowding by pre-existing vortices.

In the colder case, there are obviously a lot more vortices with less space between them, and the crowd of vortices surrounding the pole has grown — to the extent that any more growth could interfere with the generation process in low latitudes.  It is not only the number of vortices but the generation rate is also much higher in the case with colder temperature, by roughly a factor of 4.  Admittedly, this is a big change in temperature but even when you look at the reduction in genesis frequency per degree warming  it is quite a bit larger than the reduction that you see in this model when configured with realistic boundary conditions.  (You may recall that the aqua-planet slab ocean model described in Post #42 actually has the frequency of TC formation increasing with increasing surface temperature.)

I think this may be a good setup for looking at how different global model formulations affect TC genesis frequency — and the temperature dependence of this frequency — as long as the -drift is successful at cleaning out the development region.   The expansion of the polar cloud of cyclones with decreasing temperature is itself interesting but a problematic distraction if you want to focus on genesis in a realistic setting of relatively little interference from pre-existing TCs.  One could add damping (increased surface friction) to the polar regions to try to destroy these storms and prevent their accumulation and avoid this interference.

[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]