Posted on March 19th, 2011 in Isaac Held's Blog
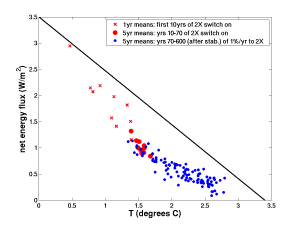 The co-evolution of the global mean surface air temperature (T) and the net energy flux at the top of the atmosphere, in simulations of the response to a doubling of CO2 with GFDL’s CM2.1 model.
The co-evolution of the global mean surface air temperature (T) and the net energy flux at the top of the atmosphere, in simulations of the response to a doubling of CO2 with GFDL’s CM2.1 model.
Slightly modified from Winton et al (2010).
Global climate models typically predict transient climate responses that are difficult to reconcile with the simplest energy balance models designed to mimic the GCMs’ climate sensitivity and rate of heat uptake. This figure helps define the problem.
Take your favorite climate model, instantaneously double the concentration of in the atmosphere, and watch the model return to equilibrium. I am thinking here of coupled atmosphere-ocean models of the physical climate system in which
is an input, not models in which emissions are prescribed and the evolution of atmospheric
is itself part of the model output.
Now plot the globally-averaged energy imbalance at the top of the atmosphere versus the globally-averaged surface temperature
. In the most common simple energy balance models we would have
where both
, the radiative forcing, and
, the strength of the radiative restoring, are constants. The result would be a straight line in the
plane, connecting
with
as indicated in the figure above. The particular two-box model discussed in post #4 would also evolve along this linear trajectory; the different way in which the heat uptake is modeled in that case just modifies how fast the model moves along the line.
The figure at the top shows the behavior of GFDL’s CM2.1 model. The departure from linearity, with the model falling below the expected line, is common if not quite universal among GCMs, and has been discussed by Williams et al (2008) and Winton et al (2010) recently — these papers cite some earlier discussions of this issue as well. Our CM2.1 model has about as large a departure from linearity as any GCM that we are aware of, which is one reason why we got interested in this issue.
As indicated in the somewhat cryptic legend, we use two different types of simulations to make this plot. One is the instantaneous doubling of referred to above. We show annual means for the first 10 years (with each cross in the figure an average over 4 realizations to knock down the noise, branching off at different times from a control simulation) and then show 5-year means up till year 70, again averaging over 4 realizations. Because these integrations do not go out far enough to probe the slower long term evolution, we then append a single realization of the standard calculation in which
is increased at 1%/year until the time of doubling (year 70) after which it is held fixed. We plot 5-year averages from this calculation, starting in year 70, so all points in the figure correspond to the same value of
. 600 years still isn’t enough to equilibrate, but as long as something fundamentally new doesn’t happen in the model on longer time scales one can extrapolate to
to get an estimate of the equilibrium temperature response. The two simulations match up nicely in year 70, as one expects if the 1%/yr case resides during its ramp-up phase in the intermediate regime (post #3). Because of the curvature of this trajectory, the temperature change at year 70, about 1.5-1.6K (the transient climate response (TCR)) is smaller than we might expect from the model’s equilibrium sensitivity and the model’s value of
at that same time.
One’s first reaction might be to say — well, there is nonlinearity in the model in the sense that is effectively a function of
. But I think there is agreement that the underlying dynamics is still best described as linear; it’s just that the global mean energy balance is not a function of the global mean surface temperature. A more general linear model assumes that the global mean energy balance is a linear functional of the surface temperature field, with different spatial structures in surface temperature perturbations, even if they have the same global mean, generating different perturbation to the global mean energy balance.
Think of some atmospheric model equilibrated over a prescribed surface temperature distribution. This temperature distribution is the input to the model. The model outputs climate statistics of interest, including the global mean energy balance. If the relation between input (surface temperatures) and output (global mean energy balance) is linear, we can write
Brackets denote a spatial average over the surface and is the position on the surface. The scalar radiative restoring constant
has been replaced by
. (By the way, I am not assuming here that the top-of-atmosphere energy balance in some small region is only a function of the surface temperature in that same region — the relation between these two is non-local due to mixing in the atmosphere.)
The simplest case is when temperature evolves in a self-similar manner, i.e., growing with a fixed spatial structure:
(I have normalized things so that ). The effective radiative forcing for temperature perturbations with this structure is
.
If temperatures perturbations have a different structure, , then we need to replace
with
. But suppose that the temperature perturbations are the sum of two patterns with relative contributions varying in time:
,
with . This gives us enough freedom to get evolution off the classic linear trajectory. But we haven’t learned anything yet about how and why the ratio of
to
is evolving in time.
One way of analyzing any linear system is through the frequency-dependence of the response to perturbations. Low frequency and high frequency forcing can result in different radiative restoring strengths if they result in different spatial structures in the response. Evidently, the low frequency component controlling the late time evolution in the response to doubling of CO2 is characterized by a structure that is restored less strongly than is the fast, early response. Why would that be?
The story seems to be something like this: The atmosphere tends to be most unstable to vertical mixing in the tropics, where the surface temperature are warmest, but the oceans are most unstable to vertical mixing at high latitudes, where the surface temperatures are the coldest. It is in the subpolar oceans that the mixing between surface and deeper waters is the strongest. One expects these regions to be a major source of the difference between fast and slow responses, with the slow responses having larger subpolar ocean warming. This effect tends to mix out to other high latitude regions, so the high latitude amplification of the response is typically larger in the slow response.
We now have to argue why a pattern with larger high latitude amplification is restored less strongly. This is more complicated. A part of the explanation seems to be that the surface is less strongly coupled to the atmosphere in high than in low latitudes, so the surface warming has a harder time affecting the radiation escaping to space. But a big part also seems to be played by different cloud feedbacks that come into play in the fast vs the slow responses, the clouds reacting to the different atmospheric conditions that occur when the subploar ocean warming is held back or is given time to respond.
One can still try to save the global mean perspective. Winton et al (2010) pursue this line of reasoning by referring to the “efficacy of ocean heat uptake”. The idea here is that the difference in spatial structure of the fast and slow responses can be attributed to the heat being transferred from shallow to deeper ocean layers. Putting aside the question of how this heat transfer is controlled, one can try to think of it as a different kind of “forcing” of the near-surface layer, alongside the radiative forcing. The response to heat uptake, being focused in high latitudes, naturally has a spatial structure that is more polar amplified than the response to CO2 (with the heat uptake fixed), so it experiences a smaller restoring strength. The effects of the surface cooling due to heat uptake by deeper layers is amplified, slowing down the initial fast warming more than one might otherwise expect. This picture has the nice feature that it ties the timing of the change in spatial structure directly to the saturation of the heat uptake. You may want to think about how to capture this effect with a simple modification of the two-box model described in earlier posts.
One moral of this story is that forcing a global mean perspective on the system can make things look more complicated than they actually are, making the response look superficially nonlinear when it is still quite linear.
Another moral is that the connection between transient and equilibrium responses may not be as straightforward as we might like, even when only considering the consequences of the physical equilibration of the deep ocean, leaving aside things like the slow evolution of ice sheets.
[The views expressed on this blog are in no sense official positions of the Geophysical Fluid Dynamics Laboratory, the National Oceanic and Atmospheric Administration, or the Department of Commerce.]



I’m not sure I understand this correctly. The atmospheric “resistance” to radiative loss of heat to space seems to be substantially lower in cold regions than in warmer regions (not surprising in light of the low atmospheric water vapor in cold climates). The difference in temperature between the surface and the top of the troposphere, divided by the watts per square meter radiated, seems significantly higher in the tropics than in polar regions.
So I am puzzled that your post appears to suggest radiative loss to space is more inhibited at high latitudes a long time after a step change in forcing. Is this just related to a slow change in the moisture content of the atmosphere at high latitudes due to very slow ocean surface warming at high latitudes?
Steve, I guess I am returning the favor in not being sure that I understand your comment. I an not clear what you mean by “atmospheric resistance to radiative loss of heat to space seems to be substantially lower in cold regions”. It is the resistance (associated with the loss to space) experienced by an attempt to change the surface temperature in the model that is lower in high latitudes — ie, the atmosphere is providing more of a buffer between the surface and the radiative loss. This is the opposite of what you might expect from water vapor. Part of the answer to what the model is doing is that surface heating just doesn’t spread as far into the troposphere in high latitudes — you can think of it in large part as remaining below the average level at which infrared photons escape to space. (This is often referred to as lapse-rate feedback.) But in the specific model being discussed here, the main factor explaining the difference in sensitivity between fast and slow responses — or between the response to CO2 forcing with and without the effect of ocean heat uptake — is clouds (this would primarily be shortwave) — see table 1 in Winton et al (2010) referenced above.
I had played with the CM2.1 runs available on the GFDL portal in response to your post #27. Data were only available for 200 (doubling) or possibly 300 years (one of the RCP runs). Large amplification of polar warming was only visible at the North Pole. However looking at the plots in your post 11 (thanks for the response) I can see that somewhere after that, the amplification at the South Pole begins to catch up. I had not found a picture of this previously though I would guess it to be in several papers I haven’t read. Intuitively it makes sense in terms of the ice mass being much less strongly coupled to ocean circulation (being mostly on land). I hope this makes sense to you because it helps my mental model.
The asymmetry of polar amplification has been discussed extensively over the years, some early papers are by Bryan et al (1988)) and Stouffer et al (1989). The key is the efficient and deep uptake of heat in the Southern ocean in these models, creating a very large effective heat capacity locally. It is certainly odd that the lack of trend in Antarctic sea ice is used by some as a critique of global warming models when this is exactly what most models predict. The rapidity of warming in the Southern Ocean and around Antarctica is, however, one of the things that could be sensitive to the explicit simulation of mesoscale eddies in ocean models (post #29).
I’ve given those papers a quick read, thank you for the links. In an attempt to tie back in to what you wrote to Steve Fitzpatrick regarding cloud feedback, I find it hard at this moment to relate the two results that 1) net polar amplification increases over time, first over decades to several centuries as the Arctic Ocean adjusts, then over an even longer time period as the heat uptake in the Southern Ocean relaxes; all of which tends to increase δT/δN due to the greater atmospheric buffer at the poles, while 2) there is also an increase in positive cloud feedback over time somehow related to relaxation of ocean heat uptake generally as in Winton et al 2010. Is the temporal coevolution of these phenomena synergistic, or a coincidence? – or perhaps a parallel question, is it a coevolution in latitude and time or merely time?
PS – While writing the questions above it occurred to me that the cloud effect could have something to do with the energy balance of the oceanic mixed layer or top few meters of the ocean even.
Isaac and Bill,
Thanks for the interesting discussion here. I agree with Isaac in his response.
What I want to add is that even in the slab-ocean simulations, i.e., without the change in oceanic heat uptake, the asymmetry of polar amplification still exists ( Figure 1 of the link ). So the (spatial) asymmetry may also be related to the lack of ice-albedo feedback over the Antarctic continent and the lack of polar atmospheric sensible and latent heat transport over the Antarctic region ( possibly related to the much weaker stationary wave activity in the southern hemisphere). Accordingly the cloud feedback are also different.
About the temporal asymmetry of polar amplification, not only the ocean area are larger in the southern hemisphere, the vertical mixing of heat over the Southern Ocean can also be very deep due to the eddies associated with the strongest ocean current – ACC. Both may contribute to the larger heat inertia in the southern hemisphere. Therefore, as Isaac have said, ” The rapidity of warming … could be sensitive to the explicit simulation of mesoscale eddies in ocean models”.
Isaac,
I’m not a professional at this, so I hope you’ll forgive the amateur question.
My query is to do with the time-dependence of the rate of response to a time-dependent forcing. In your examples, you consider either a step or ramp change in forcing extended over a long period. But in practice, the forcing varies diurnally and annually (and even inter-annually) with a far greater amplitude, and the step is in the mean. While I can see that averaging this over a year is valid (in a linear system) when calculating the equilibrium, I’m not so sure about the lagged response due to the thermal inertia. It seems to me that the penetration depth, and hence the surface heat capacity, are frequency dependent.
By smoothing out the annual variation in the models, I assumed it was implicit that the top-most surface layer that varied in temperature both up and down with the forcing was being neglected, as it equilibrates on timescales shorter than were being considered, that the ‘surface box’ was the layer below this that was still part of the mixed layer and hence responded within a few years, and the second box was the deep ocean. In essence, the heat capacity is a continuous function of frequency related to rate of change of penetration depth, ranging from the ‘surface’ heat capacity to the ‘deep ocean’ heat capacity that we’re extracting two slices from, based on our chosen annual time scale. Beta relates to the rate at which heat can escape upwards from this layer.
If the slope of F – beta T versus T is not constant, my immediate naive interpretation would be to suspect that beta was not constant over all time scales. Should we expect it to be?
Just as you can get dependence on frequency with the differing horizontal spatial structure of the changes, wouldn’t the same apply to the vertical spatial structure? Can you clarify for me why (or if) the changing penetration depth over time is expected to have negligible effect on the local dynamics?
As an aside, I found it useful in thinking about your 2-box model to plot the T versus To direction field. You can then see that the two eigenvectors of the system of differential equations correspond to the trajectory of the fast and slow responses. The system moves fast parallel to one eigenvector until it lies on the line through the equilibrium parallel to the other, and then moves slowly along this line towards the equilibrium. I’d be interested to know if anyone has plotted a similar direction field for an actual GCM. Does it have the same structure?
The reason that the horizontal structure of the response changes as the model equilibrates is precisely that the lower frequencies penetrate more deeply, as you say. In the two box model, one has to somehow make the outgoing flux a function of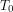 to mimic this effect.
to mimic this effect.
Rephrasing your proposal a bit, plotting GCM evolution in the (global mean surface temperature, total ocean heat content) plane in response to different forcing scenarios would be interesting, but I doubt that a two-box model would be able to mimic this evolution quantitatively.
I would definitely like to see more systematic analyses of the response of GCMs as a function of the frequency of periodic CO2 or total solar irradiance forcing.
Apologies for commenting after such a long delay, but I happened to spot your above statement doubting that a two-box model would be able quantitatively to mimic GCM evolution in the (global mean surface temperature, total ocean heat content) plane in response to different forcing scenarios.
As it happens I have just been looking into this point in connection with the new J Climate paper by Tim Andrews, Jonathan Gregory and Mark Webb dealing with the evolution of surface temperature in GCMs. They use Gregory plots for global evolution, but GMST vs total OHC plots can obviously be derived from those. They find distinct changes of slope after ~20 years for the CMIP5 model mean and two Met Office models; I imagine many other models behave similarly. This behaviour appears consistent with your findings for GFDL models.
I have worked out how to emulate the sort of two-timescale feedback behaviour typical CMIP5 models show using a modified 2-box model. Although with suitable parameter choices a standard 2-box model can, I think, emulate the global temperature response with time-varying feedback despite using a constant feedback, it can’t also get the radiative imbalance behaviour correct – the Gregory plot line is still straight. By using different feedback parameters for the two boxes I am able to emulate bent Gregory plot lines. I find that when doing so for HadGEM2-ES, using the same parameter settings I can get a pretty good fit to the Gregory plots both for Tim Andrews’ abrupt 4x CO2 and his 4x CO2 1% p.a. up-down ramp HadGEM2-ES simulations.
One way or the other, to capture this behavior you need to emulate the changing spatial structure of the warming (with high latitude warming delayed) and the consequences of this changing structure on the relationship between net TOA flux and GMST (high latitudes restored more weakly than low latitudes) — which sounds like what you are doing by giving the two boxes different feedback strengths.
Thanks for responding.
Although I’m capturing the time variation of feedback strength by giving different feedback strengths to the two boxes, I don’t think it logically has to be the case that this corresponds to what is going on in high latitudes – that may depend on the GCM(s) being emulated.
In fact, according to the new Andrews et al paper, for CMIP5 AOGCMs as a whole about 60% of the change in feedback parameter comes from the tropics (30N-30S), particularly the Pacific, with only a minority from mid and high latitudes. However, the CMIP5 mean tropical Pacific warming pattern in years 1-20 of the abrupt 4x CO2 experiment shown in the Andrews paper seems dissimilar to the actual warming pattern over the last ~30 years, when GHG forcing almost certainly dominated.
i discuss the 30 year trend pattern a bit in post #45
I think I understand this but perhaps in slightly different terms:
The important point that you are trying to get across is that the model results can be explained without recourse to non-linearity in .
.
That is is a function of position only
is a function of position only  not of
not of  or
or 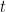 .
.
Assuming that the forcing due to WMGGs to be separable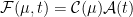 where
where ![[\mathcal{C}] \equiv 1](https://s0.wp.com/latex.php?latex=%5B%5Cmathcal%7BC%7D%5D+%5Cequiv+1&bg=ffffff&fg=000&s=0&c=20201002) ,
,
and considering harmonic forcings and that
and that  is separable we get:
is separable we get:
The sole reason for including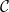 is to allow the possibility that
is to allow the possibility that 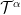 may be dependent on the type of forcing, e.g. WWMG, ice albedo, solar.
may be dependent on the type of forcing, e.g. WWMG, ice albedo, solar.
So I am saying that WMGGs produces a spatial pattern that is dependent on the angular frequency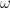 and that it may take complex values.
and that it may take complex values.
I understand you to be saying that for high vlaues of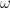 ,
,  is small overall due to heat storage and is comparatively biased towards the equator and away from the poles and for low values of
is small overall due to heat storage and is comparatively biased towards the equator and away from the poles and for low values of 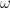 ,
,  is large overall and is comparatively biased towards the poles and away from the equator, and as
is large overall and is comparatively biased towards the poles and away from the equator, and as 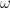 goes to infinity
goes to infinity 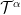 goes to its equilibrium distribution. Also that
goes to its equilibrium distribution. Also that  is large at the equator and small at the poles.
is large at the equator and small at the poles.
I will make the specific point that whereas I can see that the separation is plausible I cannot see this to be the case more generally. I.E.
is plausible I cannot see this to be the case more generally. I.E.  must be a sinusoid.
must be a sinusoid.
My analogue to![\beta_g \equiv [\mathcal{B} \mathcal{G}] \Rightarrow \mathcal{N} = \mathcal{F} -\beta_g [{T}]](https://s0.wp.com/latex.php?latex=%5Cbeta_g+%5Cequiv+%5B%5Cmathcal%7BB%7D+%5Cmathcal%7BG%7D%5D+%5CRightarrow+%5Cmathcal%7BN%7D+%3D+%5Cmathcal%7BF%7D+-%5Cbeta_g+%5B%7BT%7D%5D&bg=ffffff&fg=000&s=0&c=20201002) is not as straightforward as
is not as straightforward as ![[\mathcal{T^\alpha}]](https://s0.wp.com/latex.php?latex=%5B%5Cmathcal%7BT%5E%5Calpha%7D%5D&bg=ffffff&fg=000&s=0&c=20201002) is not normalised to unity as it contains information regarding the attenuation of amplitude with increasing frequency. So I would have (something like):
is not normalised to unity as it contains information regarding the attenuation of amplitude with increasing frequency. So I would have (something like):
That seems to have been a lot of fuss to show that in my way of thinking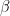 is a complex valued function of
is a complex valued function of 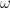 . So I do get your dependancy on frequency but that the functions being complex valued is not totally trivial.
. So I do get your dependancy on frequency but that the functions being complex valued is not totally trivial. 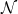 and
and 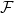 will not normally be in phase and
will not normally be in phase and 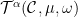 is not necessarily separable into
is not necessarily separable into  where
where  is real valued as the phase of
is real valued as the phase of 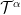 might vary with
might vary with 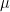 .
.
I am beginning to wonder if this was worth saying but it was good to practice a bit of Latex and I am not letting it go to waste. Anyway all my functions are linear and combining the spatial vectors for temperature and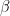 would give the required results.
would give the required results.
I did look at what would be needed to calculate the immediate radiative restoring strength and it must be just the integral of the product of the restoring vector and the Fourier transform of the forcing, but in practical terms that is as good as a useless thing to know.
Alex
Alex, the distinction is only that I am separating off the relationship between top-of atmosphere flux and surface temperature from the rest of the model, as this has no frequency dependence to speak of on the time scales being discussed here — since this connection is generated on atmospheric time scales (at most a couple of months). The slow physics can influence this relationship by changing spatial structure of the temperature response, so the relationship between spatial structure and forcing can have time lags, but the relation between this spatial structure and the energy balance does not (in this simple picture).
Isaac,
Sorry I was off on a tangent, trying to dig into the implications of your explanation after the your paragraph that starts:
“The story seems to be something like this:”
Returning to the main thrust. I spotted something that I found rather alarming and I checked Winton et al (2010) to make sure that it was recognized and it is:
“The stabilized forcing warming commitment inherent in a given level of ocean heat uptake is magnified by the efficacy.”
Given that the ocean heat uptake efficacy due to the current “experiment” in the real world is modelled to be ~2.5, the standard method Stored Flux {W/m^2} times Equilibrium Sensitivity {ºC/(W/m^2)} would only give ~40% of the implied value for committed warming, which is rather scary.
I have also looked at how the N/R – T/Teq curve would incorporate into a simple thermal model in terms of response functions and whereas it can be done easily enough I can not see how it can be constrained by real world data so it would have to rely on the simulated curves.
All in all, the prospect that the actual curve does lie below the linear approximation is not a pleasant one and I can see that it has many repercussions. Notably that empirical estimates for the sensitivity will tend to underestimate.
It is not clear to me how much of the apparent efficacy as T approaches Teq is due not to the effect you described but to slow feedbacks in the simulators e.g. ice albedo. I think the described effect should, provided that the warming is monotonic for all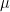 , lead the curve to finally reattach to the linear slope close to Teq whereas a slow feedback would not.
, lead the curve to finally reattach to the linear slope close to Teq whereas a slow feedback would not.
However if the warming were not monotonic but ended say with the poles warming whilst the equator cooled any final value of the slope would be a difference and its value would not be so restricted. It was that sort of worry that lead me to speculate on the effects of various differential warming patterns in my note above. Also it occurred to me that such warming patterns would give rise to continuing differential warming even if we could hold the global average temperate constant. As you inform us on other threads and your papers, small differentials are implicated in significant regional climate change, e.g. hurricanes and sahel rainfall patterns. That we cannot unrock the boat and that some patterns of differential warming are already committed too is not a benign notion.
If I have interpreted the main thrust correctly, it makes for gloomy reading, and I think that these consequences may not be as widely appreciated as they should be.
Alex
I am not sure that I follow everything that you are saying — but If we knew the forcing well enough, we could constrain long time scale responses with paleoclimates and faster responses with the observed warming over the past century, to see if we are getting the ratio of TCR to Teq about right. It’s a challenge. In any case, we need to clearly distinguish between the constraints on responses on different time scales and not just assume that these ratios are well known. if this picture is right, knowing the heat uptake is not enough to convert TCR into Teq
Sorry that am still not being clear (and in parts downright wrong).
I am trying to combine your insight into my thinking regarding simple models and I shall try a different tack.
The curve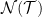 that represents the underlying trajectory of the simulator is also a function of
that represents the underlying trajectory of the simulator is also a function of 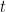 , the
, the 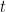 parameter increasing along the curve from top left to bottom right.
parameter increasing along the curve from top left to bottom right. 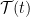 being the temperature response function for a step forcing.
being the temperature response function for a step forcing.
Let us say that it has an initial slope that is steeper than the curve so when extended as a straight line the curve is always above it. The curve could then be considered as the sum of this new line and an additional positive slow forcing of some sort
that is steeper than the curve so when extended as a straight line the curve is always above it. The curve could then be considered as the sum of this new line and an additional positive slow forcing of some sort  .
.
By slow forcing I mean one that cannot be represented as being proportional to the instantaneous value of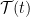 but the result of the historic values of
but the result of the historic values of 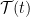 and represented by the convolution
and represented by the convolution  for some function
for some function 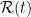 that captures the dependence on
that captures the dependence on  on the historical values. Provided the system is linear, I believe that this separation can always be achieved.
on the historical values. Provided the system is linear, I believe that this separation can always be achieved.
In that sense the curve can be seen as being due to a lower than equilibrium value sensitivity plus an additional (and perhaps somewhat fictitious) slow forcing.
Now I presumed that the GFDL model also contains some “genuine” slow feedback forcing e.g. albedo which evolves slowly and hence is not proportional to the current temperature but some function of the temperature history, that is how I view the difference between instantaneous (fast) and slow forcings.
So would be due to the combined effect of several distinguishable slow forcings, of which one would be due to the temporal evolution of spatial warming patterns you proposed.
would be due to the combined effect of several distinguishable slow forcings, of which one would be due to the temporal evolution of spatial warming patterns you proposed.
Let this spatial component be . In one sense this feels like a convenient “fiction” but I can not logically consider it to be any more fictitious than the lapse rate feedback which is also due to a spatial effect, the variation of warming with height. That said, the lapse rate feedback does differ in that it would be considered to be fast at these timescales.
. In one sense this feels like a convenient “fiction” but I can not logically consider it to be any more fictitious than the lapse rate feedback which is also due to a spatial effect, the variation of warming with height. That said, the lapse rate feedback does differ in that it would be considered to be fast at these timescales.
When I read your (Soden & Held) paper(s) that compared simulators by way of an analysis based on kernels, I did wonder whether such a spatial aspect could have been considered as it seemed likely to me that the simulators might have different equilibrium polar amplifications. This case differs that in that we are considering the whole trajectory so the evolution of the spatial pattern needs to be represented, but the justification for adding an additional spatial feedback would be the same and I think valid. That said it would require some redefinitions of the individual feedbacks, in particular changing the Planck feedback to represent its “initial” value which would be more negative than otherwise.
I shall try to make a case for this line of thinking. It is based on a consideration of what one might deduce about the restoring strength from short term (say sub decadal) observations of the flux imbalance.
According to my thinking, such an experiment would largely give a measure of the initial slope . Now in some of the literature this is at best considered to differ from the equilibrium slope only as a matter of the “real” slow forcings e.g. ice albedo etc.. Whereas it should also be corrected for the effects of the evolving spatial feedback due to
. Now in some of the literature this is at best considered to differ from the equilibrium slope only as a matter of the “real” slow forcings e.g. ice albedo etc.. Whereas it should also be corrected for the effects of the evolving spatial feedback due to  if the spatial signal is still evolving at this timescale (which I presume to be the case). By this I imply that failing to allow for this effect would result in too low a value for the equilibrium sensitivity.
if the spatial signal is still evolving at this timescale (which I presume to be the case). By this I imply that failing to allow for this effect would result in too low a value for the equilibrium sensitivity.
On a slightly different point, as I understand you, estimates of the restoring strength based on short term tropical data would lead to significantly lower values of equilibrium sensitivity for spatial reasons.
Even if I could never make a case for rejigging the feedbacks to this way of thinking; I do think that it has broadened my thinking on this topic substantially and hopefully not erroneously.
To my way of thinking, it does restrict the application of simple models when constrained only by the observational data. I do see your point about scale separation by use of both instrumental and reconstructed paleoclimatic data but I would now see the sequence to be for the simulators to be informed by the paleodata and for the emulators to be informed by the simulators, as is the case here. I do not see that the additional degree of freedom given by the curve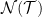 to a simple emulator can be adequately constrained by such a combination of centennial instrumental and millennial paleodata, as it can do no more than fix two points on the curve, so I feel that the production of candidate curves is best left to the simulators.
to a simple emulator can be adequately constrained by such a combination of centennial instrumental and millennial paleodata, as it can do no more than fix two points on the curve, so I feel that the production of candidate curves is best left to the simulators.
Thanks for this thread and your comments so far, they are appreciated and represent a very worthwhile learning opportunity, to me at least. I hope that by sticking to just a few points I have been more clear.
Alex
Hi Issac,
I was interested in your experiment to instantaneously double co2 and watch the system return to equilibrium. My test is to instantaneously add enough co2 to ultimately add 1C at equilibrium. Now I want to plot, U (“unrealized temperature increase”) = 1 – R (“realized temperature increase”) over time. What is the formula for U? If the recognition of temperature was proportional to the unrealized increase then this would simply be U = exp(-rt). From what I understand, due to the diffusive nature of conduction, “r” is not constant and diminishes over time. Can this formula be expressed as U=exp(f(t))?
The reason I ask is because the “heat in the pipeline” problem, in financial mathematics terms, looks like a future value of an annuity problem. If we regress ln(accumulated co2), we can get a good match with a second order polynomial. We then take the derivative to get a linear equation representing our rate of deposit into the unrealized account. If our “force of interest” were negative (withdrawals) and constant then there would come a point where the rate of deposit equaled the rate of withdrawal and our unrealized account would have hit an upper limit. Can a similar approach be used with a diminishing “r” to demonstrate that there is no upper limit in this scenario?
Thanks, AJ
There is the potential for thinking that one is closing in on an equilibrium, but then being surprised that slow processes continue to warm the system. But I don’t understand your concern about there being no upper limit. I am not very good at converting things like “force of interest” into an equation.
Dr. Held,
I’ve recently been looking over some of the outputs from GFDL CM2.1, and going over the Winton et al (2010) paper, so I was glad to see you had posted on this before. Forgive me if this is a dumb question, but I’ve been a bit stumped by something:
In Soden and Held (2006), the strength of radiative restoring appears to be -1.37 W/m^2/K for GFDL CM2.1, which when combined with the CO2 doubling 3.5 W/m^2 forcing (as shown in Winton et al for example) for this model would seem to indicate an equilibrium sensitivity of 3.5 / 1.37 = 2.55 K, which is a good deal different from the 3.4 K sensitivity we know for the GFDL CM2.1 model.
Do you suppose that this is because of the changing sensitivity described here, where Soden and Held (2006) uses only the first 100 years to calculate the radiative response to a temperature increase, which is stronger than in subsequent years (perhaps due to the differing spatial structures of the surface temperature change)? Or are there other factors (or some misunderstanding on my part) at work here?
Yes, that is the point I am trying to make here — the strength of radiative restoring, measured by global mean flux change per unit change in global mean temperature, does weaken as the system equilibrates.
Thank you for your blog posts. They are really a treasure for thinking about many important topics. Although I don’t really understand all of them, they are very enjoyable to read.
For this post, it seems that I could grasp the idea that high-low latitudinal contrast is arguably from the difference in atmosphere and ocean responses. Therefore, there’s slow and fast response time scales. However, for the ocean to realize this slow response, i.e. latent warming that is mixed into deeper ocean coming back to resurface, the time scale will be quite long, much longer than a few dozens of years, right?
Having read Andrews et al. 2014, Andrews et al. 2015 and Gregory and Andrews, 2016, their message seems to be that most of this nonlinear behavior of radiative restoring parameter comes from low latitude cloud feedback. Of course, they didn’t go into the depth explaining the reason for this SST pattern change.
Is there a fundamental difference between their view from what you proposed here?
I am not sure that I am up to date on all of these papers, but I think we are on the same page. Changes in cloud feedbacks may be the proximate cause of a change in radiative forcing with time, but tracing it back this change is presumably related to the pattern of SST change, as discussed by Armour and others. And then you can trace it back further to the changes in ocean heat uptake as controlling the pattern of surface temperature change, as Mike Winton has emphasized. I think this sort of thing would be easier to sort out if we looked at the response in the frequency domain more often, rather than just looking in the time domain, to get a sharper picture of the frequency-dependence of the radiative restoring and how it is controlled.
You have to be careful with the terminology different people use. When I use the term “fast” response, I am referring to the part that is fast compared to the evolution of anthropogenic forcing. This is not just due to the land response, but also includes the response of the oceanic surface mixed layers. The same term is used by others when discussing shorter time scales that are due primarily to the land (and atmospheric) responses that takes place before even the surface oceans have responded much. To paleoclimatologists the fast response might be everything short of the Greenland and Antarctic ice sheet response times.
Thank you for the clarification.
Indeed, the ocean heat uptake view may be philosophically more ‘fundamental’ while the direct feedback calculations give a more straightforward view.
I need to read both batches of papers to get a more in depth understanding.
On the point of the fast and slow, it’s well taken.